⾼等学校卒業程度認定試験(令和3年_数学)の解説
1.はじめに
海外の試験を観た時に試験範囲を除くと、大学の入試試験の難易度として、⾼等学校卒業程度認定試験は比較的妥当なレベルだと感じています。
入学を難しくするより卒業を難しくした方が良いと考えているためです。
イタリアのカターニア大学のプルチーノらによる「才能か運か」と題する論文を見ると、シュミレーションの結果、富める人々は幸運に恵まれた人々だったとのことです。
更に研究費の配分について最大の効率だったものは「すべての科学者に均等に研究費を配分する」ものでした。
これらが意味することは、何が当たるか分からないからとりあえずやってみなはれということだと思います。
私はこれは大学入試とも関係しているものだと思います。最低限の理解がある(大学の授業が分かりうる)レベルであれば、とりあえず入学してもらうことで、その中から優秀な成果をもたらす人も出るのではないかと考えています。
上記のように記載しましたが、私には大学の制度を変える力もないので、この記事は高卒認定を受けて大学に行きたいという人の助けになれば幸いです。
2.試験範囲(令和6年度から数学の範囲は変わりそう)
この記事では、過去問は現時点で令和3年までしか公開されていなかったので、令和3年第二回について解説します。
ちなみに著作権は問題ないです。
ガイドライン:文部科学省ウェブサイト利用規約(https://www.mext.go.jp/b_menu/1351168.htm)
令和4年度入学者から新しい学習指導要領に基づいた学習が実施されているため、令和6年の数学の試験は変わるものと思われます。

新課程の「数学I」は「数と式」に「有限小数、循環小数」が追加、「図形と計量」、「二次関数」、「データの分析」に「仮説検定の考え方」が追加となっています。
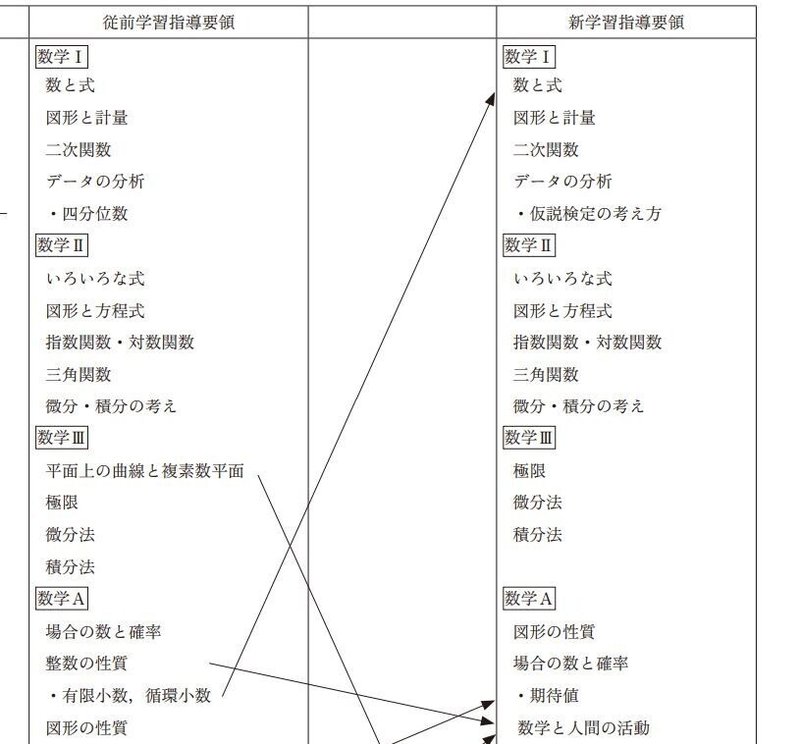
(https://www.mext.go.jp/content/20230217-mxt_kyoiku02-100002620_05.pdf)
問題が公表されたら確認しようと思いますが、「数と式」と「データの分析」に関して、数問は影響がありそうかなという感触です。
しばらく年数を開けて受験される方は、私が制度自体には詳しくないこともあるので、ホームページでご自身で確認されることをお勧めします。
3.問題解析
1.大問1(1)
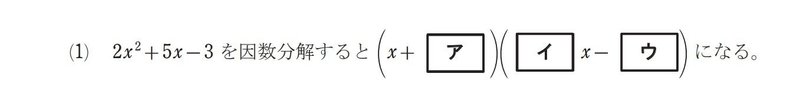
(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
まず因数分解できると何が嬉しいかというと、方程式で解を求めることができます。例えば 以下のような式があった場合、因数分解できるとx=3とx=2が解であることが分かります。
$${y=x^2-5x+6=(x-2)(x-3)}$$
今回の問題は、どのように因数分解するかという問題です。たすき掛けという方法を練習することをお勧めしますが、知らなくても以下のように解くこともできます。
因数分解後の形を展開して係数を比較します。
$${(x+ア)(イx-ウ)=イx^2-ウx+アイx-アウ=イx^2+(アイ-ウ)x-アウ}$$
まずxの2乗の係数は2なので、イは2になります。
そしてxの係数は5なので、 2アーウ は 5 になります。
定数項は係数は -3 なので、-アウは -3 となり、アウは3となります。
ここからは組み合わせを探します。アウは3なのでとりあえず
(ア,ウ)=(1,3),(3,1) 位が考えられそうです。
次に 2アーウ に上記の組み合わせを入れると(ア、ウ)=(3,1)が 5 になることが分かります。
したがってア=3,イ=2,ウ=1となります。
$${y=2x^2+5x-3=(x+3)(2x-1)}$$
[対策]
(数と式)たすき掛けの問題を解いて練習することをお勧めします。
2.大問1(2)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
展開が正しくできるかという問題です。
$${(a^2+b)^2=(a^2+b)(a^2+b)=a^2a^2+a^2b+ba^2+b^2}$$
$${=a^4+2a^2b+b^2}$$
よって回答は3番です。
慣れている方はもう少し省略して計算したり、2乗の展開の公式で計算されてもよいと思います。
公式忘れても、項をそれぞれかけ算すれば計算できることを示しています。
[対策]
(数と式)展開の問題を解いて練習することをお勧めします。
3.大問1(3)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
集合に関する問題ですが、言葉と記号の意味を覚えていないと辛いと思います。
問の{1,3}という集合は、集合 A と集合 B の共通部分(AにもBにも含まれる)です。よって 「AかつB」となります。
$${A \cap B}$$
答えは2番です。
[対策]
(数と式)集合について記号とその意味を復習することをお勧めします。
4.大問2(1)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
一次不等式の問題です。不等号が逆転するのは-の数を掛けた時(割った時)です。納得できない人のために一旦具体例を見てみます。
-2を掛けた場合の具体例を見てみます。
①両辺が正の数の時、3<4 (-2)を掛けると -6>-8
➁片方が負の数の時、-3<4 (-2)を掛けると 6>-8
➂両辺が負の数の時、-4<-3 (-2)を掛けると 8>6
問題を見ると①は5を足して不等号が逆転していますが、そうはなりません。
➁は正の数である3分の1がかかって不等号が逆転していますがそうはなりません。
➂は正の数2がかかって、3を引いていますがこれも不等号は逆転しません。
④はマイナスの数(-4)がかかっているので逆転します。
したがって答えは④です。
[対策]
(数と式)一次不等式を勉強してもらえればと思いますが、マイナスの数を掛けているか割っているかだけ注目すれば、この問題は解けるかなと思います。「数と式」には「有限小数、循環小数」が加わるので、もう一問位傾向が変わりそうかなと思います。
5.大問2(2)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
中学で方程式を立てるのが苦手だった人は少し苦戦するかもしれません。
この問題はまず以下の関係性を見抜くところにあります。
(部数)×(一部あたりの印刷費)=(印刷費)≦(予算)
次に印刷費が1000部までで変わることに注目します。
この後で分からない数をxと置いて式を立てますが、以下の2つの考え方の内考えやすい方で良いかなと思います。
①1000部を超えた印刷部数をxと置き、以下のように解きます。
$${1000×15+x×12 \leqq 30000}$$
$${x×12 \leqq 15000}$$
$${x \leqq 1250}$$
xは最大で1250部であることが分かったので、最大印刷部数は1000+1250=2250 部となります。
(最初の 1000 部を忘れないようにする必要があります。)
➁最大印刷部数をxと置きます。この時、1000部は15円で、(x-1000)部が12円であることに注意します。
$${1000×15+(x-1000)×12 \leqq 30000}$$
$${15000+12x-12000) \leqq 30000}$$
$${12x \leqq 27000}$$
$${x \leqq 2250}$$
最大印刷部数は2250 部(イウエオ)となります。
[対策]
こういった問題が苦手な場合は関係性を見抜くことが苦手な場合があります。中学の方程式の問題も利用して立式する練習が必要かと思います。
6.大問3(1)
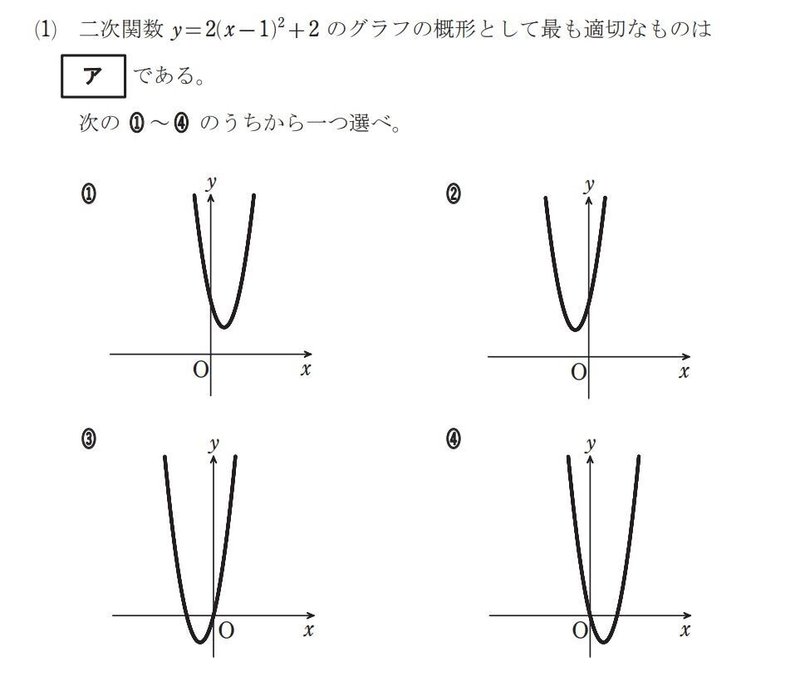
(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
まずは二次関数のxの2乗の項の係数に注目して、上に凸か下に凸かを確認します。下の図のようになります。
・xの2乗の項の係数が正の時:下に凸
・xの2乗の項の係数が負の時:上に凸
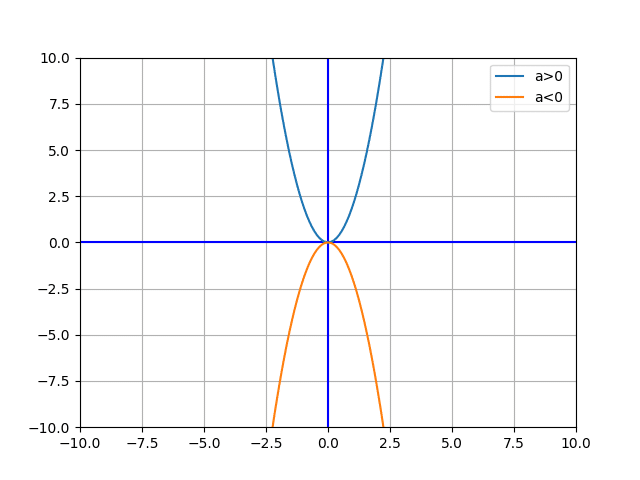
次にグラフの平行移動について考えます。
$${y=2x^2}$$ [1]をx方向に+2移動させたもの[2]と、x方向に +2、y方向に +2移動させたもの[3]を以下に示します。
[2]:$${y=2(x-2)^2}$$
[3]:$${y-2=2(x-2)^2}$$
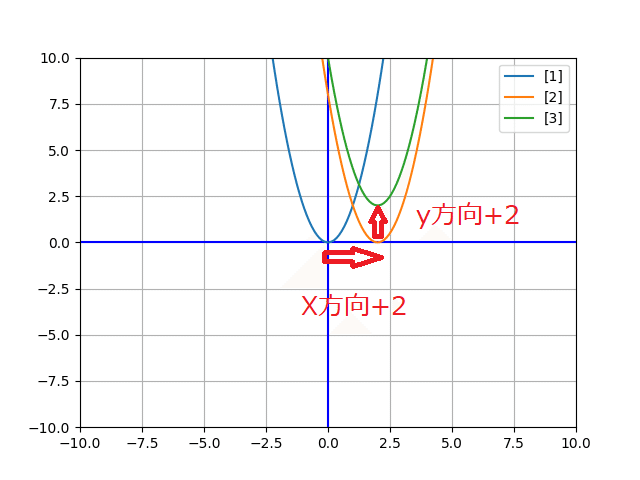
つまり $${y=ax^2}$$ を x方向にp、y方向にq平行移動させると、
$${y-q=a(x-p)^2}$$ または $${y=a(x-p)^2+q}$$ という関数になります。
ちなみに頂点(出っ張ってる先)は(0,0)から(p,q)になります。
では上記の基礎知識を踏まえて問題を解きます。
$${y=2(x-1)^2+2}$$ は下に凸で頂点が(1,2) となる二次関数です。
よってアは①となります。
7.大問3(2)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
頂点が(1,1)なので、$${y=a(x-1)^2+1}$$ とおけます。
これが(0,-2)を通るので値を代入します。
$${a(0-1)^2+1=-2}$$
$${a+1=-2}$$
$${a=-3}$$
したがって$${y=-3(x-1)^2+1}$$
イの答えは➂になります。
8.大問3(3)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
二次関数を$${y=a(x-p)^2+q}$$の形にすることを平方完成といいます。
問題より難しい$${y=2x^2+4x-9}$$を例に手順を示します。
① xを含む項を、x2の係数でまとめる。
$${y=2(x^2+2x)-9}$$
➁ xの係数を半分にして、2乗の形にして余計な数処理する。
xの係数が現在 2 なので、(x+1) の2乗にする。
すると(x+1) の2乗の定数項の数(1)に x2 の係数(2)をかけたものが邪魔な値として出てくる:1×2
その邪魔な値を引く。
$${y=2(x+1)^2-2-9}$$
$${y=2(x+1)^2-11}$$
これは$${y=2x^2}$$を x方向に -1、y方向に-11移動したものであることが分かります。
手順を確認したところで問題を解きます。
$${y=x^2-6x+16}$$ はx2の係数が1なので、手順➁から実行します。
xの係数が現在 -6 なので、半分を考え(x-3) の2乗にする。
定数項の数 9 が邪魔になるので引くという流れになります。
$${y=(x-3)^2-9+16}$$
$${y=(x-3)^2+7}$$
したがって頂点は(3,7)になります。
よってウは3,エは7になります。
[対策]
二次関数、二次方程式、二次不等式は平方完成がメインです。これさえできればグラフが書けます。さらに解の公式が無くても解を求めることができます。(大問4の(2)で説明します。)ですから平方完成してグラフさえ書けばほとんど解けると考えてよいです。
9.大問4
(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
全て平方完成してグラフを書くという方針で解けます。
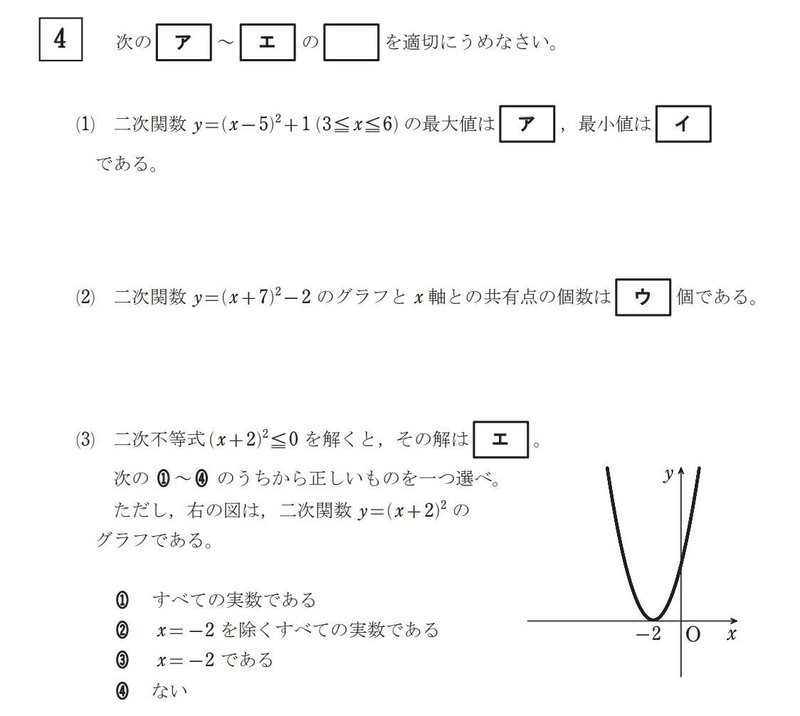
(1)既に平方完成済なので、頂点が(5,1)で下に凸なグラフであることがわかります。

グラフより最大値は x=3の時なので、以下のようになります。
$${y=(3-5)^2+1=(-2)^2+1=5}$$
したがってアは 5 となります。
また最小値は頂点なので、イは1となります。
(2)既に平方完成済なので、頂点が(-7,-2)で下に凸なグラフであることがわかります。
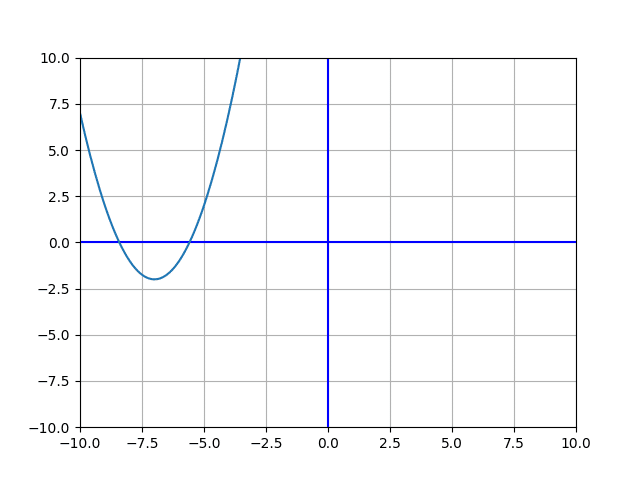
x軸との共有点は2個なので、ウは2個になります。
ちなみにy=0となる xの値、すなわち解を求めよと言われた場合、次のように計算できます。解の公式を覚えなくても平方完成で解が求めることができるということを説明しました。
$${(x+7)^2-2=0}$$
$${(x+7)^2=2}$$
$${(x+7)= \pm \sqrt{2}}$$
$${x=-7 \pm \sqrt{2}}$$
(3)(x+2) の2乗をy=とすると、問題に書かれている図のようになります。
引っかかりやすいのは、y≦0 というところで、y=0 も条件を満たすので、まず x=-2 が条件を満たすことが分かります。
次にその他のx では y>0 となっています。
したがって解はx=-2 のみなので、エは➂となります。
10.大問5(1)(2)
(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
三角比は角度から線を求めたり、線から角度を求めたりすることができる優れた測量術です。
中学生でやった相似や三平方の定理から、直角三角形と各辺の長さで比を作って三角比の表を作っています。
まず三角比の定義を表示します。
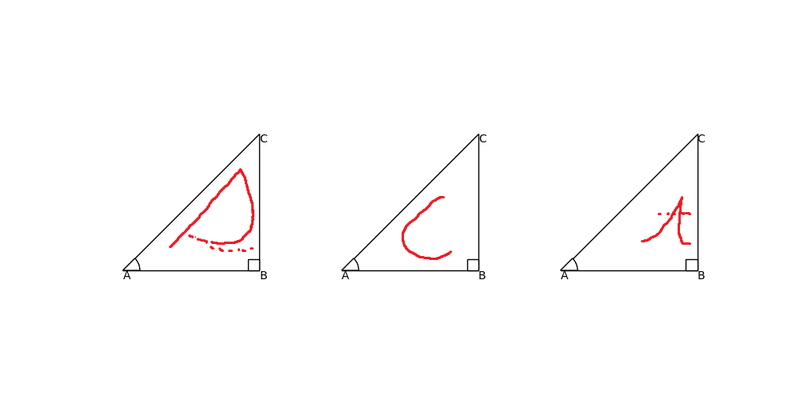
$${\sin ∠A=\frac{BC}{AC}}$$ [筆記体のsで覚えてください]
$${\cos ∠A=\frac{AB}{AC}}$$ [筆記体のcで覚えてください]
$${\tan ∠A=\frac{BC}{AB}}$$ [筆記体のtで覚えてください]
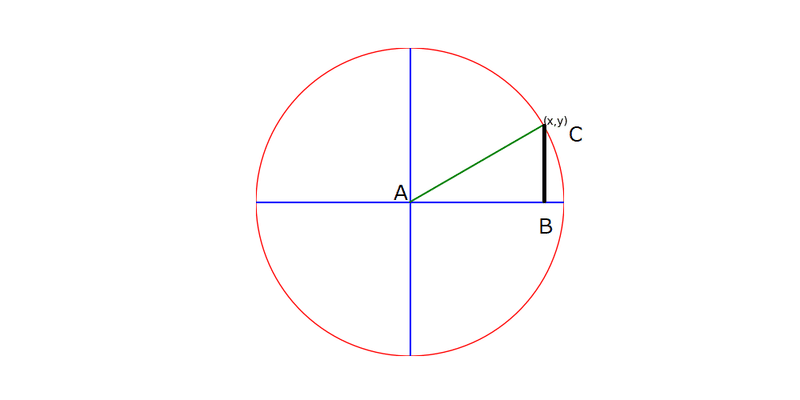
単位円(半径1の円)で三角比を考えると以下のようになり、AC=1なので、BC が y座標の値、AB がx座標の値と一致することが分かります。
したがって sin∠A=(y座標の値)、cos∠A=(x座標の値)、
tan∠A=(y座標の値)/(x座標の値) となります。
このように考えると90°を超えた角についても三角比を定義することができます。
また以下の式が成立します。
・三平方の定理より $${x^2+y^2=1}$$
$${\sin^2x + \cos^2 x=1 }$$
・$${\tan x= \frac{y}{x}= \frac{ \ sinx}{ \ cosx}}$$
90°を超えた角については、90°以下に変更できる関係式があります。
以下の図から、θ座標を(x,y)とすると、180-θの座標は(-x,y)であることが分かります。(θはとある角度のこと)
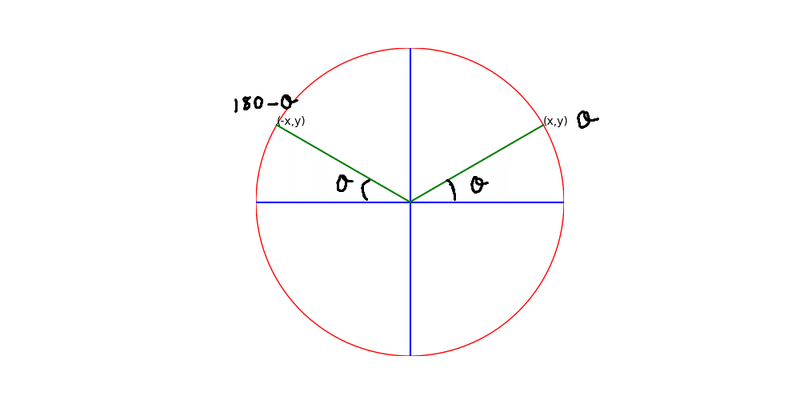
$${\sin(180-θ) = \sin θ}$$
$${\cos(180-θ) = -\cos θ}$$
$${\tan(180-θ) = -\tan θ}$$
ここまでの内容を把握したうえで問題を解いていきます。
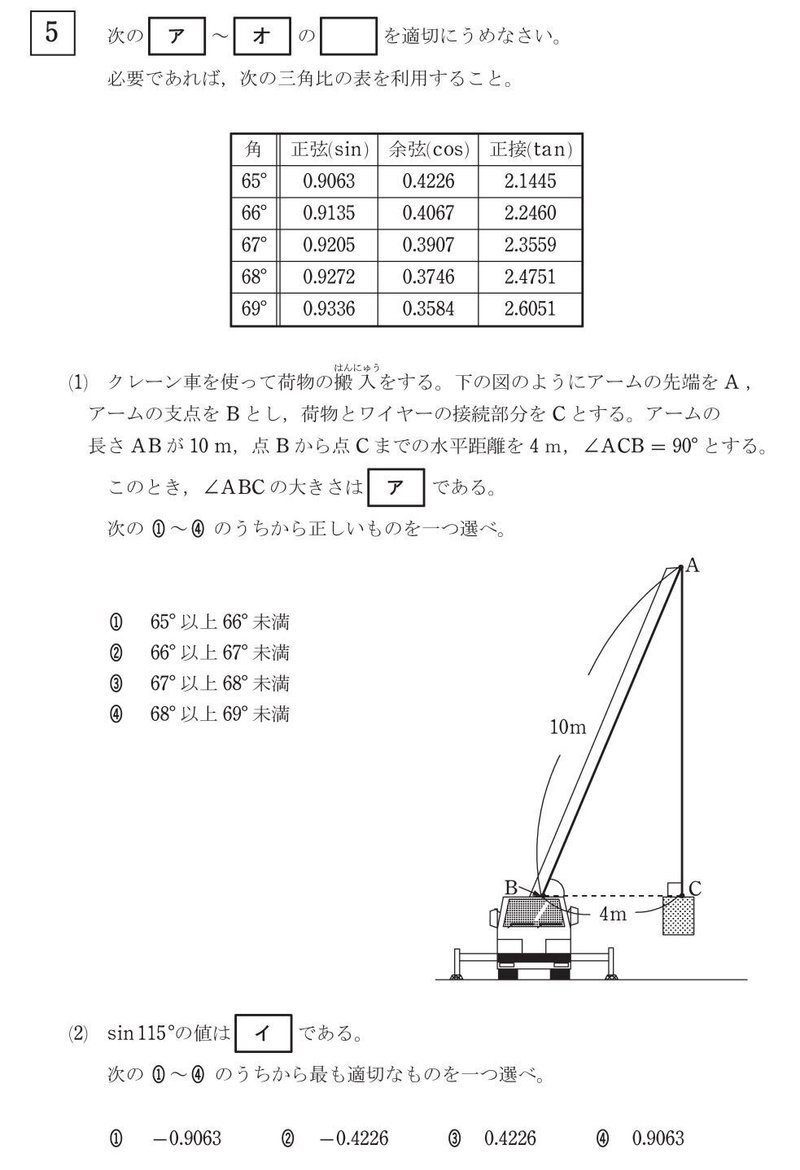
(1)線の長さがいくつか分かっている三角形の角度を求めるということで三角比を使用します。
まず∠ABC の sin , cos , tan を考えてみます。
すると cos∠ABC については二つの辺が分かっているので求めることができます。
$${\cos∠ABC=\frac{BC}{AB}=\frac{4}{10}=0.4}$$
三角比の表を見ると 66°と67° の間なので、アは➁になります。
(2)90°を超えているので180-θの関係式と三角比の表を使います。
$${\sin 115=\sin (180-65)=\sin 65=0.9063}$$
したがってイは④となります。
11.大問5(3)(4)(5)
(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
(3)90°を超えているので180-θの関係式を使います。
$${\cos^2 150=[\cos(180-30)]^2=(-\cos 30)^2=\cos^2 30}$$
したがって $${\sin^2 30+ \cos^2 30=1}$$ (なぜならば $${\sin^2x + \cos^2 x=1 }$$)
ウは1である。
正弦定理は以下の様な関係式です。辺と相対する角の関係性を示します。
$${\frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AB}{sinC}=2R}$$
R:内接円の半径
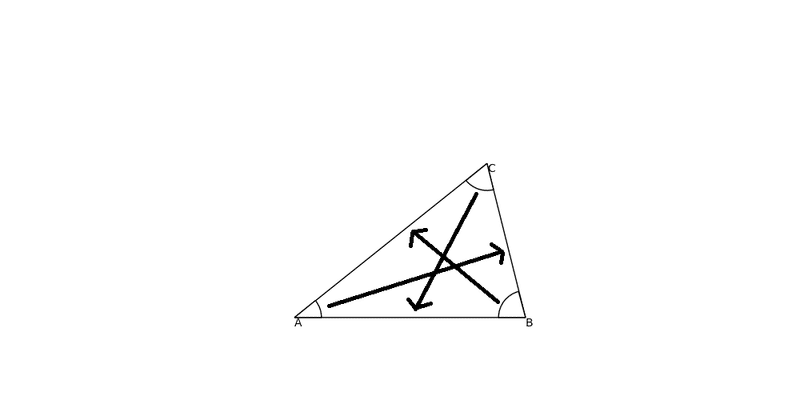
余弦定理は以下の様な関係式です。二辺とその間の角の関係性を示します。
$${BC^2=AB^2+AC^2-2・AB・AC・cos A}$$

直角三角形以外で辺と角度を求めるときに使用しますが、とりあえずは計算が簡単な正弦定理でできそうか見てみて、ダメなら余弦定理みたいなやり方でいいと思います。
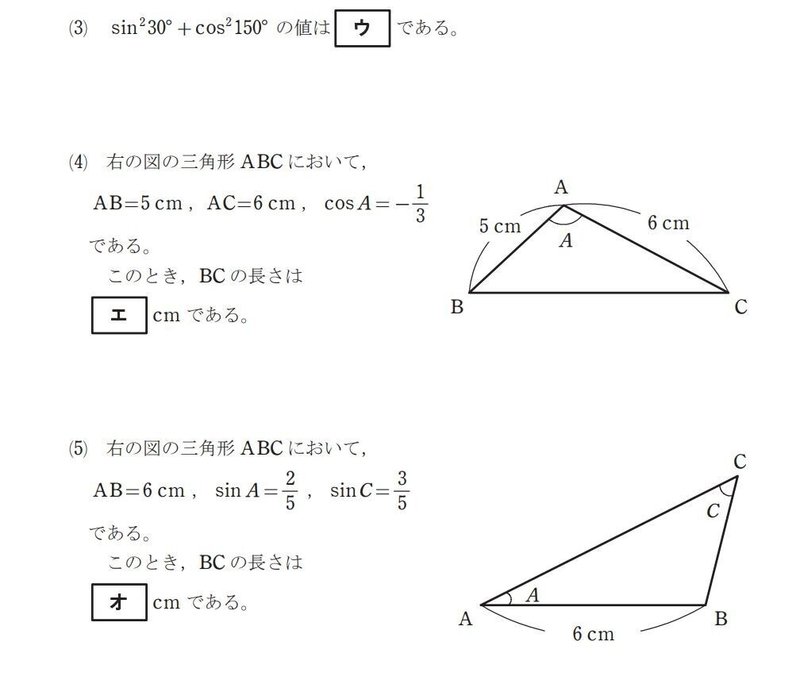
(4)求めたい BC と cos A が分かっているので、正弦定理が一瞬できそうですが、sin B も sin C も分からないので等式が立てられなそうです。
そこで余弦定理で解きます。
$${BC^2=AB^2+AC^2-2・AB・AC・cos A=5^2+6^2-2・5・6・(-\frac{1}{3})}$$
$${BC^2=81}$$
BC は辺の長さで正の値なので 9。エは9となります。
(5)正弦定理を使います。
$${\frac{BC}{sinA}=\frac{AB}{sinc}}$$
$${BC=\frac{AB・sinA}{sinc}=6×\frac{2}{5} ÷ \frac{3}{5}=6×\frac{2}{5} × \frac{5}{3}=4}$$
BC は 4 なので、オは4となります。
[対策]
図形問題は苦手意識がある人も多いと思いますが、三角比の基礎問題を練習して、当日は色々試しながら解くのがよいかと思います。
幸い似た形式が多いので、過去問を解いていく中でどれを使えばよいかも見えてくると思います。
12.大問6(1)(2)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
データのちらばりを評価する問題です。
範囲とは最大値と最小値の差を計算したものです。
データを小さい順に並べて、小さい順から数えてデータ数の1/4番目のデータを第1四分位数、2/4番目のデータを第2四分位数(中央値)、3/4番目のデータを第3四分位数といいます。
箱ひげ図は範囲と四分位数の値に横線を引いたもので、最小値、第1四分位数、中央値、第3四分位数、最大値について横線が引かれています。
それではそれぞれの問題について解説します。
(1)数を小さい順で並べます。(10個データがあるか確認しておきましょう)
1 / 1 / 2 / 2 / 3 / 3 / 4 / 4 / 5 / 6
まず中央値を探すために、小さい方と大きい方から一個ずつ数をチェックしています。すると 3/3まできます。そして中央値は 3/3 の値の中央、つまり (3+3)/2 で求めることができます。
よって中央値=3
1/1/2/2 3/<中央値:3>/3 4/4/5/6
次に第一四分位数を求めます。最小値と中央値までのデータの中央の値が第一四分位数となります。チェックしていく際には中央値は除きます。
1/1/2/2/3/<中央値:3>
すると2が中央の値であることが分かります。そのためアは2になります。
次に範囲は 最大値:6、最小値:1なので6-1=5。そのためイは5になります。
(2)数を小さい順に並べます。(9個データがあるか確認しておきましょう)
14 / 15 / 17 / 18 / 20 / 22 / 23 / 25 / 27
まず中央値を探すために、小さい方と大きい方から一個ずつ数をチェックしています。
すると 20 が中央の値になっていることが分かりますので中央値は20です。
次に第一四分位数を探します。すると 15 と 17 の間に中間があるので、第一四分位数は (15+17)/2=16 となります。
14 / 15 / 17 / 18 / <中央値:20>
次に第三四分位数を探します。すると 23 と 25 の間に中間があるので、第三四分位数は (23+25)/2=24 となります。
<中央値:20> / 22 / 23 / 25 / 27
つまり最小値:14、第一四分位数:16、中央値:20、第三四分位数:24、最大値:27 に横棒がある箱ひげ図を探すことになります。
➁:中央値 18 なのでおかしい
➂:第三四分位数が24ではない
④:最大値が27ではない
よってウは①となります。
[対策]
四分位数や箱ひげ図は考え方はシンプルなので、何問か練習して直前に復習して思い出すくらいでも解ける問題かなと思います。
データが偶数個の時と奇数個の時についてそれぞれ練習するようにしてください。
13.大問6(3)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
平均値とはデータを全部足して、その合計値をデータの数で割ったものです。
分散は平均値とそれぞれのデータの差の2乗を足したのちに、データの数で割ったものです。
計算式が問題文に乗ってはいましたが、事前に知識として持っておいたほうがいいと思います。
それぞれのデータの値が平均値に近ければ、値は平均値付近に集まります。
つまりデータは散らばっていないことになります。
逆にデータが散らばるというときは、平均値とデータの値が大きく異なるはずです。
そのため(データの値ー平均値)を足していき、値が大きくなればデータ全体として散らばっていそうだなということは何となく感じられるかなと思います。
ただ例えば平均値が3で、ある2つのデータが5と1だとします。これを単純に計算すると (5-3)+(1-3)=2-2=0 となり、データが平均値と同じだったように計算できてしまいます。
そのため 2 乗にしています。
さらにデータ数が多ければ、このずれの合計値はひたすら大きくなってしまうので、データ数で割っています。
それでは問題の解説をしますが、やることはシンプルなのですが計算量が多いので一旦他の問題を解くという方法もありだとは思います。
①平均値を求める。
・アブラゼミ
(4+2+6+2+4+2+1)/7=21/7=3
・クマゼミ
(2+3+2+5+4+3+2)/7=21/7=3
➁(データ-平均)、(データ-平均)の2乗をそれぞれのデータについて計算する。
・アブラゼミ
データ :4、 2、6、 2、4、 2、1
(データ-平均) :1、ー1、3、ー1、1、ー1、ー2
(データ-平均)の2乗:1、 1、9、 1、1、 1、4
・クマゼミ
データ : 2、3、 2、5、4、3、2
(データ-平均) :ー1、0、ー1、2、1、0、ー1
(データ-平均)の2乗: 1、0、 1、4、1、0、1
➂分散を計算する。
・アブラゼミ
(1+1+9+1+1+1+4)/7=18/7=2.5
・クマゼミ
(1+0+1+4+1+0+1)/7=8/7=1.1
計算の結果、平均値は同じで分散はアブラゼミの方が大きいことが分かります。
したがってエは➁
14.大問6(4)

(https://www.mext.go.jp/content/20230427-mxt_syogai02-mext_1411255_08sugaku.pdf)
[解説]
相関係数とは、2 種類のデータの関係を示す指標です。
値が 1 や -1 までの値を取り、0 に近いほど相関が弱いといえます。
そして プラスの値はあるデータが増えれば、もう一方も増えるという関係性を表し、マイナスの値はあるデータが増えれば、もう一方のデータは減るという関係性があります。
問題のデータは、「年間平均気温」と「年間積雪日数」となります。
「年間平均気温」が上昇すると「年間積雪日数」は減っているように見えます。
そのためマイナスの値となり、かつ明らかに傾向があるので1に近い値を取ります。
そのためオは「-0.85」の①となります。
[対策]
相関係数を求めるには、共分散をそれぞれの変数の標準偏差で割ります。式や計算等一度は体感してみると良いと思います。今回説明した内容だけでも結構解けると思いますが、仮説検定の問題が入るのかなと思います。
4.お勧めの書籍
非常に分かりやすい書籍です。
(数学Aの範囲は本試験に関してはやらなくてもよいです。)
以下の本も難易度的にお勧めです。
この記事が気に入ったらサポートをしてみませんか?
