昔、人に頼まれて競馬のオッズから買い目を計算するアプリを開発しました。各馬のオッズから計算した得票率の偏りに基づいて、そのレースが本命か波乱かの度合いや主に票を集め軸馬候補となっている馬が何頭居るか、それらの時間変化といった情報から買い目を計算します。自動でWebから情報を取ってきてHTMLをパースして必要なデータを集め、怪しい馬にマークをつけるというものです。

この買い目の計算過程で、各馬の得票率の偏りの具合を画一的に計算する方法、つまり集中度指標が必要でした。集中度指標には相対的集中度指標と絶対的集中度指標があり、それぞれ何種類かが経済学や統計学などの分野で用いられています。

中でも相対的集中度指標としてジニ係数が、絶対的集中度指標としてハーフィンダール・ハーシュマン指数が有名なのではないでしょうか。

ここで重要となるのがローレンツ曲線です。ここでは、事象の相対累積度数に対する頻度の相対累積度数の変化をローレンツ曲線とします。

買い目の計算アルゴリズムを設計している段階で、この用途に既存の絶対的集中度指標を使うには幾つかの問題点があることに気づきました。そこで、無いなら作っちまえのDIY精神で、絶対的集中度指標を自作しました。

統計を見てじゃあ結局どうなの? という事を直観的に理解できればこそ実用的です。中学生当時の思いつきではありますが、今更ながら基幹統計の問題が連日話題になっているので便乗して書いてみようと思います。

＊＊＊

統計データのローレンツ曲線を眺めていると、相転移の生じている位置(臨界点)が知りたくなります。臨界点が分かればそれに基づいた集中度指標を考えることができると思います。

しかしながらグラフからその位置を読み取って人力で臨界点を見つけるのはクールではありません。そこで数理的に求める方法を考えました。

まず、臨界点が一つの三角形のローレンツ曲線モデルを考えます。このモデルに当てはめて考えることで、ある種の集中度指標として画一的な表現が可能になります。

グラフのx軸は事象の相対累積度数、y軸は頻度の相対累積度数とします。

このローレンツ曲線モデルに於いて臨界点は三角形の頂点の位置です。ここが不平等の境目となります。

相対的集中度指標として有名なジニ係数は、幾何的に三角形の頂点の高さ即ち対角線からの逸れの大きさを表します。そのため臨界点が対角線と平行な線上を移動する限り値は変化しません。相対的集中度指標は、事象間の相対頻度の不平等の大きさを表しています。

ジニ係数は以下の式で求められます。

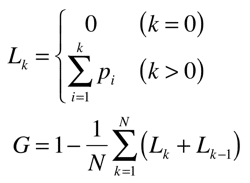
ただし、Nは事象数、L_kはローレンツ曲線、p_i={p_1,p_2,...,p_N}は昇順にソートした相対頻度とします。

ところで、絶対的にどれだけの事象に頻度が集中しているかを表すには、絶対的集中度指標が用いられます。ハーフィンダール・ハーシュマン指数(HHI)などが有名です。

しかしこれらの絶対的集中度指標は「絶対的にどれだけの事象に頻度が集中しているか」を感覚的にわかり易い値として表すことができません。ほとんどの絶対的集中度指標は相対的集中に対する感度も同時に併せ持ち、数値的に非線形な応答を示すので絶対的集中が「どの程度か」という量的な感覚に対して直観的ではありません。

そこで、このローレンツ曲線モデルに於ける臨界点が事象の累積相対度数(x軸)のどの位置に来るかを計算することにより、絶対的集中度指標として直観的な数値で表現できるように工夫します。

以下の式により臨界点のx軸の位置Vを求めます。

このとき、臨界点の座標(x,y)は以下のように求まります。

臨界点のx軸の位置Vとジニ係数Gから、新たに直観的な絶対的集中度指標µと相対頻度の不平等の度合いλを計算します。µは臨界点の累積度数(x軸に関係する成分)を表し、λは原点と臨界点を通る直線の傾きの度合い(y軸に関係する成分)を表します。すなわち「絶対的にどれだけの事象にどの程度頻度が集中しているか」を的確に表現します。

また、G,V,µから、臨界点を境に上層の代表的な相対頻度φ_Hと下層の代表的な相対頻度φ_Lも計算できます。

頻度の総和をsとした時、これらの数値を用いて例えば「N人中上位µ人にλ[%]の集中度があり、代表的な頻度は上層がsφ_Hで下層はsφ_Lである」という形で画一的で直観的な表現が可能になります。

競馬に当てはめるならば「N頭中上位µ頭にλ[%]の票の集中度があり、代表的な得票率は人気層がφ_H[%]で不人気層はφ_L[%]である」のように表現できます。φ_Hが大きいと軸馬に対する期待度が大きく、φ_Lが大きいと対抗馬が多く寡占状態であることがわかります。競馬市場は一般的にその馬の得票率が勝率に近い効率的市場なので、集中度指標からレースが波乱か本命か、馬券の式別による心理的バイアスのかかり具合などが読み取れ、効率的な馬券の購入を提案することができます。

＊＊＊

Vを求めるにあたって前もってGの計算が必要となりますが、計算アルゴリズムとしてVとGを一緒にまとめて効率的に計算する方法を考えます。

式を以下のように変形します。

以下にC言語による簡単な実装例を示します。

double getConcentrationIndex(double *g, double *v, double p[], size_t n) {
    double s = 0.0, u = 0.0, w = 0.0;
    for (size_t i = 0; i < n; i++) {
        double t = (double)(i + 1) / n;
        
        u += s + s + p[i];
        s += p[i];
        w += t * (t - s);
    }
    
    *g = 1.0 - u / n;
    *v = 6.0 * w / (n - u) - 1.0;
    
    return s;
}

＊＊＊

以上のように、ローレンツ曲線モデルに於いて振る舞いが明らかなG,Vを用いることで工夫次第でµ,λのような集中度指標やφ_H,φ_Lのような代表的な値の指標がイメージし易い形で設計できます。

ローレンツ曲線モデルを想定しその臨界点を求めることで、集中度指標を設計するための方法論を確立しました。優れた指標は全体の様子を量的感覚として直観的に表現できる指標であると考えます。これを応用して様々な用途に合った優れた指標を作成できれば良いと考えています。

参考文献
計量書誌学的分布における集中度 : 指標の感度と標本量依存性
http://www.slis.tsukuba.ac.jp/~yoshikane.fuyuki.gt/jslis_00s_yoshikane.pdf

#集中度指標 #ローレンツ曲線 #統計 #DIY