
繋がりを可視化する グラフ理論入門
個人的に、一番面白いデータ構造であり探索アルゴリズムです。
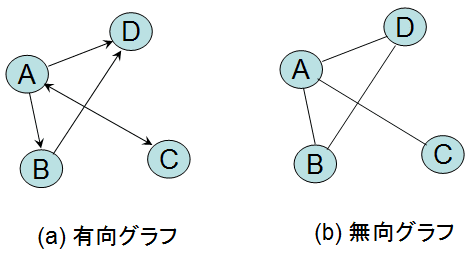
ここで言うグラフは円グラフや、棒グラフのことではないです。プログラミングで扱うのは、図のように、点と線を繋げたものです。

ズバリ、人と人の繋がりを表現できます。
今回もJavascriptで実装します。
グラフ理論は、SNSだったり、レコメンドだったり、地図の経路だったり ルーティングだったり、点と点の繋がりを可視化します。繋がりを表現するデータ構造です。
巨大なインターネットもそうです。
そいう意味で、すごく身近なアルゴリズムですよ。
グラフの基本は次の2点で構成されています。
・ノード:node(vertex) - 点(人、物、場所)
・エッジ:edge - 辺(繋がり、経路)

上の図を見ると一目瞭然ですね。ノードを人だとしたら、エッジが関係性です。まずは、これだけ理解できれば大丈夫です。
ちなみに、方向がない辺を無向グラフ、矢印がある一方な辺を、有向グラフと言います。SNSの例がわかりやすいですね。facebookだと、友達承認されるとお互いが、繋がります。一方でtwitterは一方向からフォローになります。
有向グラフ:インスタグラム、twitter
無向グラフ: facebook
以下がコードです。
グラフ を表現する。
今回は、グラフをハッシュテーブルで、管理していきます。各ノードをキーバリューペアで、繋げたいノードと対応させていきます。下の例だとノード「A」は「B」と「F」と繋がっています。

早速実装してみましょう。まずはグラフのコンストラクタ。全てをadjacencyListに格納していきます。
class Graph {
constructor() {
this.adjacencyList = {};
}
}ノードを追加するメソッドを作成します。vertexがノードです。ハッシュマップのキーになります。
addVertex(vertex) {
this.adjacencyList[vertex] = [];
}次に、ノード同士を繋ぐメソッドを作成します。これがエッジ(辺)を表現します。対応するキーの配列にpushしていきます。注目して欲しいのは、v1に対してv2が繋がり、その逆も繋げていますね。つまり双方向(無向グラフ)です。
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2);
this.adjacencyList[v2].push(v1);
}※ちなみに有向グラフにしたければ、片側だけpushすればOKです。
エッジを削除するメソッドです。filterメソッドで、ノードを取り除いた配列を返します。これも両側の関係を解消するので、お互い対応した処理が必要です。
removeEdge(vertex1, vertex2) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
v => v !== vertex2
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
v => v !== vertex1
);
}ノードを削除するメソッドです。まず先ほどのremoveEdgeで削除したい、ノードのエッジを解消していきます。最後にdeleteでキーごと削除します。
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex];
}グラフ(データ構造)最終版
class Graph {
constructor() {
this.adjacencyList = {};
}
//ノード追加
addVertex(vertex) {
this.adjacencyList[vertex] = [];
}
//無向グラフ
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2);
this.adjacencyList[v2].push(v1);
}
//有向グラフ
addEdgeDirected(v1, v2) {
this.adjacencyList[v1].push(v2);
}
//エッジを削除
removeEdge(vertex1, vertex2) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
v => v !== vertex2
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
v => v !== vertex1
);
}
//ノードを削除
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex];
}
}ノードとエッジの設定
let graph = new Graph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addVertex("E");
graph.addVertex("F");
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("B", "D");
graph.addEdge("C", "E");
graph.addEdge("D", "E");
graph.addEdge("D", "F");
graph.addEdge("E", "F");
// A
// / \
// B C
// | |
// D --- E
// \ /
// F
console.log(graph);実行結果
>node graph.js
Graph {
adjacencyList:
{ A: [ 'B', 'C' ],
B: [ 'A', 'D' ],
C: [ 'A', 'E' ],
D: [ 'B', 'E', 'F' ],
E: [ 'C', 'D', 'F' ],
F: [ 'D', 'E' ] } }グラフを探索する。
ここから面白くなって来ます。いよいよグラフを探索していきます。
P2Pネットワーク、Webクローラー、レコメンド、最短距離。全部グラフの探索です。
今回は深さ優先探索と幅優先探索というアルゴリズムを使います。何が違うのかというと、ノードを探索する順番が変わってきます。深さ優先探索はひたすら、次のノードを探索します。一方で、幅優先探索は開始ノードに近い順に探索します。
深さ優先探索:「とにかく行けるとこまで行ってそれ以上進めなくなったら一歩戻ってそこから探索する」
幅優先探索:「出発点に近い点から順に探索する」
例
// A
// / \
// B C
// | |
// D --- E
// \ /
// F
深さ優先探索 A→C→E→F→D→B
幅優先探索 A→B→C→D→E→Fポイントは、一度訪れたノードにはフラグを立てて記憶しておくこです。
深さ優先探索(DFS)
depthFirstIterative(start) {
//ノードを格納するスタック
const stack = [start];
//訪れた順番を格納
const result = [];
//訪れたフラグ
const visited = {};
//現在のノード
let currentVertex;
//訪問済みフラグを立てる
visited[start] = true;
while (stack.length) {
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
});
}
return result;
}順に追っていきましょう。使用するデータは以下adjacencyListです。
adjacencyList
{ A: [ 'B', 'C' ],
B: [ 'A', 'D' ],
C: [ 'A', 'E' ],
D: [ 'B', 'E', 'F' ],
E: [ 'C', 'D', 'F' ],
F: [ 'D', 'E' ] } }// A
// / \
// B C
// | |
// D --- E
// \ /
// FノードAから開始する。
ノードAは訪れたのでvisitedとマーク。
stackには、ノードAがあるのでwhileが回る → stack[A] result[]
stackからpop。Aを取り出してresultにpush。 → stack[] result[A]
Aをforeachでループ。BとCを取り出す。
BとCは訪れていないのでフラグを立てる。
BとCの順にstackにpush → stack[B,C] result[A]
whileの先頭にくる。stackからCをpop → stack[B] result[A,C]
Cに紐づくA,Eを取り出す。Aは訪れたので、Eをスタックにpushす。(重要:EはBの上になる)→ stack[B,E] result[A,C]
以後、繰り返し。
実行結果
>node graph.js
[ 'A', 'C', 'E', 'F', 'D', 'B' ]
幅優先探索(BFS)
breadthFirst(start) {
const queue = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while (queue.length) {
currentVertex = queue.shift();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
});
}
return result;
}こちらも順を追っていきましょう。しかし、なんと深さ優先探索との違いは、データの取り出し方だけです。stackが配列をpop(最後尾を取り出し)して対して、今回はqueueを用意して(実質配列)shift(先頭から取り出し)していきます。※スタックとキューについてはこの記事が分かりやすいです。
AをforeachでループBとCを取り出す。
BとCは訪れていないのでフラグを立てる。→ここまで深さ優先探索一緒。
BとCの順にqueueにpush→ queue[B,C] result[A]
while分に入る。queueからBをshift→ここが違う → queue[C] result[A,B]
Bに紐づくA,Dを取り出す。Aは訪れたので、Dをキューにpushする(重要:DはCの後になる)→ queue[C,D] result[A,B]
Cをキューからshift() → queue[D] result[A,B]
次のadjacencyList[currentVertex]はCになる。Aは訪問済みなので、Eを取り出す。→ queue[D] result[A,B,C]
以後、繰り返し。
adjacencyList
{ A: [ 'B', 'C' ],
B: [ 'A', 'D' ],
C: [ 'A', 'E' ],
D: [ 'B', 'E', 'F' ],
E: [ 'C', 'D', 'F' ],
F: [ 'D', 'E' ] } }実行結果
>node graph.js
[ 'A', 'B', 'C', 'D', 'E', 'F' ]
深さ優先探索も、幅優先探索も途中までまったく同じアルゴリズムです。スタックとキュー、つまりデータ構造だけ違うのです。ノードを取り出す順序が違うのです。
結局、何が違うのでしょうか?
幅優先探索は「近い友達」の探索や、「最短距離を測るとき」に便利です。大量のデータがる場合の近い関係ですね。
深さ優先探索は、迷路を解く場合です。問題がそもそも解けるかどうかです。
プログラム最終版
class Graph {
constructor() {
this.adjacencyList = {};
}
//ノード追加
addVertex(vertex) {
this.adjacencyList[vertex] = [];
}
//無向グラフ
addEdge(v1, v2) {
this.adjacencyList[v1].push(v2);
this.adjacencyList[v2].push(v1);
}
//有向グラフ
addEdgeDirected(v1, v2) {
this.adjacencyList[v1].push(v2);
}
//エッジを削除
removeEdge(vertex1, vertex2) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
v => v !== vertex2
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
v => v !== vertex1
);
}
//ノードを削除
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
const adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex];
}
//深さ優先探索
depthFirstIterative(start) {
//ノードを格納するスタック
const stack = [start];
//訪れた順番を格納
const result = [];
//訪れたフラグ
const visited = {};
//現在のノード
let currentVertex;
//訪問済みフラグを立てる
visited[start] = true;
while (stack.length) {
currentVertex = stack.pop();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
});
}
return result;
}
//幅優先探索
breadthFirst(start) {
const queue = [start];
const result = [];
const visited = {};
let currentVertex;
visited[start] = true;
while (queue.length) {
currentVertex = queue.shift();
result.push(currentVertex);
this.adjacencyList[currentVertex].forEach(neighbor => {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
});
}
return result;
}
}いかがでしたか?ノードの中身に具体的な名前とかを入れて、現実世界の繋がりを表現して遊んでみてください。
ネットにいいサンプルがなかったので、自分で記事にしてみました。役に立つと感じたら、シェアしてくださいね!
日常の問題をアルゴリズムで解決していく良書。
