今回はスムージングの方法として、5 点移動平均法について説明します！

スムージング（平滑化）の話
１：概論
２：最小二乗法
３：5 点移動平均法 ← この記事！
４：グレヴィルの方法
５：まとめ

移動平均法のアイディア

移動平均法のアイディアについて説明しましょう。

まず、観測値は

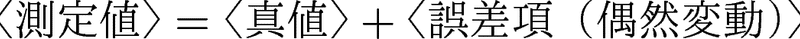
のように、真値に偶然変動の誤差項が混じったものと考えます。ここで誤差項は平均 0、分散 σ^2 の正規分布に従うと仮定しましょう。

このとき、誤差項の影響を小さくするには、どうすればいいでしょうか。

例えば次のような方法があります。i 番目の観測値、真値、誤差項をそれぞれ

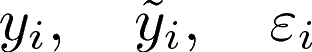
とおくと、これらの関係は

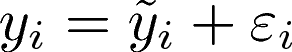
と表せます。ここで i 番目の周りの ( 2n + 1 ) 個の観測値の平均を考えます：

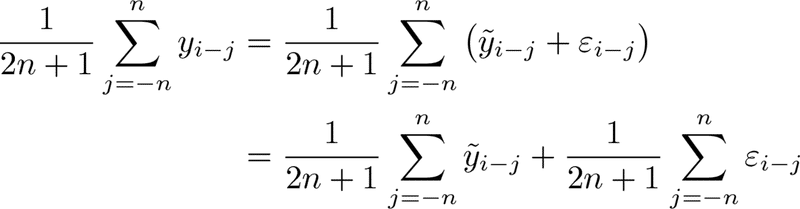
「真値が滑らかであること」を想定しているので、上式の最右辺第1項は、n が十分小さければ、おおよそ i 番目の真値となることが期待されます：

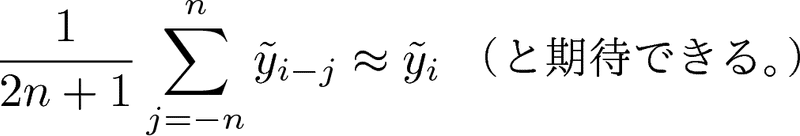
また、最右辺第2項については次のような考察ができます：

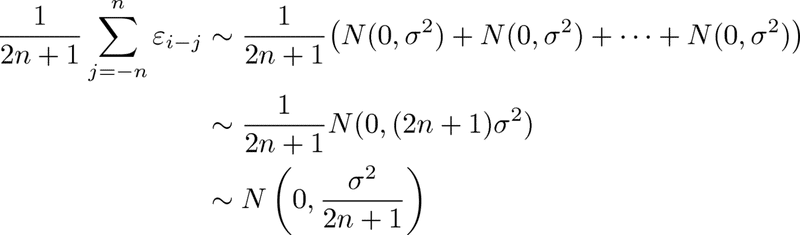
すなわち、分散が減少しており、誤差項の影響が小さくなっているといえます。

このように、測定値の ( 2n + 1 ) 点を平均することで、偶然変動の誤差項の影響を小さくする方法を ( 2n + 1 ) 点移動平均法と言います。

スムージング： 5 点移動平均法

ここからは具体的に 5 点移動平均法を実行してみましょう。

写真のように、ある測定値の周りの 5 点の平均を計算します。

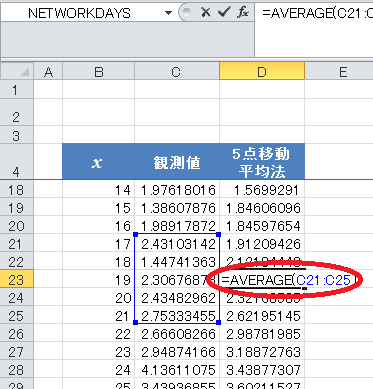
今回のスムージングの結果は下のようになりました！

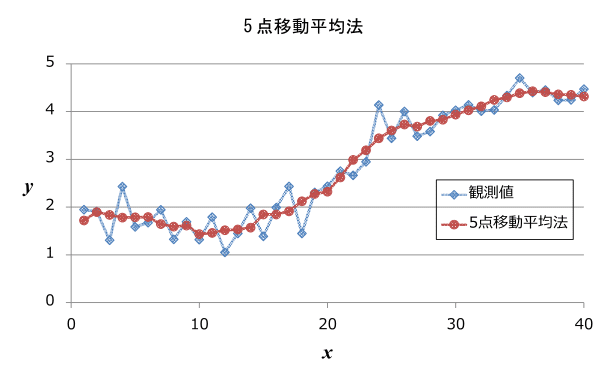
最小二乗法の直線よりも、「それっぽい」曲線となっていますね！

次回は移動平均法の 1 種であるグレヴィルの方法について説明します。

―――――
ありがとうございました！
ぜひ、スキ・フォローをお願いします！