ある集合の上に演算と同値関係が与えられていて、演算が同値関係と両立すると仮定しよう。前回『同値関係と両立する写像（２）』の命題２を、２つの写像としてその商集合への自然な全射の組（直積写像）と演算（Ｘの直積集合からＸへの写像）に対して適用する。

ここで、「演算が同値関係と両立する」とは、演算が同値類の選び方によらず一定の値を得ることをいう。

このとき、商集合上に、商集合への自然な全射が準同型となるような演算が引き起こされることをみよう。

なお、ここで演算は一般のｎ項演算でも通じるが、簡単のためよく使われる２項演算で考えよう。

１．演算が同値関係と両立する

集合Ｘに乗法と呼ばれる２項演算μ（または乗法の記号・で代用する）が定義されているとする：
　μ：Ｘ×Ｘ→Ｘ

そしてＸに同値関係～が与えられ、Ｘの同値関係～による商集合Ｘ／～をＸ’とする。この同値関係が演算μと両立すると仮定する。

ここで、演算μが同値関係～と両立するとは、
　ｘ～ｘ’　かつ　ｙ～ｙ’　⇒　ｘ・ｘ’～ｙ・ｙ’
　（ｘ，ｙ，ｘ’，ｙ’∈Ｘ）
であるときにいう。

２．商集合上に引き起こされる演算

写像π：Ｘ→Ｘ’を、Ｘの元ｘをその同値類[ｘ]へ対応させる自然な全射としよう：
　π(ｘ)＝[ｘ]
　　　＝｛ａ∈｜ａ～ｘ｝

「演算μが同値関係～と両立する」という仮定は、
　ｘ～ｘ’　かつ　ｙ～ｙ’　⇒　ｘ・ｘ’～ｙ・ｙ’
（ｘ，ｙ，ｘ’，ｙ’∈Ｘ）
即ち、
　π×π(ｘ，ｙ)＝π×π(ｘ’，ｙ’)　⇒　π◦μ(ｘ，ｙ)＝π◦μ(ｘ’，ｙ’)
（ｘ，ｙ，ｘ’，ｙ’∈Ｘ）
と書き換えられるから、
　「全射π×πの値で一致する２元は写像π◦μの値と一致する」
ことを意味する。

従って、命題２より写像
　ν：Ｘ’×Ｘ’→Ｘ’
　π◦μ＝ν◦(π×π)
となるものが一意的に存在する。

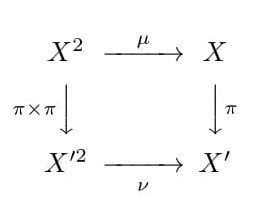
これは元で表示すると、ｘ，ｙ∈Ｘとするとき
　　　π◦μ(ｘ，ｙ)＝ν◦(π×π)(ｘ，ｙ)
　⇔　[ｘ・ｙ]＝ν([ｘ]，[ｙ])
である。

写像ν：Ｘ’×Ｘ’→Ｘ’はＸ’上の２項演算であり、それも乗法の記号（・）で書けば、上の等式は
　[ｘ]・[ｙ]＝[ｘ・ｙ]
と書かれる。

これが商集合上の乗法（・）の定義である。

そして同時にこの定義によって
　π(ｘ)・π(ｙ)＝π(ｘ・ｙ)
であるから、これは自然な全射π：Ｘ→Ｘ’が準同型写像であるということに他ならない。

３．まとめ

こうして自然な全射が準同型となるような商集合上の演算が、写像の構成原理によって自然に引き起こされることがわかる。（なお、証明していないがこの状況は一般のｎ項演算（ｎ≧０）でも成り立つ。そのときは２をｎで議論すればよい。）

一方、先に商集合の上の乗法を、
　[ｘ]・[ｙ]＝[ｘ・ｙ]　（ｘ，ｙ∈Ｘ）
で定義することから始まり、その定義がwell-definedであること、つまり代表元の取り方によらず矛盾なく定義されることを確認する、という話の進め方もよくある。この流儀では商集合の上にも乗法を定義したいという「気持ち」が先立つように感じる。

両者は商集合の視点からみれば、乗法が外部的に定義されるか、あるいは内部的に定義されるかという違いがある。