合同関係の全体と全射準同型の全体とが１：１対応し、合同関係全体における包含関係（順序関係）により全射準同型全体に順序を引き起こした。これらは束構造として互いに同型となり、それぞれを合同束、全射束と呼んだ。

束として同型だから下限は下限に、上限は上限に対応し合う。では、合同関係の上限、下限に対応する全射準同型の上限、下限は何だろうか。

今回は下限を構成する中で準直積（subdirect product）という概念が現れることをみよう。下限の特徴づけが準直積への全射準同型として得られる。

１．上限

代数系Ａを固定する。

Con(Ａ)をＡ上の合同束、Surj(Ａ)をＡ上の全射束とする。

ｆ，ｇ∈Surj(Ａ)とし、この2元の上限ｆ∨ｇを考えたい。

合同束に対応させると
　Ker(ｆ∨ｇ)＝Ker(ｆ)∨Ker(ｇ)
となる。

θ＝Ker(ｆ)，ψ＝Ker(ｇ)とおくと、
　θ∨ψ＝⋂ρ　
　（⋂はθ∪ψ⊂ρとなるρ∈Con(A)を動く）
である。

よって、
　ｆ∨ｇ＝⋀ｐ
　（⋀はｆ≦ｐ，ｇ≦ｐとなるｐ∈Surj(Ａ)を動く）
となり、このようなｐたちの「下限」である。

従って、一般に下限を求めることに帰着する。

２．下限

Ａを代数系として固定する。

Con(Ａ)をＡ上の合同関係全体、Surj(Ａ)をＡ上の全射準同型全体とおく。これらは集合ではないかもしれないからクラスとしておく。

θ，ψ∈Con(Ａ)、および対応してｆ，ｇ∈Surj(Ａ)を取ってくる：
　Ker(ｆ)＝θ，Ker(ｇ)＝ψ

Con(Ａ)における２元の下限は
　θ∩ψ
であったから、対応してSurj(Ａ)における２元の下限
　ｆ∧ｇ
がある。

ｆ∧ｇとしては
　ｆ∧ｇ：Ａ→Ａ／(θ∩ψ)
となる準同型写像である。

一方、
　ｋ：Ａ→(Ａ／θ)×(Ａ／ψ)
　　　ａ↦(ａ／θ，ａ／ψ)
を考えると、ｋの核は
　Ker(ｋ)＝θ∩ψ
である。

【証明】　
　　　(ｘ，ｙ)∈Ker(ｋ)
　⇔　ｋ(ｘ)＝ｋ(ｙ)
　⇔　(ｘ／θ，ｘ／ψ)＝(ｙ／θ，ｙ／ψ)
　⇔　ｘ／θ＝ｙ／θ，ｘ／ψ＝ｙ／ψ
　⇔　(ｘ，ｙ)∈θ，(ｘ，ｙ)∈ψ
　⇔　(ｘ，ｙ）∈θ∩ψ　■

従って「全射」に限るとしたら、このｋの行き先（終域）をｋの像：
　ｋ(Ａ)＝{(ａ／θ，ａ／ψ)｜ａ∈Ａ}
に限定すればよい。これをｋ’とおくと
　ｋ’：Ａ→ｋ(Ａ)，
　ｋ＝ｉ◦ｋ’，
　ただし、ｉ：ｋ(Ａ)⊂(Ａ／θ)×(Ａ／ψ)　（包含写像）
で、ｋ’は全射準同型でありその核は
　Ker(ｋ’)＝Ker(ｋ)
　　　　＝θ∩ψ
となる。

従って、
　ｋ’＝ｆ∧ｇ
を得る。

こうしてSurj(Ａ)における２元の下限を得ることができた。

３．性質

この考察から
　ｋ(Ａ)＝{(ａ／θ，ａ／ψ)｜ａ∈Ａ}
が満たす性質は明らかに、
（１）　ｉ：ｋ(Ａ)⊂(Ａ／θ)×(Ａ／ψ)　（包含写像）
そしてπ[θ]，π[ψ]をそれぞれ直積(Ａ／θ)×(Ａ／ψ)から成分への射影とすれば
（２）　π[θ]◦ｉ：ｋ(Ａ)→Ａ／θ，
　　　　π[ψ]◦ｉ：ｋ(Ａ)→Ａ／ψ
　　　はいずれも全射である
となる。

逆に、Ａ(１)，Ａ(２)がＡと同じような代数系で、Ａから同じような代数系Ｂへの全射準同型：
　φ：Ａ→Ｂ
が与えられ、
（１）　ｉ：Ｂ→Ａ(１)×Ａ(２)
　　　は単射準同型である
（２）　π[ｊ]◦ｉ：Ｂ→Ａ(ｊ)　（ｊ＝１，２）
　　　はいずれも全射である
を満たすならば、
　Ker(φ)＝Ker(ｆ)∩Ker(ｇ)
となる。

ただし、
　π[ｊ]：Ａ(１)×Ａ(２)→Ａ(ｊ)　（ｊ＝１，２）
は射影とし、
　ｆ：Ａ→Ａ(１)，ｇ：Ａ→Ａ(２)
は、合成：Ａ→Ｂ→Ａ(１)×Ａ(２)→Ａ(ｊ)
　ｆ＝π[１]◦ｉ◦φ，ｇ＝π[２]◦ｉ◦φ
とした。ここで条件（２）よりｆ，ｇは全射準同型である。

【証明】
　　　(ｘ，ｙ)∈Ker(φ)
　⇔　φ(ｘ)＝φ(ｙ)
　⇔　ｉ◦φ(ｘ)＝ｉ◦φ(ｙ)　　
　　（∵（⇐）は条件（１）より）
　⇔　π[ｊ](ｉ◦φ(ｘ))＝π[ｊ](ｉ◦φ(ｙ))　（ｊ＝１，２）
　　（∵（⇐）「直積」の定義より）
　⇔　ｆ(ｘ)＝ｆ(ｙ)，ｇ(ｘ)＝ｇ(ｙ)
　⇔　(ｘ，ｙ)∈Ker(ｆ)∩Ker(ｇ)　■

４．準直積の定義

全射準同型が２つ以上の場合でも、この議論と同様にすればよいだろう。そこで次のように定義しよう。

【定義（準直積）】
{Ａ(γ)；γ∈Γ}を同じような代数系の族とする。Ｂが族{Ａ(γ)；γ∈Γ}の準直積（subdirect product）であるとは、
（１）　ｉ：Ｂ→ΠＡ(γ)　
　　　は単射準同型である
（２）すべてのγ∈Γについて
　　　　π[γ]◦ｉ：Ｂ→Ａ(γ)
　　　が全射である
となるｉが存在するときにいう。ただし各γ∈Γで
　π[γ]：ΠＡ(γ)→Ａ(γ)，
　　　　(ｘ(γ)；γ∈Γ)↦ｘ(γ)
はＡ(γ)への射影（標準的な全射準同型）である。　

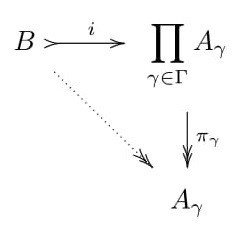
※すべてのγ∈Γで図式が可換

５．定理

任意個の直積についても成り立ち、定理として述べよう：

【定理（Birkhoff）】
Ａ，Ｂおよび族{Ａ(γ)；γ∈Γ}が全て同じ代数系とする。このとき、次は２条件は同値である：
（Ⅰ）全射準同型の族
　　　　{ｆ[γ]：Ａ→Ａ(γ)；γ∈Γ}
　　　が存在する。
（Ⅱ）全射準同型
　　　　φ：Ａ→Ｂ
　　　でＢが族{Ａ(γ)；γ∈Γ}の準直積である。

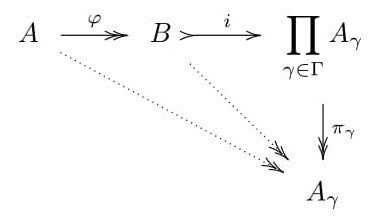
※すべてのγ∈Γで図式が可換

そしてこの同値な条件を満たすとき、（Ⅰ）の全射準同型族ｆ{[γ]}と（Ⅱ）の全射準同型φについて、
　Ker(φ)＝⋂Ker(ｆ[γ])　（⋂はγ∈Γを動く）
となる。

６．証明

２つの場合の証明と同様であるが、任意個の場合でも問題ないことを確認してみよう。

【証明】
（Ⅰ）⇒（Ⅱ）：
　　Ａ→ΠＡ(γ)
　　ａ↦(ａ(γ)；γ∈Γ)
　で定める準同型による像をＢとすれば、全射準同型
　　φ：Ａ→Ｂ
　　ａ↦(ａ(γ)；γ∈Γ)
　であって、Ｂは{Ａ(γ)；γ∈Γ}の準直積である。

（Ⅱ）⇒（Ⅰ）：
　各γ∈Γについて合成：
　　Ａ→Ｂ→ΠＡ(γ)→Ａ(γ)
　　ａ↦φ(ａ)↦ｉ◦φ(ａ)↦π[γ]◦ｉ◦φ(ａ)
　により
　　φ[γ]：Ａ→Ａ(γ)
　を定めれば、全射準同型である。
　（∵準直積の定義の（２）よりπ[γ]◦ｉ：Ｂ→Ａ(γ)の全射性）

後半については、
　ｆ[γ]＝π[γ]◦ｉ◦φ
より
　Ker(φ)⊂Ker(ｆ[γ])
が各γ∈Γでいえるから、
　Ker(φ)⊂⋂Ker(ｆ[γ])　（⋂はγ∈Γを動く）
である。また、
　　　(ｘ，ｙ)∈⋂Ker(ｆ[γ])　
　⇒　(ｘ，ｙ)∈⋂Ker(π[γ]◦ｉ◦φ)　
　⇒　すべてのγ∈Γについて、π[γ](ｉ◦φ(ｘ))＝π[γ](ｉ◦φ(ｙ))
　⇒　ｉ◦φ(ｘ)＝ｉ◦φ(ｙ)　　（∵直積の定義）
　⇒　φ(ｘ)＝φ(ｙ)　　　　　
　　　（∵準直積の定義の（１）によるｉの単射性）
　⇒　（ｘ，ｙ）∈Ker(φ)
より
　Ker(φ)⊃⋂Ker(ｆ[γ])
である。ゆえに両方合わせて、
　Ker(φ)＝⋂Ker(ｆ[γ])
である。■

７．まとめ

全射束の下限は、ある準直積への全射準同型ということで特徴づけられた。また全射束の上限も、それを含むすべての集まりの下限であり、よってある準直積への全射準同型であることがわかった。

８．補足事項

ざっとネット上で調べた限りではあるが”subdirect product”の日本語訳は今はまだないようだった。おそらくGarrett Birkhoffによる定義であると思われる。

Garrett Birkhoff：

また、本記事の「定理」については、Birkhoff氏の書籍を参考に編成した：
Garrett Birkhoff  ，Lattice Theory，American Mathematical Society Colloquium Publications Volume25，ChapterⅥ，§5