
【行間を読む】中原幹夫「理論物理学のための幾何学とトポロジー 第2版」p. 282 (Penroseのグラフ記法による共形変換でのRiemannテンソルの変換の導出 )
Penroseのグラフ記法について初見の場合はこちらから。
キーワード
共形変換 (Weyl変換)
Riemannテンソル
Penroseのグラフ記法
該当部分
$$
\begin{array}{rcl}\bar{R}(X,Y)Z&=&\cdots\\&=&\nabla_X\{\nabla_YZ+K(Y,Z)\}+K(X,\nabla_YZ+K(Y,Z))\\&&-\nabla_Y\{\nabla_XZ+K(X,Z)\}-K(Y,\nabla_XZ+K(X,Z))\\&&-\{\nabla_{[X,Y]}Z+K([X,Y],Z)\}\end{array}
$$
である。直接的だが少々退屈な計算の後
$$
\begin{array}{rcl}\bar{R}(X,Y)Z&=&R(X,Y)Z+\braket{\nabla_Xd\sigma, Z}Y-\braket{\nabla_Yd\sigma, Z}X\\&&-g(Y,Z)\nabla_XU+Y[\sigma]Z[\sigma]X\\&&-g(Y,Z)U[\sigma]X+X[\sigma]g(Y,Z)U\\&&+g(X,Z)\nabla_YU-X[\sigma]Z[\sigma]Y\\&&+g(X,Z)U[\sigma]Y-Y[\sigma]g(X,Z)U\end{array}
$$
が求まる。
解説
命題7.1より$${K(X,Y)=X[\sigma]Y+Y[\sigma]X-g(X,Y)U}$$である。$${U=g^{\mu\nu}∂_\mu\sigma e_\nu}$$なので
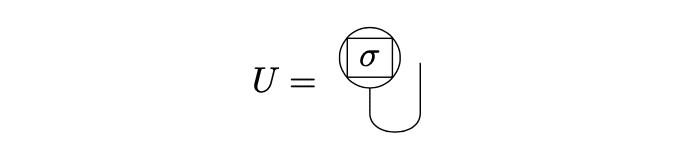
と描くことができ、
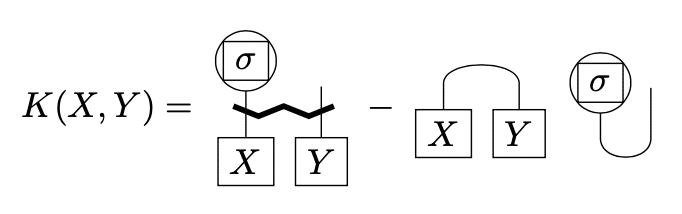
真っ直ぐな太線が反対称操作を表すことに対応。
である。(7.107)は
$$
\begin{array}{rcl}\bar{R}(X,Y)Z&=&R(X,Y)Z\\&=&\nabla_XK(Y,Z)+K(X,\nabla_YZ)+K(X,K(Y,Z))\\&&+(X\leftrightarrow Y)\\&&-K([X,Y],Z)\qquad\qquad(*)\end{array}
$$
書ける。右辺第2項は
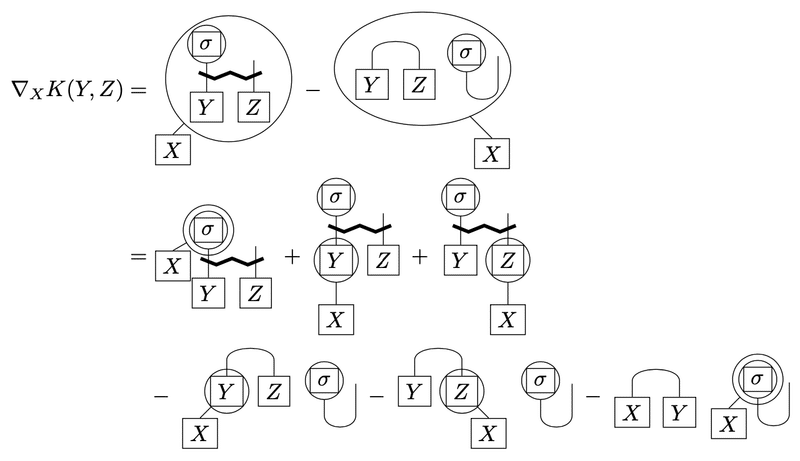
と式変形できる。(*)第3項、第4項、最終項はそれぞれ
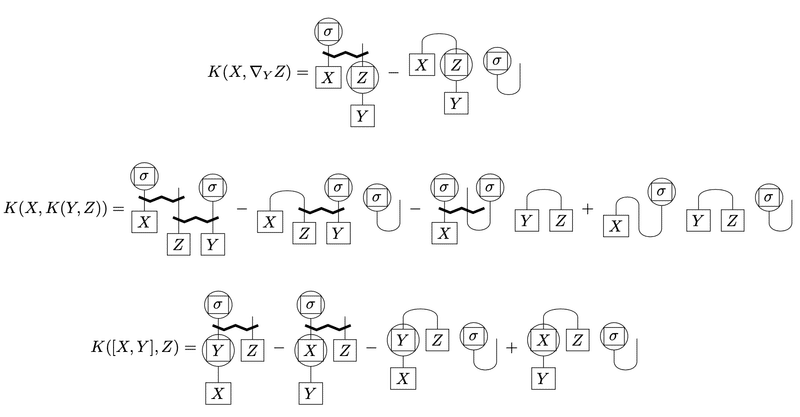
と描けるので、省略した$${X, Y}$$の入れ替えも併せて、全ての項を書き出すと下のようになる。

このうち、いくつかの項が消去され、

まとめたものの対称化演算子を適宜処理して図式を数式に解釈し直せば、
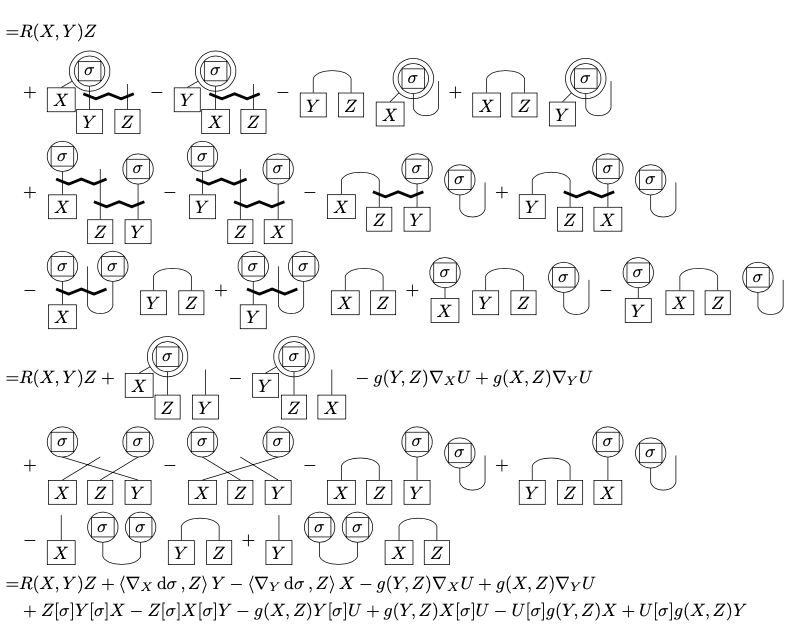
となって(7.108)を得る。
この記事が気に入ったらサポートをしてみませんか?
