キーワード

• 生成群

• 交換子

該当箇所

(ii) 3次元空間のベクトル$${\bm{V}}$$の成分を$${V_a\:(a=1,2,3)}$$のように書くと、aは、

$$
\hat{R}_a=-\sum_{b, c}\varepsilon_{abc}x_b\dfrac{∂}{∂x_c},\quad \hat{T}_a=-\dfrac{∂}{∂x_a}
$$

と書ける。少し計算することにより、次の交換子が得られる。すなわち、

$$
\begin{array}{l}\displaystyle[\hat{R}_a, \hat{R}_b]=\sum_{c=1}^3\varepsilon_{abc}\hat{R}_c,\\ \displaystyle[\hat{R}_a, \hat{T}_b]=\sum_{c=1}^3\varepsilon_{abc}\hat{T}_c,\\ [\hat{T}_a, \hat{T}_b]=0&\blacksquare\end{array}
$$

疑問点

「少し計算する」の計算過程。

解説

アインシュタインの縮約もさることながら、ペンローズのグラフ記法を使うと便利である。以下の2つを参照してから読まれたい。

$${\hat{R}_a}$$は次のように表される。

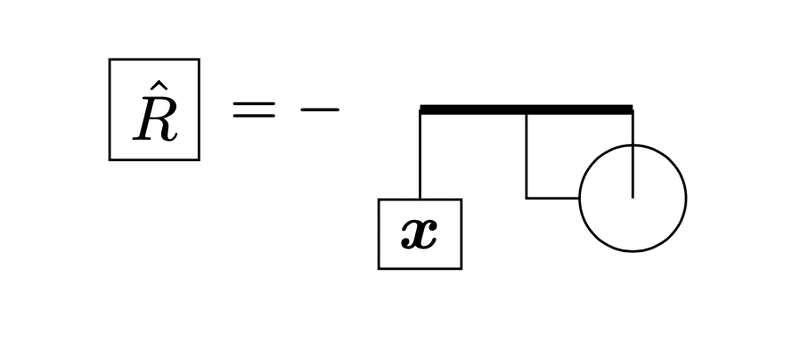
これを使って交換子$${[\hat{R}_a,\hat{R}_b]}$$を計算すると、下のようになる。ただし、一番右側の上が開いている棒が$${a}$$成分を、下が開いている棒が$${b}$$成分を表すものとする。

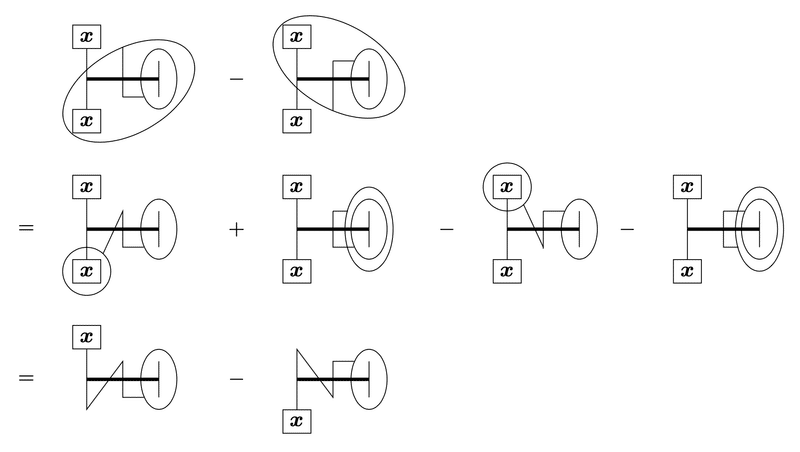
奇置換するとレビチビタの縮約ができる形になる。

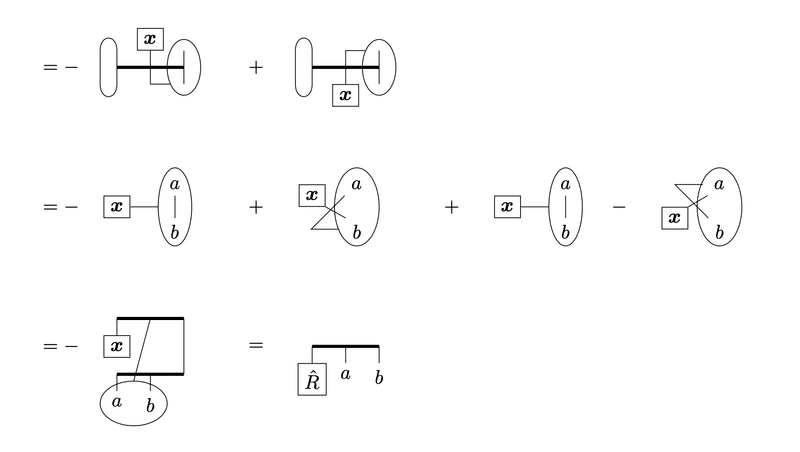
他については簡単に得られるので割愛。