ペンローズのグラフ記法による行列式と逆行列の表現
PDF版はこちらから。導出が豊富です。
誤植・質問はお気軽にコメントへお寄せください。
必要な知識
この記事では
学部教養課程の線形代数
レビチビタ記号
アインシュタインの縮約記法
についての知識を前提とします。また、「ペンローズのグラフ記法は初めましてです」という方は以下の記事でレビチビタ記号に関する部分を見ておくことをお勧めします。
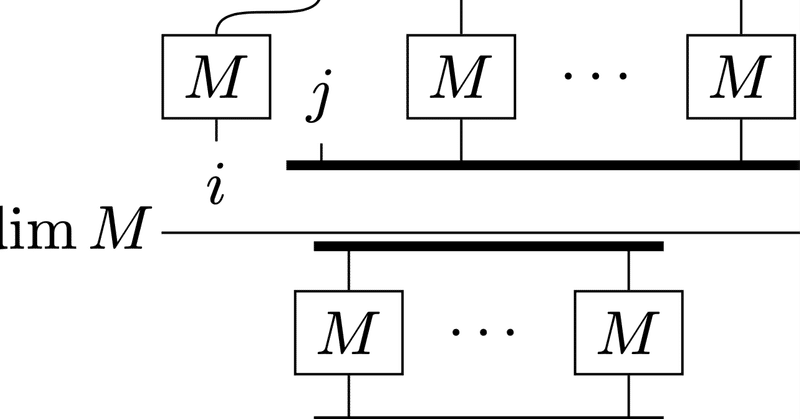
以下、行列$${M}$$の$${i}$$行$${j}$$列成分を$${M_i^j}$$で表します。また特別断りのない限り重複する添字は取りうる値を走らせて和を取ります。$${n=\dim M}$$です。
行列式の表現
行列式は定義によると
$$
\det M=\sum_{\sigma\in\mathfrak{S}_n}\mathrm{sgn}(\sigma)M_1^{\sigma_1}\cdots M_n^{\sigma_n}
$$
です。$${\mathfrak{S}_n}$$は$${n}$$次対称群です。
置換の符号はレビチビタ記号に一致することに注意してください。つまり、
$$
\det M=\epsilon_{\sigma_1\cdots\sigma_n}^{1\cdots n}M_1^{\sigma_1}\cdots M_n^{\sigma_n}
$$
と表せます。このままグラフ記法に落とし込むと行の添字の扱いが面倒なので、下付き添字についてもレビチビタ記号を経由して総和を取ります。
$$
\det M=\frac{1}{n!}\epsilon_{\sigma_1\cdots\sigma_n}^{1\cdots n}\epsilon^{\tau_1\cdots\tau_n}_{1\cdots n}M_{\tau_1}^{\sigma_1}\cdots M_{\tau_n}^{\sigma_n}
$$
右辺先頭の係数は$${\tau_k}$$の添字で生じる$${n!}$$通りの重複を解消しています。
ここまでを踏まえてグラフ記法を使い行列式を表すと以下のようになります。
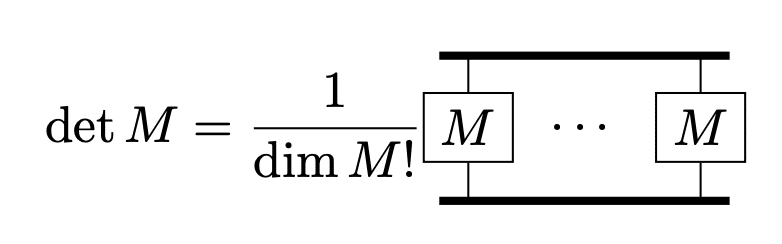
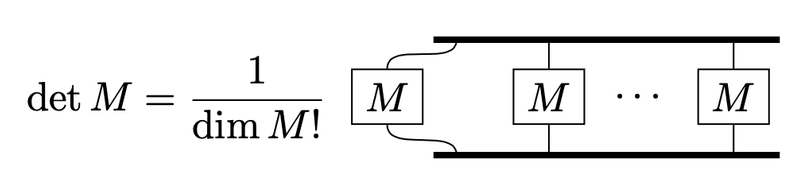
余因子展開
行列式は余因子展開によって表すことができます。先ほどのレビチビタ記号を使った行列式の表式を利用して、
$$
\det M=\frac{1}{\dim M}\sum_{i,j} (-1)^{i+j}M_i^j\frac{1}{(\dim M-1)!}\epsilon_{\sigma_1\cdots\sigma_{i-1}\sigma_{i+1}\cdots\sigma_n}^{1\cdots i-1,i+1\cdots n}\epsilon_{1\cdots j-1,j+1\cdots n}^{\tau_1\cdots\tau_{j-1}\tau_{j+1}\cdots\tau_n}M^{\sigma_1}_{\tau_1}\cdots M_{\tau_n}^{\sigma_n}
$$
です。$${\sigma_k, \tau_k}$$はそれぞれ$${\{1, \cdots, i-1, i+1, \cdots, n\}, \{1, \cdots, j-1, j+1, \cdots, n\}}$$を走るものとします。
符号$${(-1)^{i+j}}$$もレビチビタ記号に入れることができると簡単になります。
$$
\begin{array}{rl}\epsilon_{1\cdots i-1,i+1\cdots n}^{\sigma_1\cdots\sigma_{i-1}\sigma_{i+1}\cdots\sigma_n}\epsilon^{1\cdots j-1,j+1\cdots n}_{\tau_1\cdots\tau_{j-1}\tau_{j+1}\cdots\tau_n}&=\epsilon_{1\cdots i-1,i,i+1\cdots n}^{\sigma_1\cdots\sigma_{i-1},i,\sigma_{i+1}\cdots\sigma_n}\epsilon^{1\cdots j-1,j,j+1\cdots n}_{\tau_1\cdots\tau_{j-1},j,\tau_{j+1}\cdots\tau_n}\\&=\delta^i_{\sigma_i}\delta^{\tau_j}_j\epsilon_{1\cdots i-1,i,i+1\cdots n}^{\sigma_1\cdots\sigma_{i-1}\sigma_i\sigma_{i+1}\cdots\sigma_n}\epsilon^{1\cdots j-1,j,j+1\cdots n}_{\tau_1\cdots\tau_{j-1}\tau_j\tau_{j+1}\cdots\tau_n}\\&=(-1)^{i+j}\delta^i_{\sigma_i}\delta^{\tau_j}_j\epsilon_{1\cdots i-1,i,i+1\cdots n}^{\sigma_i\sigma_1\cdots\sigma_{i-1}\sigma_{i+1}\cdots\sigma_n}\epsilon^{1\cdots j-1,j,j+1\cdots n}_{\tau_j\tau_1\cdots\tau_{j-1}\tau_{j+1}\cdots\tau_n}\end{array}
$$
となることに注意して、
$$
\det M=\frac{1}{\dim M}M_{\sigma_i}^{\tau_j}\frac{1}{(\dim M-1)!}\epsilon_{1\cdots i-1,i,i+1\cdots n}^{\sigma_i\sigma_1\cdots\sigma_{i-1}\sigma_{i+1}\cdots\sigma_n}\epsilon^{1\cdots j-1,j,j+1\cdots n}_{\tau_j\tau_1\cdots\tau_{j-1}\tau_{j+1}\cdots\tau_n}M^{\sigma_1}_{\tau_1}\cdots M_{\tau_n}^{\sigma_n}
$$
です。
行列式の図式と比べると、$${M_{\sigma_i}^{\tau_j}}$$は先頭の記号$${M}$$に対応し、残りの$${\dim M-1}$$個が余因子とみなせます。係数$${1/(\dim M-1)!}$$は余因子の重複を解消し、$${1/\dim M}$$は先頭の$${M}$$の添字のうち片方について重複を解消しています。
もし片方の添字を回さないのであれば、先頭$${M}$$の足がきれて重複を解消する係数$${1/\dim M}$$が消えます。切れた足の添字は当然同じ。
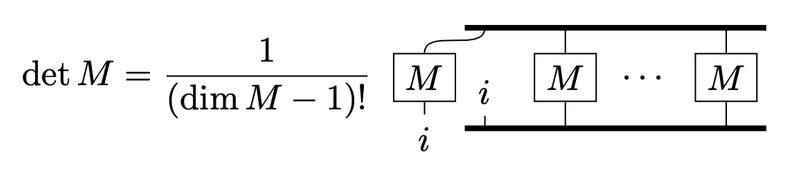
この状態は行列$${M}$$と余因子行列$${\tilde{M}}$$の行列積の$${ii}$$成分になっているはずですね。したがって余因子行列は次の形で書けることがわかります。
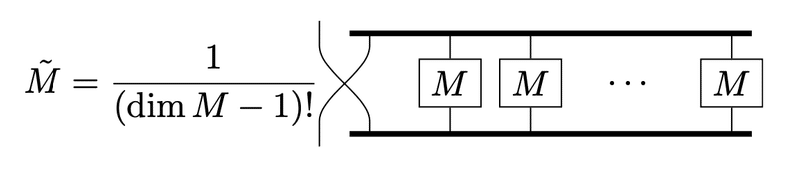
逆行列
余因子行列が描ければ逆行列もすぐに表すことができます。
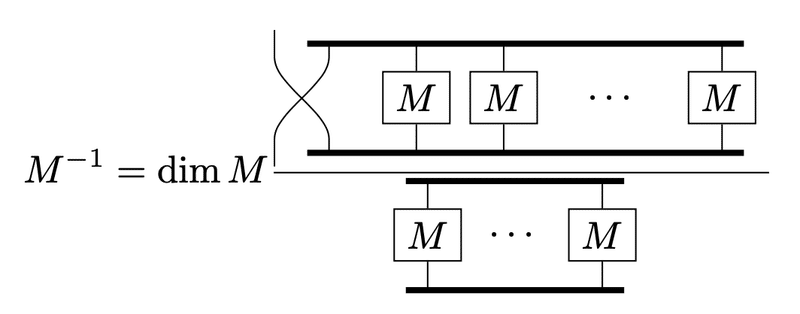
行列式の性質
定数倍の行列式
$$
\det(cA)=c^n\det A
$$
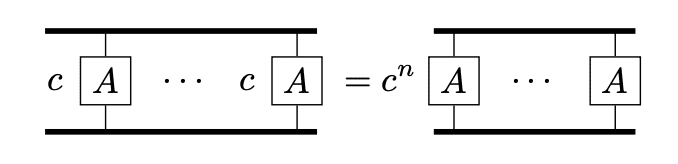
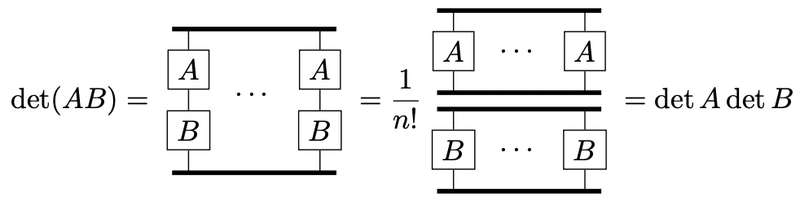
行列積の行列式
$$
\det AB=\det A\det B
$$
公式として
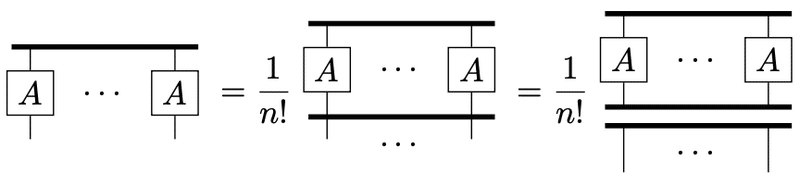
が成立する。したがって
転置の行列式
$$
\det A^T=\det A
$$
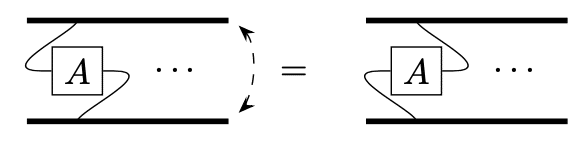
この記事が気に入ったらサポートをしてみませんか?
