こちらは私タイガーアイによるペンシルパズルアドベントカレンダー2018の19日目の記事になります。「のりのり」というニコリのパズルについてですが、ルールなどは省略するのでそちらは別途ニコリのHPなどをご覧ください。

先に1問載せましょう。以前、以下のようなのりのりを作成しました。

すぐ決まるところはないもののそこまでえげつなくもないので、まあ皆さんに仮定で解いていただいたのですが、いちおうこれにはテーマがありました。それが本記事のテーマでもある「のりの最密充填」です。

最密充填とは

ざっくり言えば、ある領域の中に何個まで黒マス("のり"ではない)を入れられるか、という発想です。ただし、ある領域とは必ずしも太線で区切られる"ブロック"とは一致せず、またのりが領域の内外にまたがることもあるとします。
先ほどの問題であれば、中央付近でいくつかのブロックをまとめると、7×7に近い領域(1マス出っ張っていますが)を作ることができます。このエリアを構成するブロックは13個なので、出っ張りを除いても7×7に少なくとも25個の黒マスが入る必要があります。後ほど詳しく触れますが、実はこれが最密充填になっており、そこから得られる情報を使えば先ほどの問題を解き進めることができるのです。

もし領域が無限に続いていれば、最密となるのりの詰め方は市松を片方向に2倍に引き伸ばしたような形になり、このときの充填率は50%になります。ところが、有限領域を考える場合はその限りではありません。以下では長方形(特に正方形)領域に対しての最密を考えていきます。

最密充填の具体形

2×2
これから充填を考えるにあたって、基本中の基本となるのが2×2の場合です。このとき黒マスは2マスまで入れることができ、以下の2パターンが考えられます(回転反転除く、以下も同様)。なお、左の場合は外部にのりがはみ出る必要がありますが、これ以降も含め領域外の黒マスは省略します。

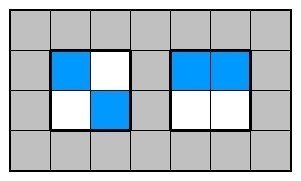
この充填率は50%です。そして、これが特に重要な点なのですが、2×2で分割できる領域に対しても最密充填率が50%であることがわかります。

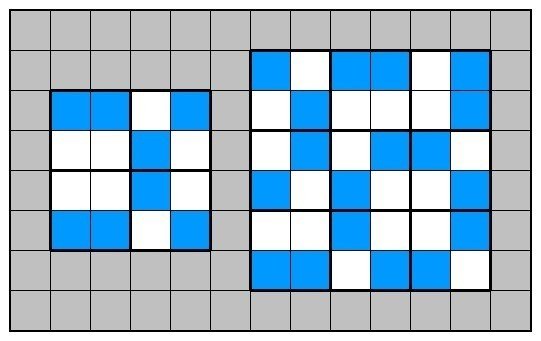
へやわけの部屋を分ける感覚に近いですが、この発想はこの先たびたび登場します。ただし、上の図からも察せられますが、少なくともそこまで大きくない領域に対してはどういう配置になるかはあまり決まらないようです。これについては後ほど触れることにします。

4×3
続いて4×3の長方形です。こちらは2×2での分割はできませんが、入る黒マスは最大6個になることが言えます。

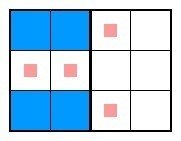
4×3に7個以上黒マスを入れようとすると、2×3に分割したとき片方には少なくとも4個入れる必要があります。そのためには上図のようにするしかありませんが、このとき右に3個入れることはできません。

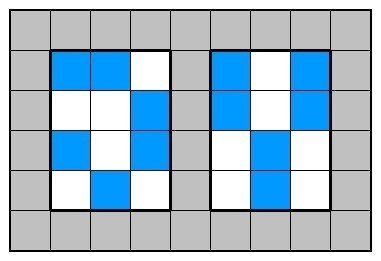
6個のパターンはまあだいぶあります。
さて、これを使うと4×n(n≧2)のとき最大充填率が50%であることがわかります。なぜなら、nが偶数なら2×2に分割できますし、奇数のnについては4×3から始めて4×2を繋げていけばよいからです。これも後でたくさん使っていきます。

(4m+2)×(2n+1)   (m≧0, n≧1)
4×n、2×2だけでは切りきれないこちらの場合ですが、このとき入る黒マスは最大(2m+1)(2n+1)+1個、すなわち充填率50%より黒マス1個だけ多く入れることができます。
まずm=0、すなわち2×奇数の場合ですが、2×2を詰めていくと端に2×1が残ります。ここをどちらも黒マスにすることで最密が実現され、芋づる式に黒マスの入り方が確定します。

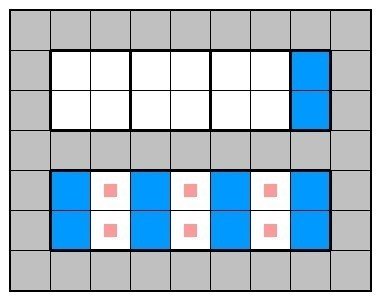
mが一般の場合も、幅4マスの長方形を作ることで2×奇数が現れます。切り方をずらしていくことで最密パターンが確定します。

3×3
さて、いよいよ奇数×奇数(特に正方形)のパターンを考えていきたいと思います。まずは3×3。5マスを黒にできるか考えていきます。

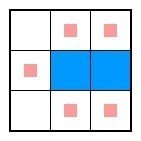
中央を黒マスにしてしまうと、それを含むのりが白マスを5個作ってしまうのでダメ。よって中央が白の場合を考えると、以下の2通りが考えられます。

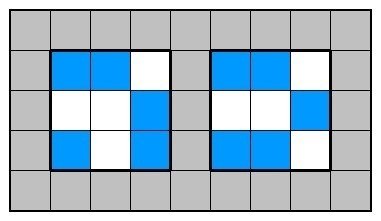
Tapaの122のパターンですね。したがって、3×3の最密充填は黒マス5個であり、さらにそのとき中央が白マスと確定することがわかります。最密を考えているのに白が決まるのはなかなか面白いですね。

5×5
次は5×5です。まず、14個入らないことは分かります。

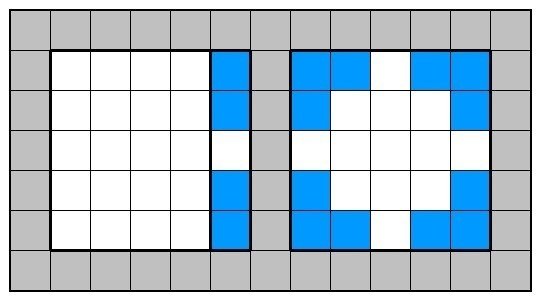
例えば5×4と5×1に分けたとき、5×4は最大10マス黒なので(4×n)、全部で14個の黒マスを入れるには1×5に4個入れる必要があります。そのためには左のようにするしかありませんが、切り方を変えると4辺すべてでこのようにしなければならないことがわかる(右図)ので破綻してしまいます。
では13個入るのかということですが、うまい方法が思いつかなかったので全探索してみました。その結果、13個のパターンは次の1通りのみでした。いいやり方があれば教えていただきたいです。

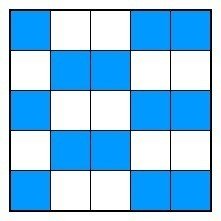
先ほども少し出ましたが、市松的パターンを切り出したような形です。

少し考えると、奇数×奇数の場合にはこの市松的パターンが有効であることがわかります(4で割った余りが1か3かによって少し異なりますが)。これを使えばマス数Sの奇数×奇数領域には少なくとも(S+1)/2個の黒マスを入れることができます。

7×7
どんどん大きくしていきましょう。7×7です。これ以降は、マス数Sに対して最密が黒マス(S+1)/2であることが容易にわかるので、この場合の黒マス配置のパターンがいくつあるか、ということに絞って考えていきたいと思います。
7×7になると、うまく領域を分割してやることで確定するマスがあります。

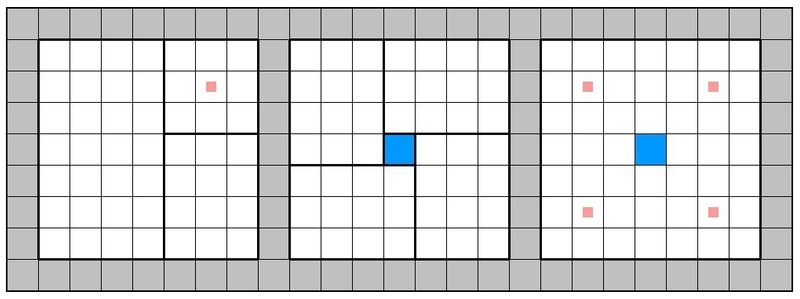
まず4×7、4×3を入れることで端に3×3を作ることができます。最密時に3×3の中央は白くなることを思い出すと、四隅から1つ内側にずれたマスが白くなることがわかります。一方、4×3を4個作ってやると中央に1マスだけ残るので、ここが黒マスであることも確定します。
分割法によって確定するマスは多分ここまでです。なお、最初の問題はこれを考えると論理的に解くことができます。
さて、4×3が4個の分割をベースに、より詳しくパターンを詰めていきましょう。

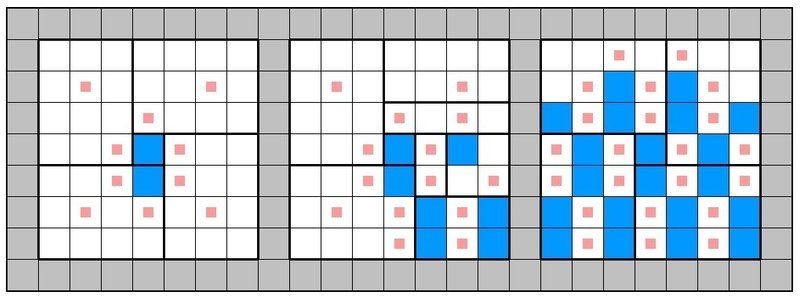
まず、中央の黒マスを含むのりを作ります。方向はどちらでもよいのでとりあえず下に伸ばします。すると、上図中央のように右下の4×3を1×2、2×2、2×3と分けてやると、それぞれに入る黒マスがそれぞれ0、2、4に確定します。
2×3は配置も確定しますが、2×2の入れ方は2通りあります。ここでさらに右上領域を4×2と4×1に分けてやれば、4×1に2個入れるために1通りに定まります。同時に上側も結構決まりますね。
ここまでの議論は4×3の分割法を変えても成立するはずです。よって、上図右のように領域の左側についても同様に決めることができます。

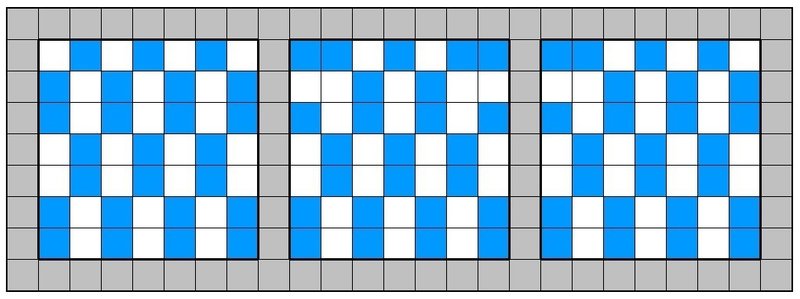
さてこのまま全体の配置が決定する…かと思ったら、しません。左右の上側の隅で2パターンの配置が可能で、全部で3通りが考えられます。ただし本質はだいたい同じで、やはり市松型が強いことがわかりました。また、これらを回転反転させつつ確定マスを探すと、先程決まった5マス以外に確定マスはないことが確かめられます。

9×9
9×9の場合、タテとヨコからそれぞれ4マスずつ切り取ってやれば5×5の最密充填が現れます。したがって7×7のときに3×3を作ったときと同様、4隅に5×5ができるのですが、9×9からはこいつらが重なるようになります。5×5の最密充填は配置まで確定することを考えてダブった部分を手掛かりにすると、9×9の最密はこれまた以下のような市松模様ただ1通りであることが判明します。

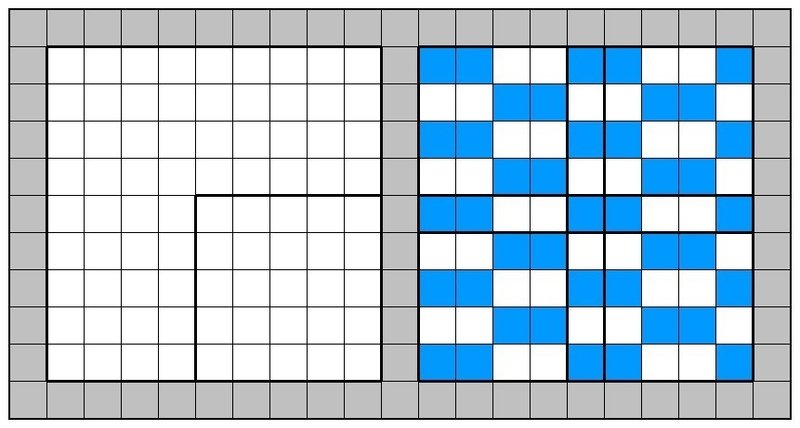
一般の一辺が奇数の正方形
上記の考え方は一般の一辺が奇数の正方形に対しても帰納的に適用できます。つまり、n≧1について

一辺が4n+1の正方形の場合、最密充填解は市松型1通りのみ
一辺が4n+3の正方形の場合、最密充填解は市松型をベースに角のうち2箇所で2択となり合計3通り

が言えます。

2n×2nの最密充填解の個数

さて、2n×2nの場合は2×2に分割できるため最密充填率は50%であったわけですが、小さいnについてはそれなりに多様なパターンがあるようでした。しかし、nが大きくなってくるとこちらも市松をベースにせざるを得ない気がします。ということで具体的に何個最密充填解があるのか調べてみました。
4×4の場合はこちら。

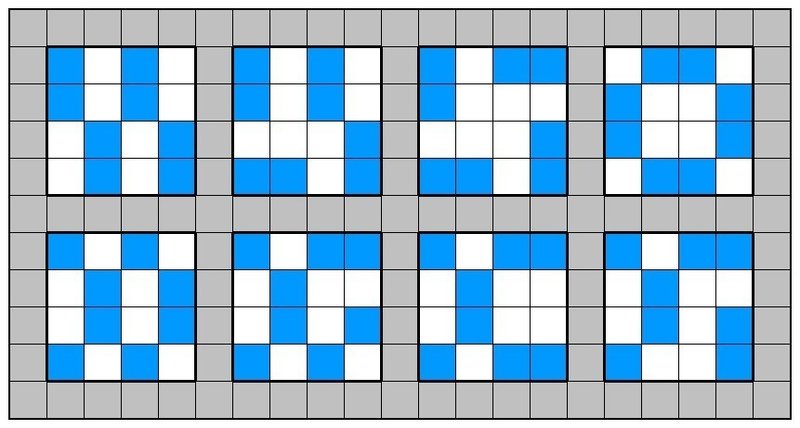
上記の8通り。けっこうバラバラです。続いて6×6。

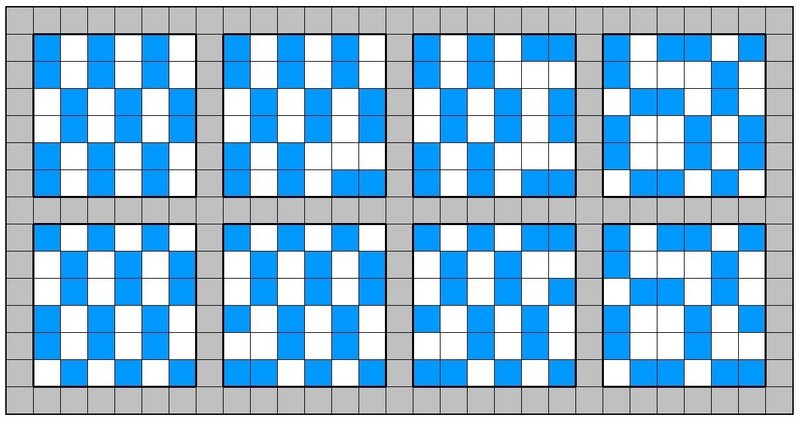
なんとなく規則性が見えてきました。右2つが小サイズ特有解という感じがします。さらに8×8。

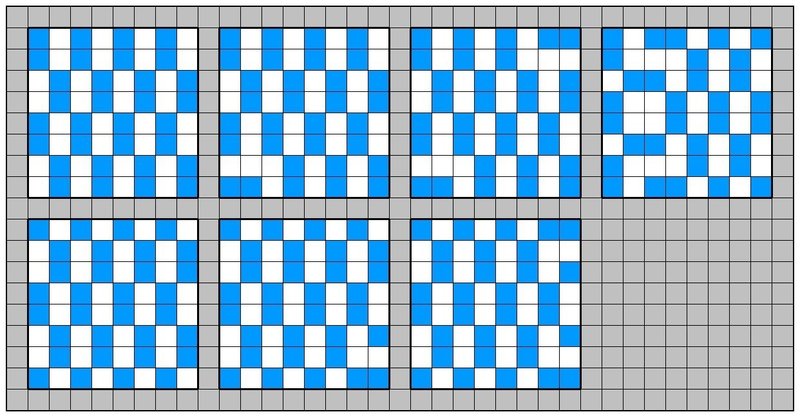
解は7個。右上以外は市松模様をベースに角を変えたものです。

10×10以上もやってみましたが、これ以上は解は6個、つまり上の図でいう左3列のパターンでした。というわけで、2n×2nについてはnが4以下の場合に限り小サイズ特有の詰め方があるようです。

今回触れきれなかったこと

5×7のような正方形でない奇数×奇数の長方形についても、「面積Sに対して(S+1)/2個まで黒マスを入れられる」が言えます。3×5に8個入ることがわかるので、3×3、3×5、5×5のいずれかから出発して4×nをくっつけてやれば説明できます。ただ、この場合どのようなパターンがあるかまでは考えていません。
のりの形を変えてやるのも面白そうです。1×nの場合ならまだしも、Lトリオミノとかになるとカオスが見れそう…。

おわりに

あまりまとまっていないため少し読みづらかったかもしれません。ごめんなさい…。また、ミスなどあればご指摘いただけると幸いです。
私はいわゆる大規模手筋が好きなので、のりのりという局所手筋が基本のパズルにあって盤面全体を見渡せるこの最密充填はお気に入りです。ただし、これを成立させるには(奇数×奇数だと)3マスのブロックが必須ということもあって仮定に弱いという欠点がありますが…。みなさんも、もしブロックが詰まっているのりのりを見かけたら(仮定する前に)これを思い出していただければ、もしかすると活用できるかもしれません。