abstract　手元のデータには含まれていない新規のカテゴリが出現する確率を推定する課題は、機械学習でしばしば登場する問題です。このnoteでは、代表的なアプローチの一つであるGood-Turing推定量を簡単に紹介します。

1　Introduction

機械学習課題では、まだ見ぬカテゴリが今後どれくらい出現する可能性があるのか、その確率を推定したいことがあります。例えば、装置の異常パターンを類別するような課題です。未知の異常パターンが出現する確率を推定することで、現状の類別がどれくらい十分なのかを検討することができます。

この問題を次のように定式化してみましょう。

そんなこと本当にできるのか？と思う方も多いのではないでしょうか。今回は、この確率 $${p}$$ の値の推定量として知られるGood-Turing推定量を紹介します。

2　Good-Turing推定量

標本 $${x=\{x_1,\cdots,x_n\}}$$ に1回だけ出現したカテゴリの数を $${|S_1|}$$ と表すことにします。このとき、確率 $${p}$$ を

$$
\begin{align*}
\hat{p} &= \frac{|S_1|}{n}
\end{align*}
$$

と推定することにしましょう。これをGood-Turing推定量といいます。この推定量の適切さを議論することは難しいですが、第3節で簡単に説明を与えます。

ここではGood-Turing推定量を具体例で計算し、まずは慣れることにしましょう。以下のような例題を考えます。

今回、1回だけ出現したカテゴリの数は $${|S_1|=3}$$ です。標本のサイズは $${n=100}$$ なので、次の測定で現在わかっている10種類以外の異常パターンが確認される確率 $${p}$$ の値は $${\hat{p}=3/100}$$ と推定できます。

3　なぜこの定義式で良いのか？

Good-Turing推定量の定義式を直感的に納得するのは難しいでしょう。そこで今回は、この定義式の妥当性をR言語を用いた数値実験・数理統計的な議論の二通りで考えます。

3.1　R言語を用いた数値実験

次のような設定で数値実験を実施します。カテゴリの出現確率の分布は $${s=1}$$ のZipf分布として知られているものです。
(1)　カテゴリ数 $${K=100}$$
(2)　各カテゴリの確率 $${p_k=\displaystyle\frac{1/k}{\displaystyle\sum_{j=1}^{K}1/j}}$$, $${k=1,\cdots,K}$$
(3)　標本サイズ $${n = 100, 200, \cdots, 2500}$$

ここでは二種類の結果を示します。一つは標本サイズが $${n=100}$$ の場合に、確率 $${p}$$ の値とGood-Turing推定量の値 $${\hat{p}}$$ を比較する散布図を示します。もう一つは、標本サイズ $${n}$$ に対して誤差 $${\hat{p}-p}$$ の大きさがどのように変化するのかを示します。

以下、指定したカテゴリ数と標本サイズの設定のもとで、確率 $${p}$$ の値とGood-Turing推定量の値 $${\hat{p}}$$ を計算する関数を示します。

# 確率pとGood-Turing推定量p_hatの計算
gt_estimate <- function (K, n, n_iter) {
    # K: int, カテゴリ数
    # n: int, 標本サイズ
    # n_iter: int, 数値実験の繰り返しの回数
    
    # 計算結果を記録するためのオブジェクト
    p <- c()    # 次の測定で標本xに含まれないカテゴリが出現する確率
    p_hat <- c()    # Good-Turing推定量

    # Zipf分布の確率をカテゴリに割り当てる
    prob_unnormed <- 1/(1:K)    #　逆数に比例する確率を割り当てる
    prob <- prob_unnormed/sum(prob_unnormed)    # 確率の総和を1にする
    
    # 数値実験をn_iter回繰り返す
    for (i in 1:n_iter) {
        x <- sample(1:K, size = n, prob = prob, replace = TRUE)    # 標本抽出
        tab <- table(x)    # 出現したカテゴリとその出現数を示すテーブル
        S0c <- as.numeric(names(tab))    # 出現したカテゴリ名をテーブルから抽出する
        p[i] <- 1 - sum(prob[S0c])    # 次の測定で標本xに含まれないカテゴリが出現する確率
        S1 <- tab[which(tab == 1)]    # 標本xに一回だけ出現したカテゴリを取得する
        p_hat[i] <- length(S1)/n    # Good-Turing推定量
    }
    
    # 結果をデータフレームにまとめる
    result <- data.frame(p, p_hat)
    return(result)
}

3.2　確率の値とGood-Turing推定量の値の比較

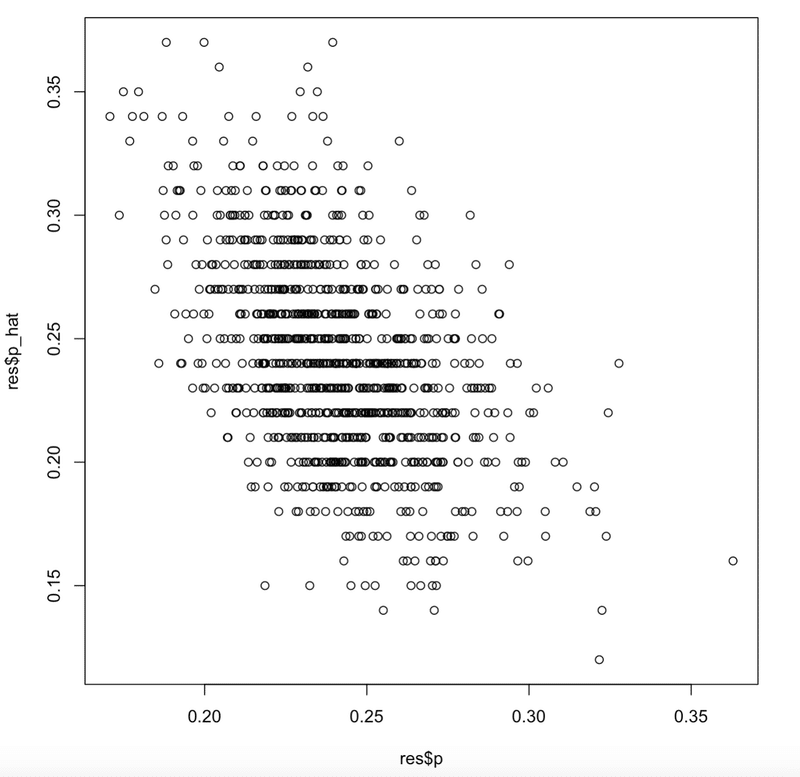
カテゴリ数 $${K=100}$$、標本サイズ $${n=100}$$ の設定のもとで、数値実験を1000回繰り返し、各実験における確率 $${p}$$ の値とそのGood-Turing推定量の値 $${\hat{p}}$$ の値を比較した散布図を示します。

# 確率の値とGood-Turing推定量の値の比較
res <- gt_estimate(K = 100, n = 100, n_iter = 1000)
plot(res$p, res$p_hat)

この結果、以下のFig 1に掲げる散布図が得られます。確率 $${p}$$ の平均値とGood-Turing推定量 $${\hat{p}}$$ の平均値がほぼ等しいことを確認できます。3.4節では、これが一般論であることを数理統計的な議論で示します。

3.3　標本サイズに対する誤差の大きさの変化

3.2節では誤差 $${\hat{p}-p}$$ の大きさについては議論しませんでした。ここでは、標本サイズ $${n}$$ に対して誤差の大きさがどのように変化するのかを議論します。

# 標本サイズに対する誤差の大きさの変化
n_candidate <- seq(from = 100, to = 2500, by = 100)    # 数値実験する標本サイズ

error <- c()    # 誤差を記録するオブジェクト
for (n in n_candidate) {
    res <- gt_estimate(K = 100, n = n, n_iter = 1000)    # 数値実験
    error <- c(error, res$p_hat-res$p)    # 結果の記録
}

size <- rep(n_exp, each = 1000)    # グラフの横軸
plot(size, error)

この結果、以下の散布図Fig 2が得られます。この図から誤差の大きさは、標本サイズ $${n}$$ が大きくなるにつれて0に近い値を取りやすくなることがわかります。この事実もまた一般的に成り立ちます。詳細を知りたい方は、論文[MS]のTheorem 3などを参考にされてください。

3.4　数理統計的な議論

3.2節で確認した「確率 $${p}$$ の平均値とGood-Turing推定量 $${\hat{p}}$$ の平均値がほぼ等しい」という現象が一般に成り立つことを証明します。具体的には以下の定理が成り立ちます。

定理　次に測定される標本点 $${x_{n+1}}$$ のカテゴリが、すでに得られたサイズ $${n}$$ の標本 $${x=\{x_1,\cdots,x_n\}}$$ に一つだけしか含まれないようなカテゴリである確率を $${p_1}$$ と表すことにします。このとき、以下が成り立ちます。

$$
\begin{align*}
\mathbb{E}[p] &= \mathbb{E}[\hat{p}] - \frac{1}{n}\mathbb{E}[p_1]
\end{align*}
$$

この定理は、標本のサイズ $${n}$$ が十分に大きければ、確率 $${p}$$ の期待値とGood-Turing推定量 $${\hat{p}}$$ の期待値が一致する（つまりバイアスがない）ことを意味しています。

証明　$${S_k}$$ を標本 $${x=\{x_1,\cdots,x_n\}}$$ に $${k}$$ 回だけ出現するようなカテゴリ全体の集合だとします。今回重要なのは $${S_0,S_1}$$ です。左辺の期待値 $${\mathbb{E}[p]}$$ は集合 $${S_0}$$ を用いて、以下のように表すことができます。

$$
\begin{align*}
\mathbb{E}[p] &= \sum_{k=1}^{K}p_k\mathbb{P}[C_k\in S_0]
\end{align*}
$$

カテゴリ $${C_k}$$ が集合 $${S_0}$$ に属する確率は $${\mathbb{P}[C_k\in S_0]=(1-p_k)^n}$$ です。また、カテゴリ $${C_k}$$ が集合 $${S_1}$$ に属する確率は $${\mathbb{P}[C_k\in S_1]=np_k{(1-p_k)^{n-1}}}$$ です。これを用いると、以下のような式変形ができます。

$$
\begin{align*}
\mathbb{E}[p] &= \sum_{k=1}^{K}p_k(1-p_k)^n\\
&= \frac{1}{n}\sum_{k=1}^{K}np_k(1-p_{k-1})^{n-1} -  \frac{1}{n}\sum_{k=1}^{K}\left(p_k\times np_k(1-p_{k-1})^{n-1}\right)\\
&= \frac{1}{n}\sum_{k=1}^{K}\mathbb{P}[C_k\in S_1] - \frac{1}{n}\sum_{k=1}^{K}p_k\mathbb{P}[C_k\in S_1]\\
&= \frac{1}{n}\mathbb{E}[|S_1|] - \frac{1}{n}\mathbb{E}[p_1]\\
&= \mathbb{E}[\hat{p}] - \frac{1}{n}\mathbb{E}[p_1]
\end{align*}
$$

以上で定理が証明できました。■

Acknowledgement

このnoteはすうがくぶんか Advent Calendar 2023の15日めの記事として書いたものです。日頃から統計学と関わる機会を下さっている受講生の皆さまに感謝申し上げます。

References

[G]　Good, I. J. (1953). The population frequencies of species and the estimation of population parameters. Biometrika, 40(3-4), 237-264.
[MS]　McAllester, D. A., & Schapire, R. E. (2000, June). On the Convergence Rate of Good-Turing Estimators. In COLT (pp. 1-6).