小学生の娘とキャッチボールをしました。子どもとキャッチボールするというのは、私の夢の1つだったので、幸せを感じながら、楽しめました。

娘はソフトボールもほとんどやっていないというので、近い距離でゆっくり投げていました。娘が暴投しても、ジャンプしたり、少し走ったりして、私にはいい運動になりました。若いつもりで、思いっきりジャンプして、腰を痛めそうになりましたが……。

私は、娘がとりやすいように、できるだけスピードはおさえて、胸のあたりに届くように意識していました。しかし、久しぶりで距離感がつかめず、ワンバウンドや、娘の頭の上に投げてしまうことも多々ありました。特に、フライの練習がてら、高く投げると目測をあやまって、やはり頭の上を通過しがちでした。

ある程度、速く投げるとコントロールしやすいですが、スピードをおさえると逆に狙いにくいです。

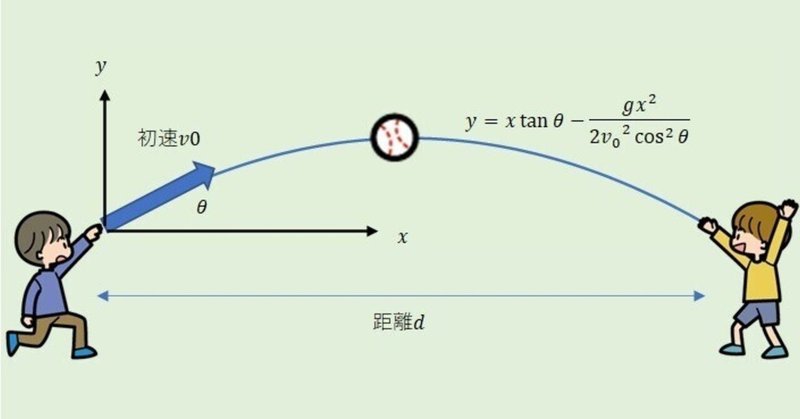
そんなことを、すっきり確認したくなり、少し計算してみました。（数式に抵抗がある方は、この後の数行は軽く流していただいて、かまいません。）

簡単のため、風や空気抵抗は無視すると、投げたボールの軌道は放物線（2次関数のグラフ）になります。初速$${v_0}$$、投げる角度$${\theta}$$、相手までの距離$${d}$$、重力加速度$${g}$$とすると、相手にストライクで届く条件は

$$
v_0 = \sqrt {\frac{gd}{\sin 2 \theta}}
$$

となります。式だとピンとこないと思いますので、グラフにしてみました。

経験的にはわかりますが、次のことを確認できます。

•   距離が離れるにつれ、一定以上の初速度で投げないと、相手に届かない。

• 角度45°でもっとも遠くへ投げられる。（角度45°付近だと初速度は遅くする必要あり。）

• 初速度を決めると、相手の胸元に投げ込むには、低角度（通常）と高角度（フライ）の2種類の方法がある。

身の回りの現象を物理や数学で表現できるというのが、伝えたいことです。2次関数や三角関数なんて役に立たないと思われるかもしれませんが、少しだけ身近に感じてもらえれば、うれしいです。

そうは言っても、キャッチボールは、あれこれ計算するよりも、やりながら感覚を身につける（取り戻す）方が重要なのでしょうね。とりやすいボールを投げて、子どもが「またやりたい」と言ってくれるよう、がんばります。