講義ウェブサイトはこちらです。
第6回講義＜前編＞はこちらです。
-------------------------------------

第6回目の後半では，前半で学んだvNM効用関数を活用して，リスクに対する態度と，ゼックハウザーのパラドックスと呼ばれる面白い（？）問題について解説しました。

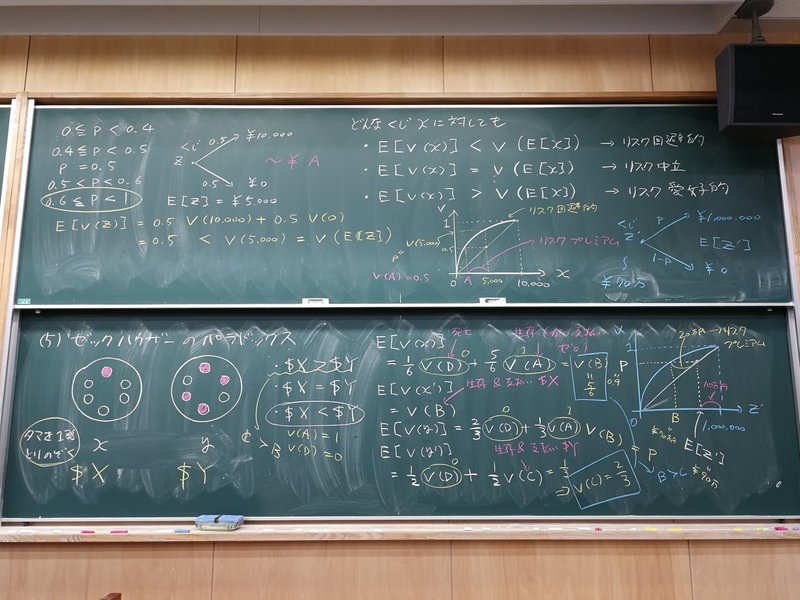
【板書】　vNM効用関数とリスクに対する態度の関係。不確実なくじxに対する（事前の）期待効用と，期待金額を確実に受け取る場合の（vで測った）効用の大小関係から，以下が定義される。
・期待効用 < 期待金額の効用 ⇔ リスク回避的（risk averse）
・期待効用 = 期待金額の効用 ⇔ リスク中立（risk neutral）
・期待効用 > 期待金額の効用 ⇔ リスク愛好的（risk loving）

保険契約の問題などを分析するときは，リスク回避が仮定されます。上の定義から，どんなくじxに対しても
・v(E[x]) > E[v(x)] 
となりますが，ここでくじxと無差別になるような確定的な結果，つまり
・E[v(x)] = v(A)
となるようなAを求めることができます。このAを確実性等価（certainty equivalent）と呼びます。さて，上の二つの式から
・v(E[x]) > v(A) ⇔ E[x] > A
となるため，くじxの期待金額E[x]は，確実性等価Aよりも大きいことが分かります。この差額をリスクプレミアムと呼びます。数式で表すと，
・リスクプレミアム = E[x] - A >0
となります。これは，リスク回避的な人がくじxに関する
・リスクを解消するためにいくらまで支払う意欲があるか
を表現していると解釈できます。

ゼックハウザーのパラドックスは，ロシアンルーレット（弾が最大で6発装填できる銃を想定）に関するちょっと変わったパラドックスです。今あなたが，一度だけ銃口を自分の頭に当てて銃の引き金を引かなければいけない状況を想定してください。以下のxとy二つのシナリオで，もしも「お金を支払うことで弾を一つだけ取り除くことができる」とすると，最大限支払ってもよい金額を比較したときに，どちらの方がよりたくさん払いたいと思いますか？
・x：もともと弾が1発だけ込められている（死亡確率=1/6）
・y：もともと弾が4発込められている（死亡確率=4/6=2/3）

教室では，大多数の学生がxで弾を取り除くための支払い意欲$Xの方が，yにおける支払い意欲$Yよりも大きい，と答えました。しかし，期待効用理論にもとづくと答えはその逆，つまり
・リスクに対する態度がどんなものであっても，$Y>$X
となることが示されます。（ただし，生き残った場合の効用は所持金の影響を受ける一方で，運悪く自分が死んだ場合の効用は死ぬ直前の所持金には一切依存しない，という強い仮定を置いています）

なぜそうなるのか，黒板の計算式をヒントに考えてみてください！ちなみに，板書のA~Dは以下の状態を表しています。
・A：一銭も払わずに生存 → 最善の結果（v(A)=1と標準化）
・B：$X支払って生存
・C：$Y支払って生存
・D：死亡 → 最悪の結果（v(D)=0と標準化）
また，x'とy'は以下の状況を表しています。
・x'：xから$X払って弾を一つ取り除いた状況（死亡確率=0）
・y'：yから$Y払って弾を一つ取り除いた状況（死亡確率=3/6=1/2）
あとは，xとx'が無差別，yとy'が無差別である，という（支払い意欲の定義から無差別になる点に注意）想定から，期待効用をそれぞれ計算すれば結果が求まります。（v(B)=5/6, v(C)=2/3から，$X<$Yが導かれます。）