こちらで着手した「はてなブログ時代の投稿の見直し作業」が想定通り難航しています。事前に用意した仮説が次々と破綻したりして、まさしく「仁義なき色即是空空即是色」状態に突入…

その作業の最中、私自身が念仏の様に繰り返し唱え続けているのが以下の数理となります。いやはや今回は本当にそれくらいしかお出し出来るものが…

原始的デカルト直交座標系イメージからの脱出

小学校の頃から、時空間座標系をなんとなく大雑把に以下の様にイメージしてきました。「連続する点(0次元)を束ねれば線(1次元)になり、連続する線を束ねれば面(2次元)となり、連続する面を束ねれば立体(3次元)となり、さらに時間はこの考え方の枠組みを超越する形で実在する」。実は文面自体に間違いはなく、その在り方についての私自身のイメージ力が追いついてなかっただけとも。以前にも指摘しましたが、まさにこれこそが「カンブリア爆発期に生物が授かった視覚と視覚情報を処理する脊髄に由来する思考的限界」という次第。フロイトの名言「なるほど確かに自由は人間を解放する。ただし自由にではない」というやつそれでは今はどういう考え方を採用しているかというと…

数値2個からの再出発

(同一数直線上の)「実数値」が２個あれば、その相加平均$${\bar{a_0b_0}＝\frac{a_0+b_0}{2}}$$から偏差$${a_1=a_0-\bar{a_0b_0},b_1=b_0-\bar{a_0b_0},}$$を得て、さらにその相乗平均$${\bar{a_1b_1}＝\sqrt{a_1b_1}}$$を求める事で「±1」を「実数値」の範囲で繰り返す半径iの虚数円筒座標系に辿り着けます(Bipolar Spindle=二極紡錘体)。ここでいう「実数値」が「観測者自身が規約した計算精度」に従い、かつ「1」をどう定めるかも観測者の恣意に任せられている点に注意。

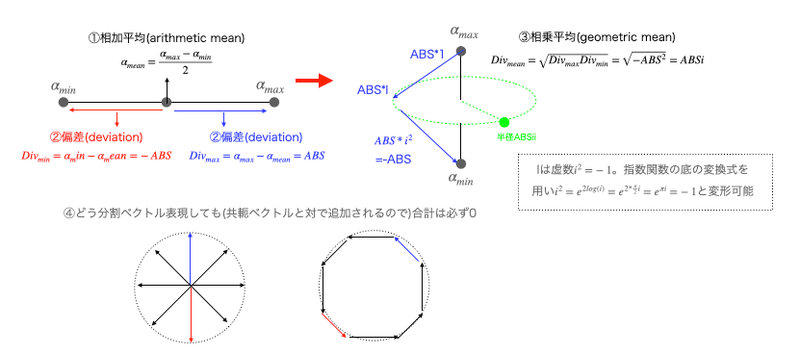
この変え方ではいきなり「ある実数値がその実数値を保つ乗法単位元1の直交バージョン」として最初からいきなり自明の場合としてそこに実存する虚数$${i^2=-1}$$…でも全然怖くなんてありません、指数関数における底の変換式$${a^b=e^{b*log(a)}}$$を用いると$${i^2=e^{2log(i)}=e^{2*\frac{π}{2}i}=e^{πi}=-1}$$でオイラーの等式$${e^{πi}=-1}$$そのもの。要するに「+1を-1に変換するには単位元0を中心に半周させてもよく、その場合の移動距離はπとなる」と言ってるだけなのですね。この半周分の周期は実数線上に存在せず、だから実数線上からはデフォルトではワープした様にしか観測出来ないから「虚数」。ただしオイラーの定理$${e^{θi}=cos(θ)+sin(θ)i}$$を用いれば線形分解によって実数値に対応する成分をcos(θ)という形で抽出する事が可能。「消化の原理を知らなくても人は食べて消化する」なる名言を後世に残した「叩き上げ電気技師」ヘヴィサイドが電気工学分野に援用して以降、その筋では必須教養となった筈。なおこのヘヴィサイドが導入したステップ関数こそが(機械学習概念の始祖)ニューロン・コンピューティングの最初期に導入された活性化関数で、あまりに使い勝手が悪いので「正義の関数シグモイドS」に差し替えられたりもしています。

なおネイピア数e(2.71828182…)には他にも面白い有効活用法が幾つもあるのですが、ここではそれが「穏やかな衰退($${α<1,\lim_{n→∞}α^n=0}$$)」と「幾何級数的増大($${α>1,\lim_{n→∞}α^n=0}$$)」の均衡点(直線的な等加速運動を等速円運動に変換する丁度良い数値)として現れる事さえ何となくイメージ出来てれば、とりあえずOKかと。

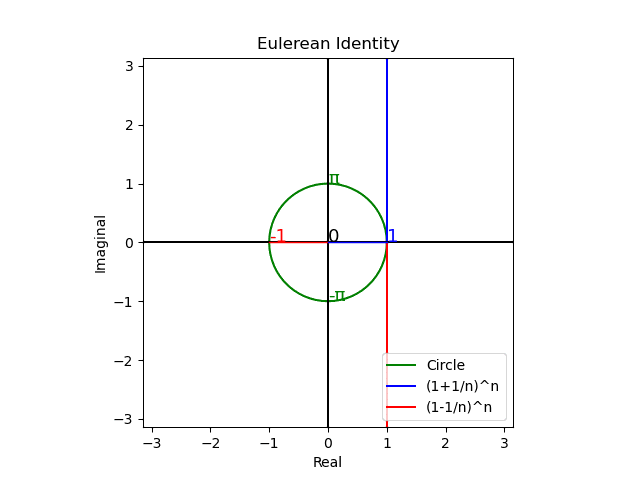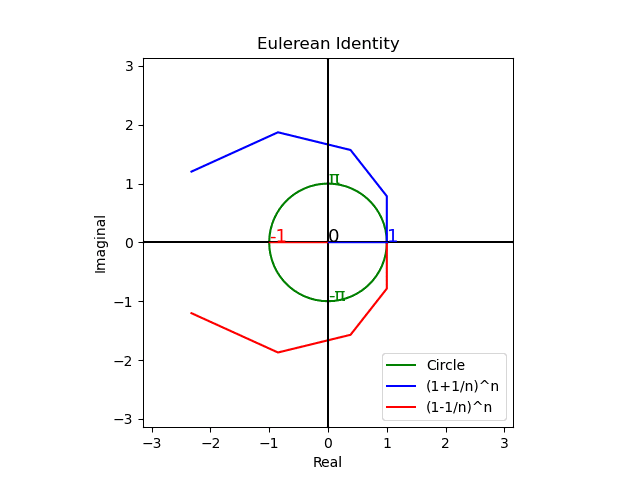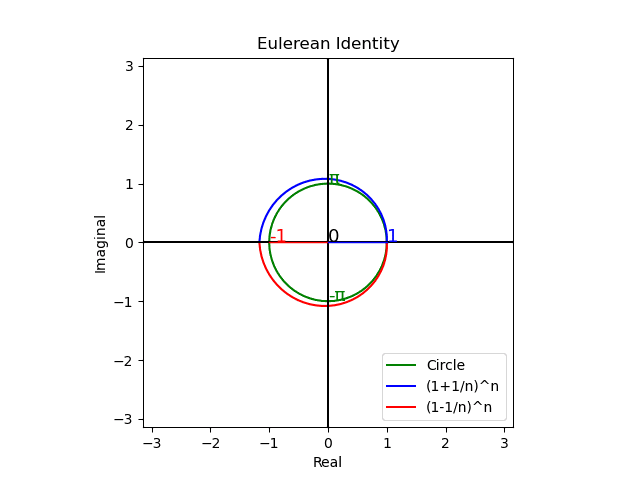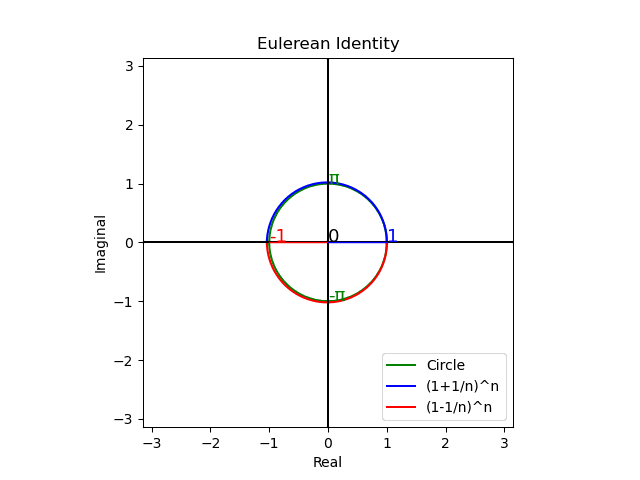
トーラス座標系で考える

ところで上掲の虚数円筒座標系は、実数線の+∞と-∞が不定極限$${\tilde{∞}}$$で交わり全体として円弧を描くと考えればトーラス座標系における「大半径1,小半径0の場合」に該当します。ここから出発して「大半径1,小半径1RPGの場合」を考えるとコンピューターRPGの様に「２次元平方眼だけで全空間が充填される単位トーラス座標系」に到達。これを「面=既知の２次元」と捉えると「点」とは上掲の二極紡錘体(Bipolar Spindle)を実数軸側から垂直に見下ろした複素平面Cos(θ)+Sin(θ)iならぬ純虚数平面Cos(θ)i+Sin(θ)jを指す事になりますね。私がここまでで何を語ったか理解出来た貴方、おめでとう!! 上掲の「連続する点(0次元)を束ねれば線(1次元)になり、連続する線を束ねれば面(2次元)となり、連続する面を束ねれば立体(3次元)となる」という考え方の原始的デカルト直交座標系イメージから仲良く一緒に卒業です!!

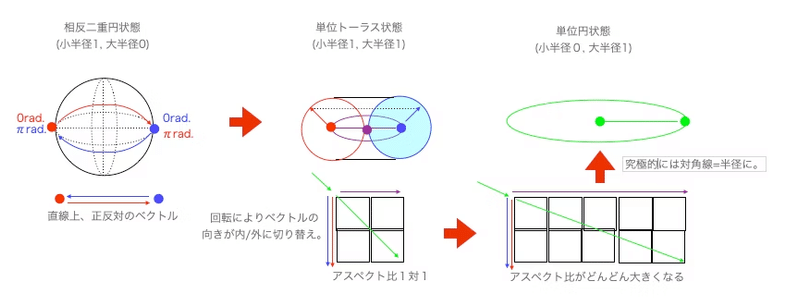
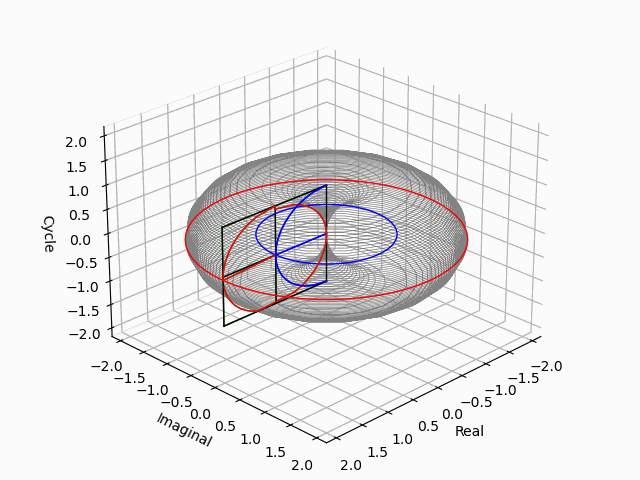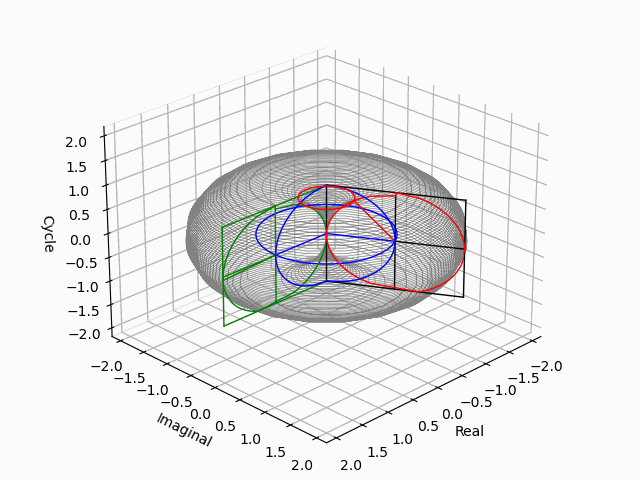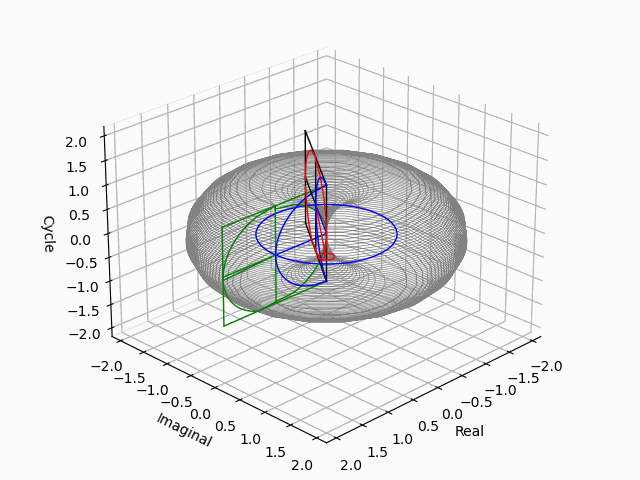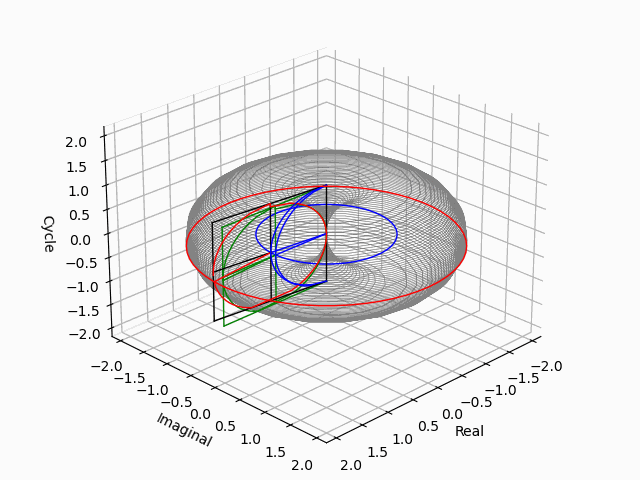
「第三軸をどう追加するか」問題

問題はこうして既に二つの軸が直交している状況で第三の軸がどう交わってくるか。この問題を解決するのが相関係数の考え方になってくる訳ですね。

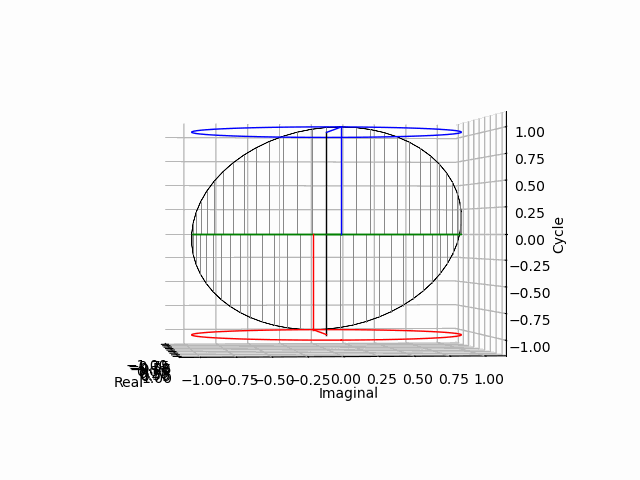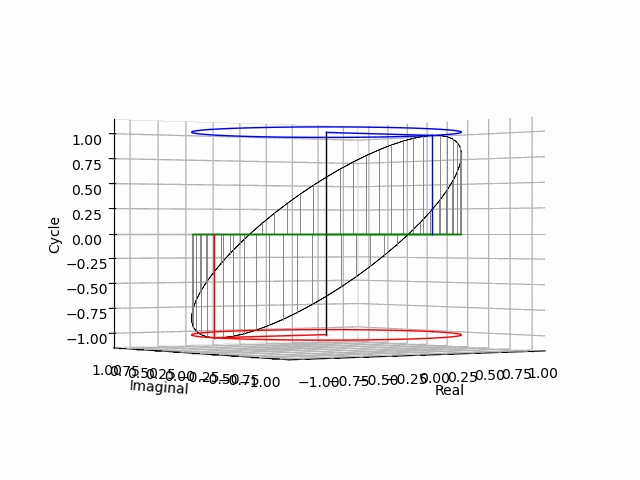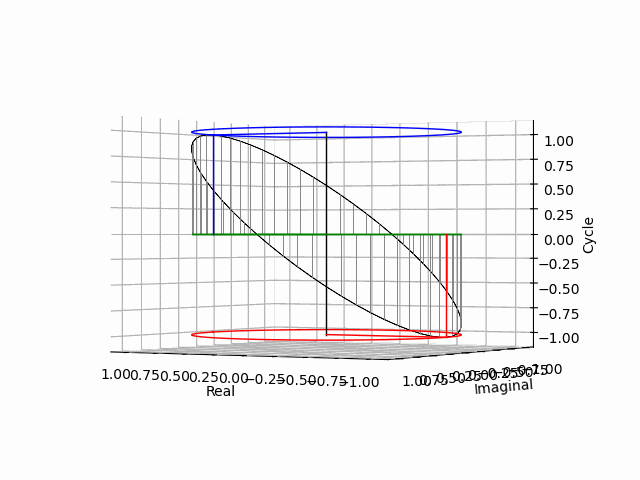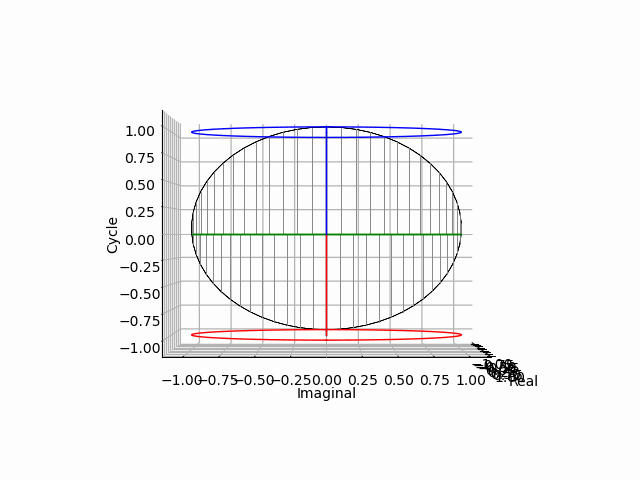
そうここで「点=二極紡錘体(Bipolar Spindle)を実数軸側から垂直に見下ろした場合の純虚数平面Cos(θ)i+Sin(θ)jの事」と規約した事が生きてくるのですね。「実数軸側から垂直に見下ろした場合=直交」という事はその前後もあるという話です。

本当の極限としての円数理

上掲の「カンブリア爆発期に生物が授かった視覚と視覚情報を処理する脊髄に由来する思考的限界」からほとんどの人類は三次元以上の空間認識を直感的に扱えません。数学的に厳密にいうと「数理の複雑さは導入する素数の数に比例するが、大半の人類がまともに扱えるのは精々"2"の全部と"3"の一部くらい」という事になる様です。もう"3"でさえ手一杯なのに"5"や"7"が追加された世界なんてとてもとても…

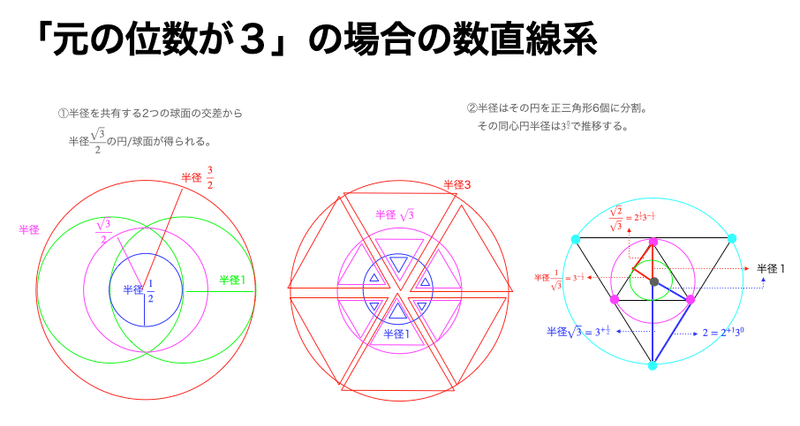
ああだから人類は「全く意思疎通が不可能な宇宙人」を描く時、その宇宙人が立拠する数字を"3"に設定したり…

"5"に設定したり…

"7"に設定したりしてきたのですね。

まぁ最新鋭言語と言って良いPythonですら３次元配列には手を出さない暮らしですから、この制約たるや絶対‥

その一方で人類は全ての途中をすっ飛ばしてN次元単極球面体(Unipolar Sphere)の研究に向かったのです。

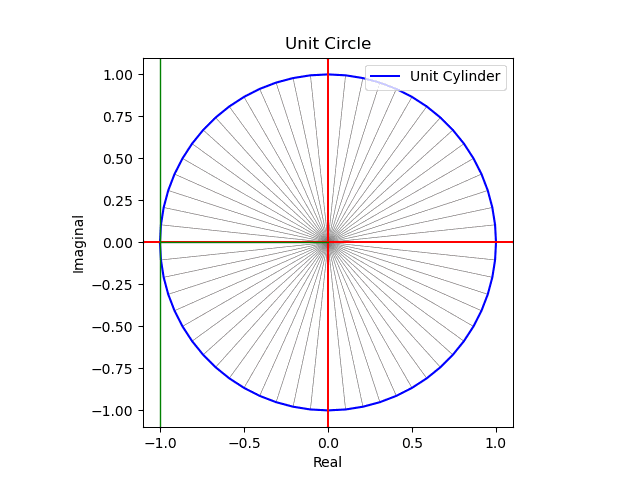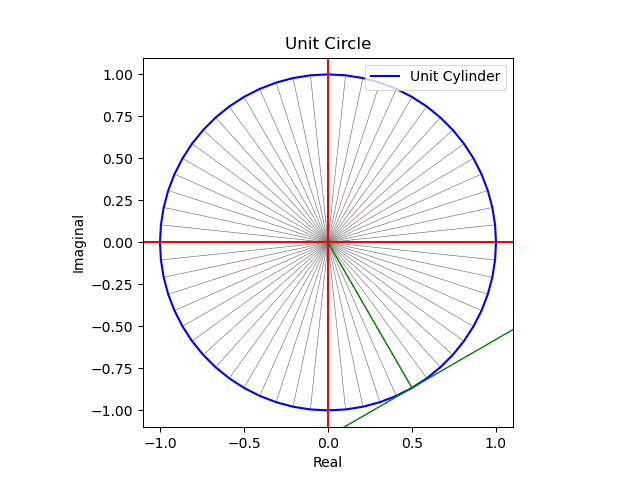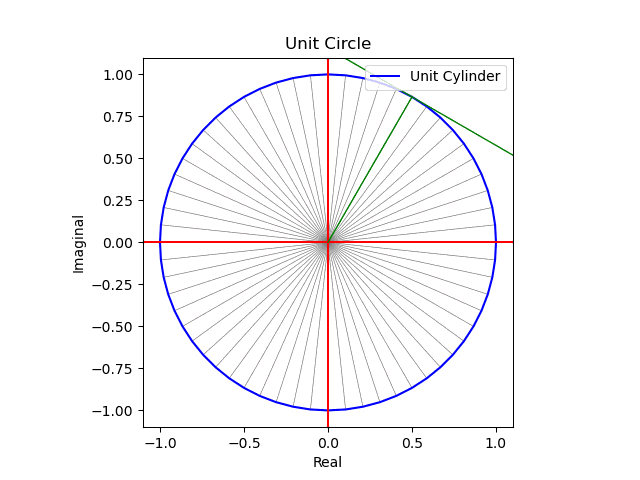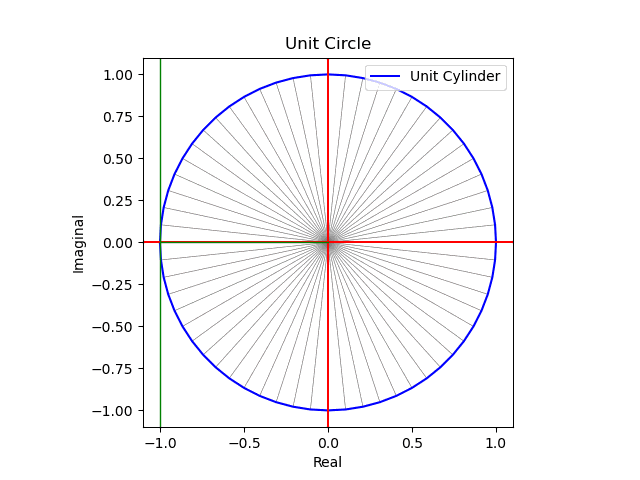
①その各半径は概ね各辺が1のN次元対角線であり、その距離は$${\sqrt{N}}$$で表される(N=∞と置けば、比率や交差角度に多少のバラツキがあっても相殺されてしまうと考える)。実際、固有の特徴を有する分布もサンプル数が増大するとその個性を失い正規分布に併合される事が多い。だと二項分布だと25以上、ポアソン分布だと5以上、t分布では30以上が目安とされる。

一般に標本分散でなく普遍分散の採用が推奨される目安がサンプル数3000前後。機械学習の世界でサンプル数がそれ以下という事はあり得ないのでpythonの統計ライブラリなどでは標本分散の使用がデフォルトとなっている。下手したら誤差扱いとも。

FM音源などはCos波(実数側)かSin波(虚数側)の足し合わせで三角波や鋸波や矩形波を合成するが、これを複素数領域全体で見るともう一つの軸に皺寄せが行っており、そうした偏り全体が視界を何処までも巨視的に拡大していく過程で必ずフラットラインしてしまう。そう、こちらもこちらでそういう形で「色即是空空即是色」の世界が広がっているという話。

②１次元上では符号のみ異なり絶対値が同じ実数値1対しか存在せず単位元=中心から下された垂線と垂直に交わる一方、自明の場合として水平には何とも接しない。2次元以上の任意の複素数2つは同様に単位元=中心から下された垂線と垂直に交わる一方、理論上隣接する範囲で水平に交わるがその範囲は極めて狭く、そもそも角度不定の状況なので比較共有可能な次元の抽出すら難しく概ね名義尺度のみ適用可能な集団に留まる。

ここでいわゆる確率論に出番が回ってきます。上掲の座標系では簡便化の為にデータ２値で「平均と分散の問題」を考えましたが、実際の運用状況では多数のデータからこれを割り出すのが普通ですね。

分散を求める際には「±の範囲に分布し合計すると0になる偏差集合」をそれぞれ2乗しますが、実はこの時「直径の世界(その一次元表現が両端開直線たるN次球面)」から「半径の世界(中心から球表面に伸ばされる各観測線をN次元対角線と見做す単極球面体)」への変換を行なっています。この時「分散幅が狭い」とは相関係数における+1寄り、すなわち単一評価軸への凝集性が高い事を指します。画像生成AIの出力でいうとこんな感じ。あたかも単一被写体の振る舞いをカメラで追ってるかの如き同一性の高さ。経験者の方ならお分かり頂けると思いますが、プロンプトを相当練り上げないとこうはなりません。
画像生成例

逆に「分散幅が広い」とは？最近画像生成AI投稿界隈では「オフショルセーター」なる概念が大流行なのですが、こちらに展開など各人が好き勝手改変を加えるせいで壮絶な展開を迎えていたりします(リンク先。ただしエロ注意)。

そう、学校の授業や教科書で触れる分散概念は「クラスの国語の小試験の成績のバラつき」みたいに単純な一次元分散だったと思いますが、実際には「単一評価軸への凝集」の反対は「多次元方向に向けての勝手な離散」。分析に際して分散分析やら分散共分散行列やら出てくるアレ。

こうして0(集合全ての元の値が同じ)から$${\tilde{♾️}}$$(任意の偏差があらゆる方向に向けて無秩序に及んだ状態)にかけて展開する分散概念は、自明の場合として非負の値しか取り得ません。あれ？それなら「負の相関係数」はどうイメージしたら…なんだかいきなり火薬臭い匂いが漂ってまいりました？

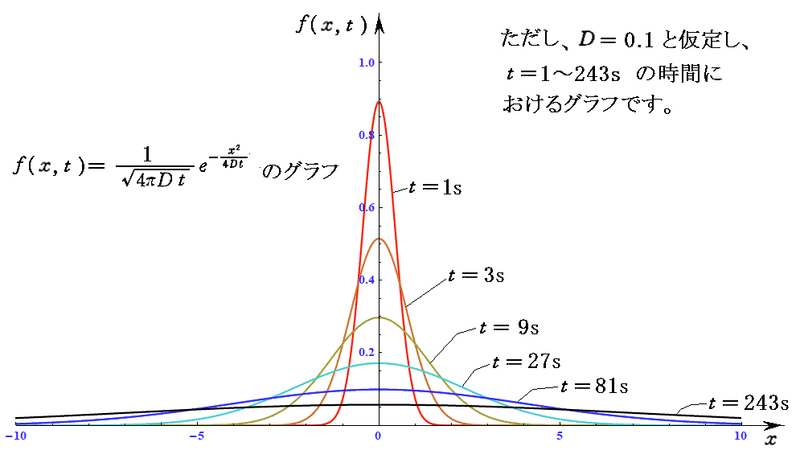
ここで実は人類はさらに危険な橋を渡ります。計算に必要な「何も起こってない時の分布」フーリエの熱伝導方程式に現れる様な物理現象に委ねたのです。今のところこの賭けは当たりで、どうやら概ねそれで正解である事が数多くの検証によって明らかとなったのです。

しかし21世紀に入ると人類は新たな謎に直面する事になりました。機械学習の成績がパラメーター数$${2^{10000}=10^{30}}$$を超えた前後より飛躍的に向上するのです。この現象についての説明は現時点では全く説明が見つかっていません。もはや「無限遠点からの声」が届いたとしか…

しかしまさにそういう「分布意味論の時代」だからこそ、トンネルを掘る際に反対側からも掘り進める様に「(恣意的に1を定める)主体側の在り方(最終的には適切な中心設定なしに適切な平均と分散は得られない)」もそれなりには追求されねばならないと思ってしまう訳です。

わちゃー、Qiita投稿ですら猫跨ぎ必至のフルスロットル状態に。まぁ「こういう思想を背景に色々考えてます」というOS解説書みたいな話に過ぎないので、この投稿自体は読み飛ばされても仕方がありませんね。