§８．１　仮想仕事の原理

解析力学は、ニュートンの３法則とは異なる原理で運動を解析し、運動に対するもっと広い視点を養うことを目指す。（これから習う物理につながっていく。）

つり合いの状態では合力がゼロ

であり、つり合った状態で仮想的に

動かすことを考える。（つり合っているのでひとりでに動くことはないから、仮想的である。）このときの仮想仕事について

が成り立つ。なぜならばF=0であったからである。これを仮想仕事の原理と呼ぶ。

仮想仕事の原理は、以下の例のように、拘束条件がある場合（つまりδrが自由に選べない場合）に力のつり合いを解くのに便利である。

例１：下図のように、円環上を動く質点を考える。

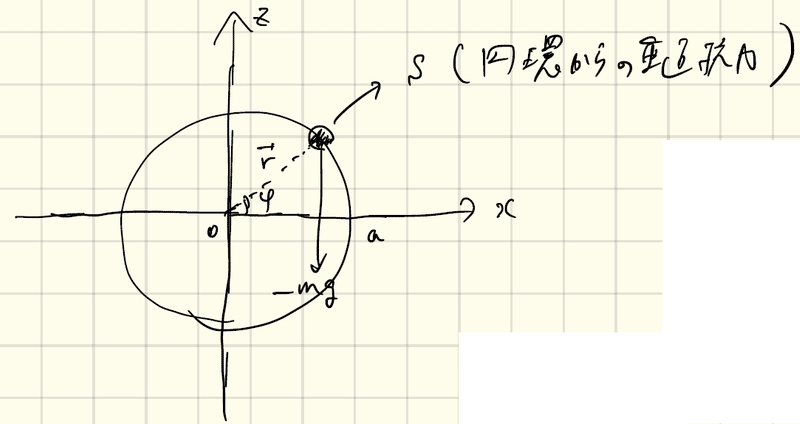
質点は、重力に加えて円環から垂直抗力Sを受ける。円環上に運動が制限されるので、仮想仕事は、

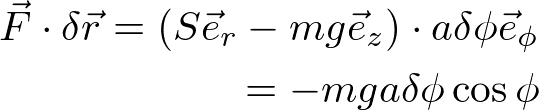
これがゼロになるときがつり合いであり、それは、Φ=90°、270°のときである。円環の一番下か一番上にいるとき（重力と仮想変位が垂直になるとき）がつり合いの条件であり、上記の答えは直感に合う。

例２：§７でも取り上げた、摩擦のない床でつり合っている棒を考える（下図）。

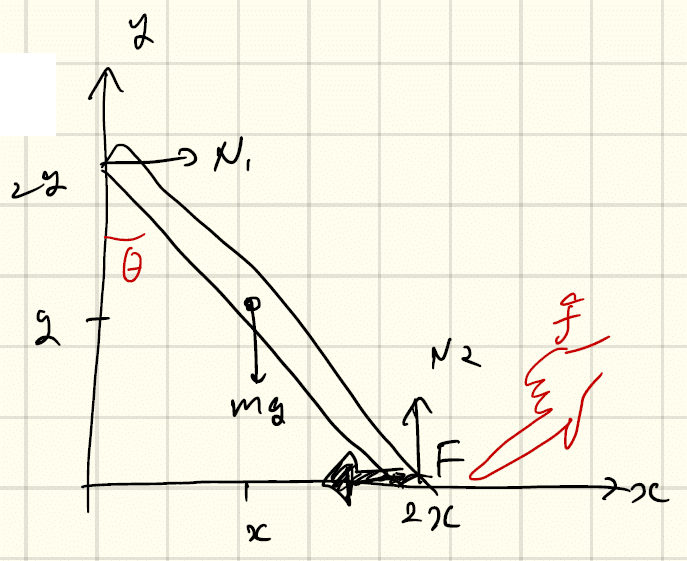
つり合っているときのFの大きさを求めよう。図のように(x,y)座標をとると、棒の長さLは、

と表せる。棒の仮想変位として(x, y)が(x+δx, y+δy)に変位したときの仮想仕事を計算する。

まず、棒が壁と床に接したまま仮想的に移動するということは拘束条件として

が成り立つ。この式は(x,y)が半径L/2の円上に拘束されることを意味し、仮想変位はこの円の動径方向(x,y)に直交するので

を満たす。仮想仕事は、手（力F)が棒にする仮想仕事と重力が棒にする仮想仕事の和であり、

と書ける。以上より、δyを消去すると

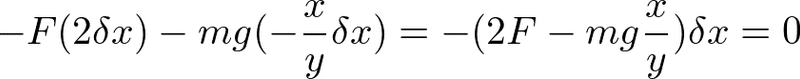
となるので、つり合いの条件は

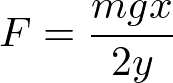
と求まる。もし図中の角度θを用いて表現すると、

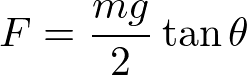
となり、前節で求めた結果と一致する。このように、力のモーメントを考慮せずにつり合いの条件を求めることができる。垂直抗力が出てこないという点では簡単といえる。

§８．２　ダランベールの原理

仮想仕事の原理は、静止している質点のつり合いを与える原理であった。運動している質点を記述する力学の原理を、ダランベールの原理という。

を変形して

とし、第二項を慣性力とみなせば、形式的に仮想仕事の原理を適用できる。つまり、ダランベールの原理は、

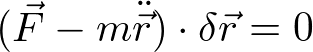
である。ダランベールの原理も、拘束条件がある場合に便利である。

§８．３　ラグランジュの運動方程式

保存力F=-∇U(r)がはたらく運動を考える。

と書き表すことができるので、ダランベールの原理より

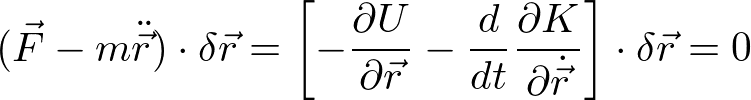
となる。ここで、Kは運動エネルギー

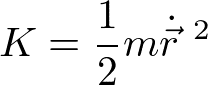
である。つり合いのときに、[ ]内がゼロになる。

ラグランジアン

を定義する。Lは

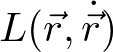
であり、位置と速度の関数である。位置と速度を独立変数とみなしていることに注意する。Kは速度のみを含み、Uは位置のみを含むことから

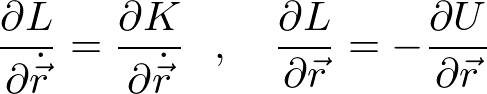
であるので、ダランベールの原理の式から

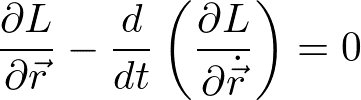
を得る。これをラグランジュの運動方程式と呼ぶ。

問８．１　ラグランジアンとして

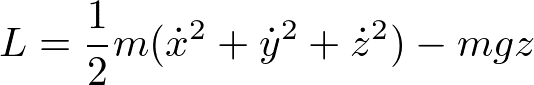
ととるとき、ラグランジュの運動方程式を計算せよ。

一つの利点として、ラグランジュの運動方程式は座標系によらずに同じ形になる。一般に、

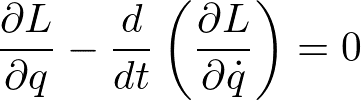
である。qは一般座標であり、運動を記述する自由度で長さの次元をもつとは限らない。また、ニュートンの運動方程式と異なり、一階の時間微分しか含まない運動方程式になっている。

例：振り子

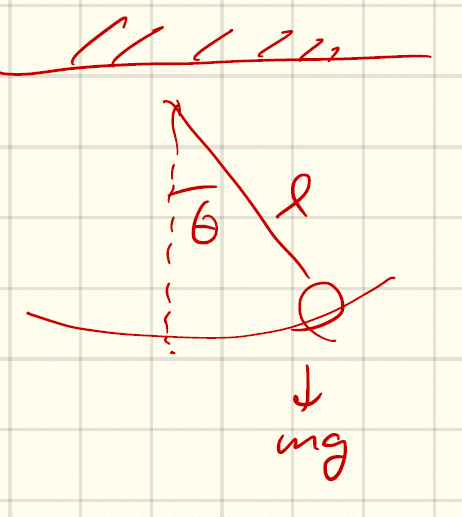
糸はぴんと張っているので、運動を記述する自由度である一般座標は角度θの一つでよい（図参照）。運動エネルギーは

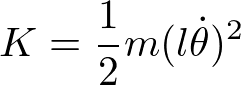
であり、ポテンシャルエネルギーは（止まっているときの最下点から考えて）

なので、ラグランジアンは

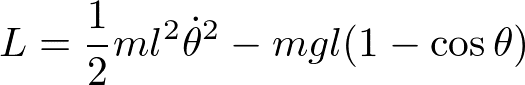
である。ラグランジュの運動方程式

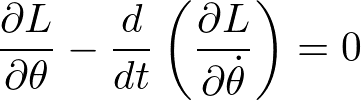
に代入すると、

よって、

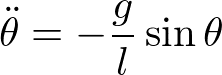
が得られる。このように、糸の張力を考慮することなしに運動方程式が得られる。

直交座標を用いた場合と極座標を用いた場合のラグランジュの運動方程式を比較してみる。ラグランジアン

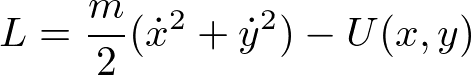
を、運動方程式

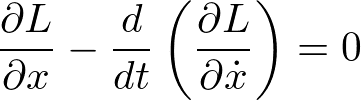
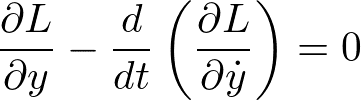
に代入すると、

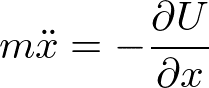
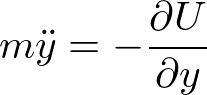
とニュートンの運動方程式と同じ形を得る。一方、極座標表示では、ラグランジアン

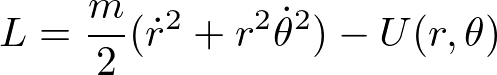
を運動方程式

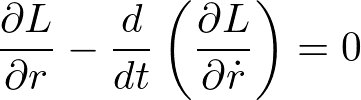
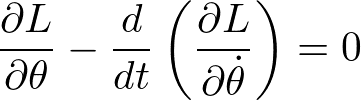
に代入すると、

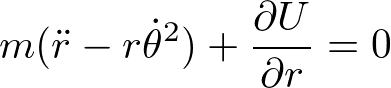
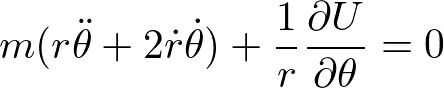
を得る。座標系を変換する計算を頑張って行わなくても自動的に極座標系の運動方程式が得られることがわかる。

§８．４　ハミルトンの原理

変分原理とは、”何かの積分”が極大or極小になるような経路が自然界で選ばれるという考え方のことである。”何かの積分”を作用と呼ぶ。物理学における最大の指導原理の一つで、ニュートンの法則はここから導かれる。点Aから点Bに質点が移動するときに、これまでは質点の運動を運動方程式を使って求めていたが、本節での主役は経路になる。どのような経路でAからBに向かうかを考えたときに、作用が最小になる経路が実際の運動として選ばれる（最小作用の原理）。

作用はラグランジアンを用いて

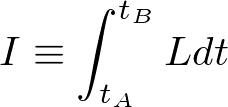
と定義される。Aにいる時刻t_AからBに到達する時刻t_Bまでの積分である。この作用が極値をとる経路が実際のAからBまでの運動経路であり、その条件は

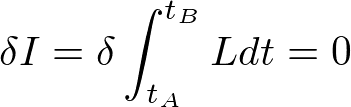
である。AとBを固定した上で経路が少しずれたときのずれδIである。

ラグランジアンが

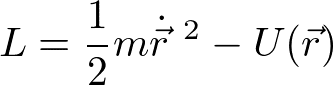
のとき、ラグランジアンは位置と速度の関数であり、rがr+δrに微小変位するとしてδIを計算すると、

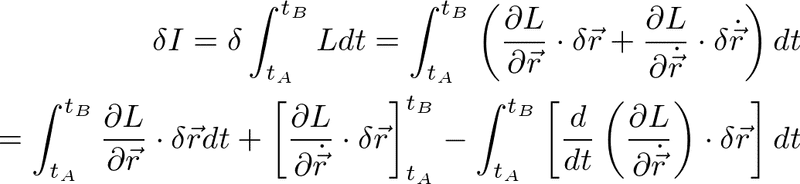
となり、AとBでδrがゼロとする（固定されている）とすると、

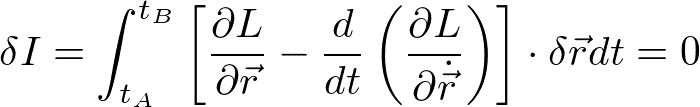
となり、ラグランジュの運動方程式が得られる。ラグランジュの運動方程式が成立する経路が自然界で選ばれていることになる。

§８．５　保存則と対称性

（１）エネルギー保存則

普段意識しないが、時間の原点は任意にとれる。これは時間に対する並進対称性があることを意味する。ラグランジアンの言葉でいうと、ラグランジアンが位置と速度を通じて時間に依存しており、あらわに時間によらない。もしラグランジアンが時間にあらわに依存すると、つまり

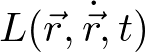
だとすると、t→t+δtの変化により、Lは変化してしまう(並進対称性がない）。

ラグランジアンが時間にあらわによらないとき、

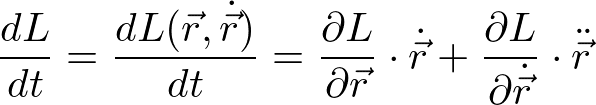
ラグランジュの運動方程式より

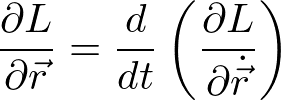
なので、代入すると

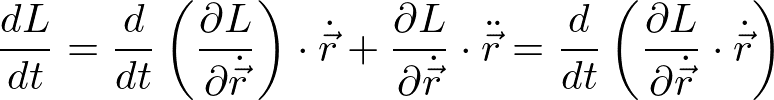
を得る。よって、

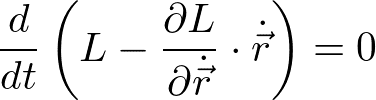
となり、( )内が保存量になる。Lが

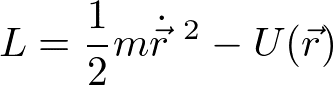
のとき、（ ）内は

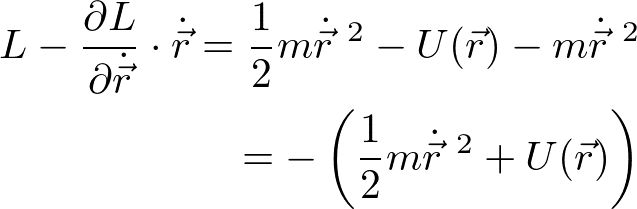
となり、力学的エネルギーの保存則を表す。以上により、ラグランジアンがあらわに時間によらない場合は、時間の並進対称性があり（ラグランジアンが時間の原点のとり方によらず）、力学的エネルギーが保存する。

（２）運動量保存則

ラグランジアンが並進対称性をもつとき、つまり、r→r+δrでラグランジアンが変わらないとする。

運動方程式の解の経路から経路をδrだけ並進したとき、

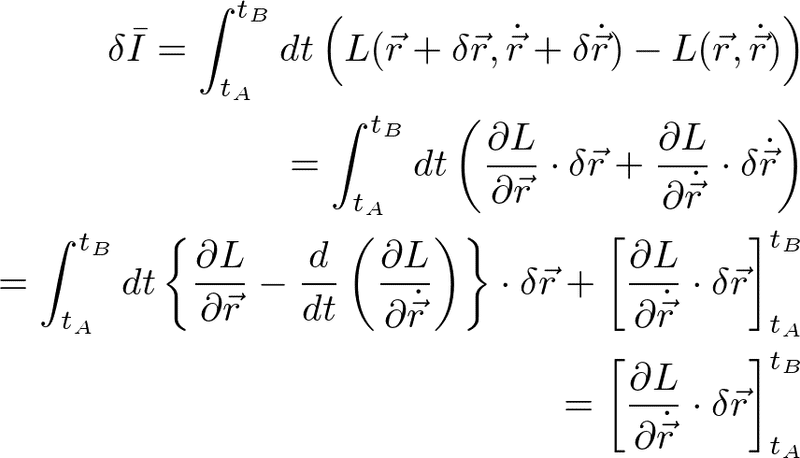
である。ここで、ラグランジュの運動方程式を使った。ここではAとBは固定端ではないので端も含めてδrだけ一様に並進している。並進対称性がある場合は、上式がゼロになる。よって、Lが

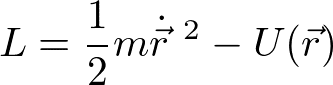
のときには、

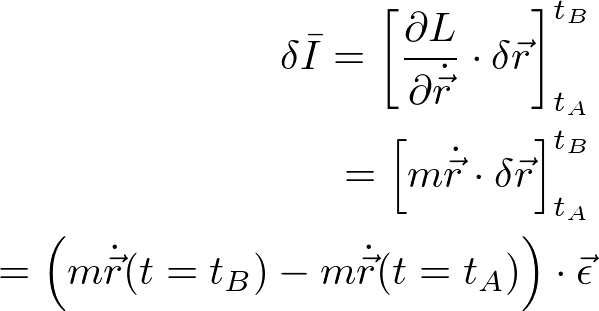
と書き直せる。ここで、経路全体を微小変位εだけ一斉に並進していると書きなおした。以上より、並進対称性がある場合には上式がゼロになり、運動量が保存することがわかる。

（３）角運動量保存則

回転対称性がある場合、つまり回転に対してラグランジアンが不変な場合は、角運動量が保存する。

回転軸方向を向くベクトルδΦを用いて、微小変位は

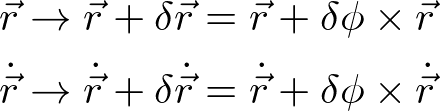
と表せるので、運動量保存則のときと同じようにして、経路の微小変位に対する作用の変化は

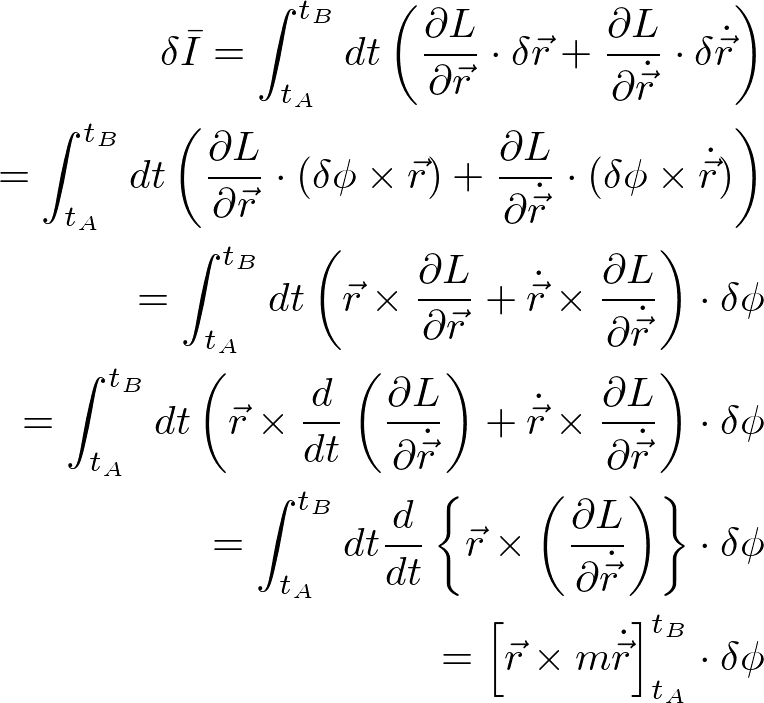
と計算できる。途中でラグランジュの運動方程式を使っている。回転対称性があれば、上式がゼロになる。[ ]内は角運動量であり、この式は角運動量保存の法則を表している。

以上の（１）～（３）でみたように、保存則は個々の力学系の性質には無関係で、時空間の対称性に起因する、より本質的な保存量である。このことはニュートンの運動方程式からではわからないことである。