巷で話題のベイズ統計学。その理論の中核となっているのがベイズの定理です。
「名前は知っているけど何がすごいの？」
「従来の統計学との違いは？」
そんな疑問をお持ちの方も多いのではないでしょうか。
でも大丈夫！このシリーズでは、身近な例を通してベイズ統計学を基礎から解説していきます。数式を抑えて直感的に理解できるような構成ですので数学にニガテ意識があっても読み進めていただけます！

※「理解できる」と「実際に使える」はちょっと違います。もしこのシリーズを読んでもっと深く勉強したいと思った方は参考書籍記事（準備中）を読んでみてください。
また、定義式は書かざるを得ないので、厳密には数式（ほぼ）ゼロの解説です。

【準備】：今回使う記号

はじめに、下準備として今回の記事で用いる記号を２つ紹介していきます。確率について高校範囲まで問題ない方は本編へ進んでください！

記号その①　P(A)・・・Aが起こる確率

例としてオモテとウラが等しい確率（それぞれ1/2）で出るコイントスを考えましょう。オモテが1/2の確率で出ることをこの記号で表現したい場合、以下のようになります。

P(オモテ) = 1/2

また、起こりうる出来事（事象と呼びます）の確率P()を全て足し合わせると１になります。コイントスでは「オモテ」と「ウラ」が起こりうる全ての事象ですので、

P(オモテ) + P(ウラ) = 1

となります。この式は、オモテとウラのどっちかが出る確率は１だということを表しています。

記号その②　P(A|B)・・・Bという条件の時にAが起こる確率

今度はコイントスを何回か行い全てオモテがでる確率を考えましょう。先ほどのP()記号を用いると、

P(コイントスをX回行って全てオモテ)

と表現できます。Xが１のとき、この確率は先ほどの例と同じ1/2となります。しかしXが増えれば増えるほどに「全てオモテ」の確率は小さくなっていきます。たくさんコイントスを行って、全てオモテを出すほうが難しいのは当然ですね。
言い方を変えれば、「全てオモテ」の確率は「投げる回数」という条件で変化するとも捉えられます。記号その②を用いて表すと、

P(全てオモテ｜X回投げる)

となります。このような、「｜」の後ろに条件がついている確率を「条件付き確率」と呼びます。条件がつくと、より限定的に、時に具体的に確率を考えることができます。

今回使う記号は以上の２つです。この確率を「どのように求めるか」は今回は重要ではありません。「何を意味しているか」を掴んでいただけたら、安心して本編①に進んでください！

【本編①】：映画館は混んでいるだろうか？

皆さんは映画館に映画を観に行くことがありますか？DVDやAmazon Primeも手軽で良いですが、大きなスクリーンで楽しむのもなかなか良いものです。
東京に暮らすエイコさんは話題作『劇場版コード・ブルー　－ドクターヘリ緊急救命－』を観にいこうと考えています。しかしこのエイコさん、人混みは大のニガテ。なるべく空いている時に観に行きたいと思っています。
そこでエイコさんは混雑を避けるため、以下のような確率を予想し、混んでいる確率が小さいと予想できれば映画に出かけることにしました。

P(映画館が混雑している)

この確率は、とても広い意味での確率です。
混雑具合は、「レディースデーかどうか」や「公開からどのくらい時間が経過しているか」など、色々な要因に左右されることが予想できますが、それらを一旦横に置いて「だいたいこんなもんじゃないか」という感じで予想したものだと考えましょう。
エイコさんは「混んでいるかなんて、行ってみなければわからないよ」と思い、確率を以下のように予想しました。

P(映画館が混雑している)=1/2

※ここでの確率は、映画館の混雑率ではないことに注意してください。あくまで混雑しているかどうかの確率です。
エイコさんが混んでいると感じる確率が1/2であることを表し、50%の席が埋まっていることを表している訳ではありません。

※説明の便宜上1/2という確率を設定しましたが、今回は具体的な数字で確率を計算しません。

【本編②】：日曜日じゃないか！

十分な情報がないから偏りのない1/2という確率を採用したエイコさんですが、映画館に行かなくてもわかる、混雑度合いに影響する情報に気づきました。

「映画館が混んでいるかは曜日によって異なるのではないか」

そこで今日の曜日を確認することにしました。ムムム、今日は日曜日でした。なんだか混んでいそうです。エイコさんは日曜日という情報を得ることができました。ここからは、

P(映画館が混んでいる｜日曜日)

を考えていきます。条件付き確率ですね。ここでの状況は以下のように整理できます。

エイコさんは漠然とした確率から、日曜日という情報を得た後の確率へと予想を「更新」したのです。以下では、情報を得る前の確率を「事前確率」、情報を得た後の確率を「事後確率」と呼ぶことにします。

この更新は「ベイズ更新」と呼ばれます。ベイズ更新とは、これすなわち新しい情報を元に確率（予想）をより良いものにしていく学習です！非常に人間の思考プロセスに似ている気がします。

ここでようやく「ベイズ」という言葉が登場しました。これには「ベイズの定理」が関係しています。

【本編③】ベイズの定理登場

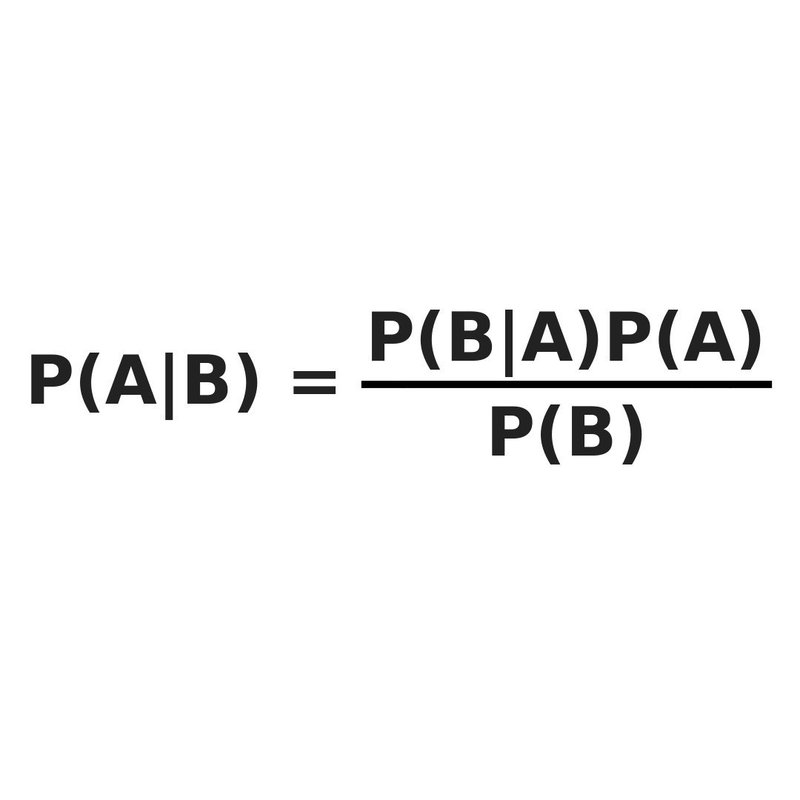
ばばん！こちらがベイズの定理です。AとBだとイメージしづらいので、これまで考えてきた映画館の確率に書き換えましょう。

左辺は事後確率（日曜日に映画館が混んでいる確率）です。右辺の分子には事前確率(混雑している確率)の姿が見受けられますね。

そうなのです、ずばりベイズの定理とは

事前確率と事後確率の関係性を表している

のです。

【本編④】尤もらしさ

先ほど、ベイズの定理とは事前確率に「何かしらの確率」をかけると事後確率となるという関係性を表していると述べました。ここではその「何かしらの確率」について考えていきます。

P(日曜｜混雑)

見たままで解釈すると「混雑していることがわかっている時に日曜日である確率」を表すことになります。
より直感的な言葉で言い換えれば

「日曜日に混雑していることが経験上どのくらいの割合で起こったか」

の確率としても解釈できます。少々ややこしいので、図を使って整理していきましょう。

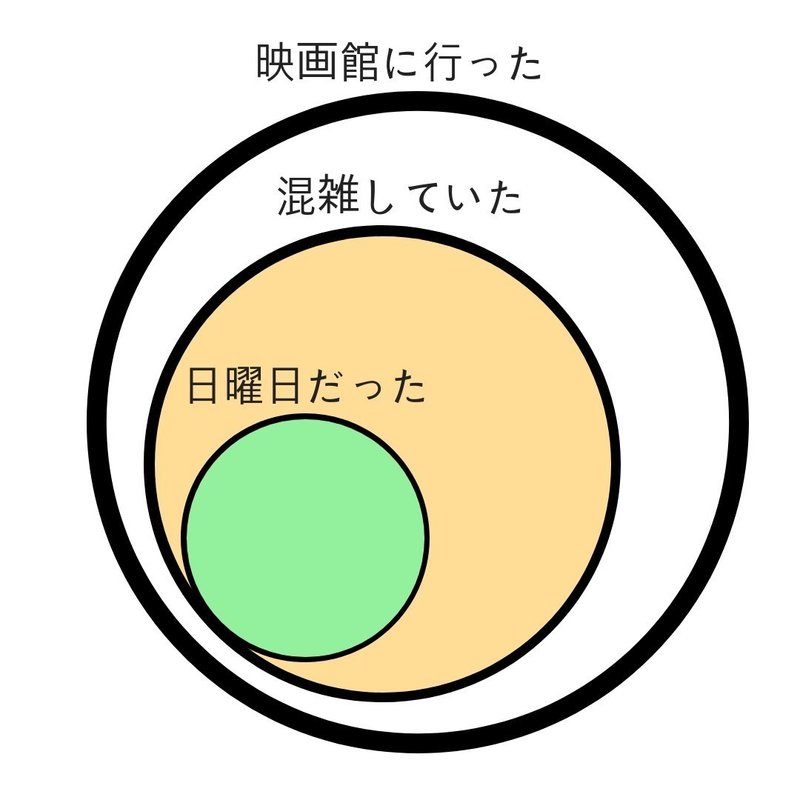
「映画館が混んでいる」という条件を得ているので、オレンジの円を分母として考えます。その中で日曜日だった確率なので「グリーン/オレンジ」で尤度が求まります。尤度の特徴として大切なのは、エイコさんの経験上得られる確率であるということです。これを念頭に置いてベイズの定理をもう一度確認しましょう。

【本編まとめ】ベイズの定理とは

なんと、「事前確率」に経験から得られる「尤度」をかけることによって「事後確率」が導かれています！

ベイズの定理とは、

事前確率（予想）に尤度（経験）を掛け合わせることで事後確率（経験に基づく予想）を求めることができる！

ことを表した定理なのです！

※右辺の分母にあるP(日曜)について気になった方もいらっしゃるかもしれません。この項は、数学の都合でくっついている解釈上深い意味のない項です。
確率は全て足すと１にならないといけません。その条件を満たすためにこのような定数（正規化定数と呼びます）をかけているのです。数学的に込み入った話になるので解説するとしたらだいぶ後になると思います。

【次回予告】

次回はこのベイズの定理を使って具体的に問題を解いていきます。また、この公式の導出も行います。