前回の続きから書いていきます。
　前回の記事はこちら↓↓

１　問題の確認

問題

1. 原始ピタゴラス数は{3,4,5}の他にもあるのか。あるなら具体例を示せ。

2. 原始ピタゴラス数は無数にあるのか。あるなら生成する式を、ないならばそれを証明せよ。

２　前回の記事で見いだしたこと

　最初に一辺の長さが$${n}$$の正方形があったとする。
　この正方形の周りにペットボトルキャップを付け加えたとき、第$${k}$$層のキャップの数と正方形のキャップの個数が一致すれば、必ず正方形を作ることができる。（図１）

３　k層のキャップの数は？

　図１のオレンジの〇（キャップ）の数は
　$${n×n=n^2}$$（個）

　では、$${k}$$層の〇（キャップ）の数を$${k}$$で表せると、図１に書いた【正方形を作れる条件】の式に当てはめて、原始ピタゴラス数が作れそうです。

　$${k}$$層の〇（キャップ）の数を求めるには、まず１層、２層、３層のキャップの変化を確認します。

　１層のキャップの個数は、
　$${2×n+1=2n+1}$$（個）

　２層のキャップの個数は、
　$${2×n+3=2n+3}$$（個）

　同様に考えると、
　３層　$${2n+5}$$
　４層　$${2n+7}$$
　５層　$${2n+9}$$

　このことから、$${k}$$層のキャップの個数は、
　$${2n+2k-1}$$（個）といえる。

４　正方形を作れる条件の式に代入

　正方形を作れる条件式は、以下の通りでした。

　オレンジの〇の数は$${n^2}$$、$${k}$$層の〇の数は$${2n+2k-1}$$なので、
　$${n^2=2n+2k-1}$$
　$${n}$$について解くと、
　$${n^2-2n-2k+1=0}$$
　解の公式を使って、
　$${n=1±\sqrt{1^2-1×(-2k+1)}}$$
　　$${=1±\sqrt{2k}}$$
　$${n>0}$$より、
　$${n=1+\sqrt{2k}}$$

　また、$${n}$$は自然数なので、$${k=2j^2}$$となる自然数$${j}$$を用いれば、
　$${n=1+\sqrt{2k}}$$
　　$${=1+\sqrt{4j^2}}$$
　　$${=1+2j}$$　・・・①

５　原始ピタゴラス数を求める

　上で使っていた$${n}$$や$${k}$$は、三平方の定理の$${a,b,c}$$のいずれを表すのか、おさらいです。

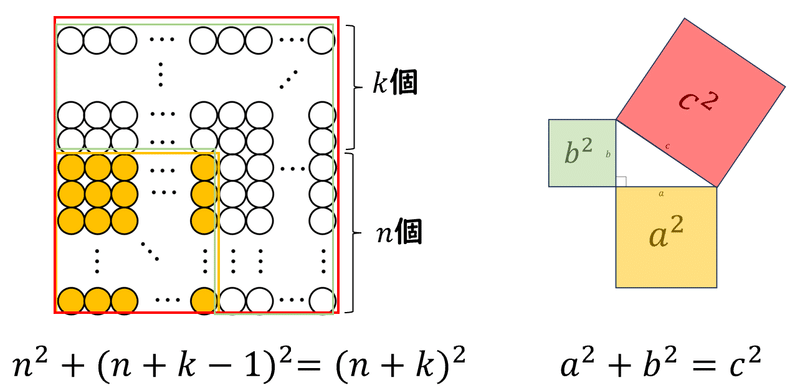
　$${b}$$と$${n+k-1}$$の対応についても、再掲しておきます。
　そもそも、このように最も外側の$${k}$$層のキャップを移動させて隙間を埋めて正方形をつくることを考えているからでした。

　$${j=1}$$のとき、
　$${n=1+2×1=3}$$
　$${k=2×1^2=2}$$
　よって、
　$${n+k-1=3+2-1=4}$$
　$${n+k=3+2=5}$$

　よって、原始ピタゴラス数$${(3,4,5)}$$ができた。

　$${j=2}$$のとき、
　$${n=1+2×2=5}$$
　$${k=2×2^2=8}$$
　よって、
　$${n+k-1=5+8-1=12}$$
　$${n+k=5+8=13}$$

　よって、2つ目の原始ピタゴラス数$${(5,12,13)}$$ができた。
　実際に確かめてみると、
　$${5^2=25,12^2=144,13^2=169}$$
　だから、
　$${25+144=169}$$

　$${j}$$を、３～２０に変化させたときの原始ピタゴラス数の一覧は以下の通りです。

　これで、問題の解答ができました。

６　問題の解答

問題

1. 原始ピタゴラス数は{3,4,5}の他にもあるのか。あるなら具体例を示せ。

2. 原始ピタゴラス数は無数にあるのか。あるなら生成する式を、ないならばそれを証明せよ。

１の解答
　原始ピタゴラス数$${(5,12,13)}$$が存在する。

２の解答
　$${j}$$を自然数とする。
　$${n=1+2j,k=2j^2}$$のとき、
　$${(n,n+k-1,n+k)}$$は原始ピタゴラス数になる。

７　考察

　上述したように、原始ピタゴラス数が無限に存在することや、その生成式をつくることができました。

　では、この式で漏れなく原始ピタゴラス数を生成できるのでしょうか？

　残念ながら、答えはNOです。

　例えば、原始ピタゴラス数に$${8,15,17}$$が存在しますが、上述した表にはありません。

　なぜ生成できなかったのか。

　それは、今回見つけた生成式
　$${n^2+(n+k-1)^2=(n+k)^2}$$
　の後ろ２つの項に原因があります。
　$${n+k-1}$$と$${n+k}$$は連続する整数なので、そういう場合の原始ピタゴラス数しか生成できないのです。
　よって、$${8,15,17}$$のようなものの生成ができなかったというわけです。

８　おわりに

　今回、原始ピタゴラス数の完全な生成式を導くことはできませんでした。
　それがペットボトルキャップで可能なのか、気になりますね。

　最後まで読んでいただきありがとうございました！！