１　はじめに

　突然ですが、質問です！！
　面積が１の正三角形があります。この正三角形に次の操作を、次々にしていきます。
（操作）
　操作する前の正三角形の各辺の三等分点を頂点にもつ正三角形を、操作する前の正三角形の外側に付け加える。

　操作を続けていくと、図形の面積はどうなると思いますか？

A　無限に大きくなる　　　
B　無限に大きくならない

　この記事では、操作を続けていった図形の面積の行きつくのは何なのか？この問いに関わる古代ギリシャにおけるゼノンのパラドックスを前編で紹介します。後編で、上の問いの答えを導きます。最後に、このような操作をしていってできる図形を研究する数学の一分野を紹介します。
　最後まで読んでいただければ嬉しいです。

２　そもそも辺の三等分は可能なのか？

　数学の図形の問題では、よく「角を二等分して、～を点Pとする」のように作図があります。
　これは私がよく思うのですが、その作図はできるのか？ということです。ではこの問題では、辺を三等分する作図をします。これはできます。
①　適当な長さの線分BCをかきます。
②　線分BCと同じ長さの線分CD、DEをかきます。
③　線分AEをかきます。
④　AEと平行な直線を点Cを通るようにかき、辺ABとの交点を点Fとします。
⑤　AEと平行な直線を点Dを通るようにかき、辺ABとの交点を点Gとします。
　この点F、Gが辺ABを三等分する点です。

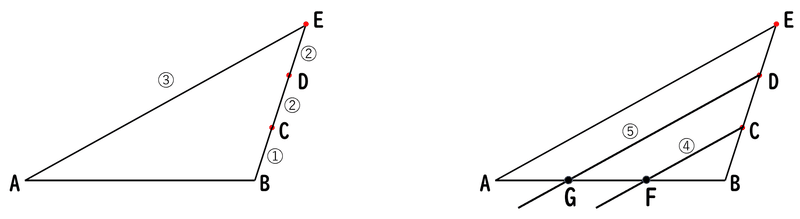
　なぜ点F、Gが辺ABを三等分する点か説明します。
　△ABEと△FBCで、
　∠Bは共通・・・（ア）
　AE//CFより、平行線の同位角は等しいから、
　∠AEB=∠FCB・・・（イ）
　２組の角がそれぞれ等しいので、
　△ABE∽△FBC
　相似な図形では、対応する辺の比はそれぞれ等しいので、
　BC:BE=BF:BA=1:3
　同様の証明で、
　BD:BE=BG:BA=2:3
　よって、点F、Gが辺ABを三等分する点と説明できました。
　ちなみに、角の三等分は直角を三等分するなど特殊な場合を除いてはできません。

３　どんな値になるの？パラドックスから考える

・　ゼノンのパラドックスとは

では次に、この題について考えます。これで有名なのは、ゼノンのパラドックスです。
　概要は次の通りです。
　A地点とB地点があります。A地点からB地点に向かって矢を放ちます。
　まずこの矢は、ABの半分、$${\frac{1}{2}}$$だけ進みます。
　次に残り$${\frac{1}{2}}$$の半分、$${\frac{1}{4}}$$だけ進みます。
　次にまた$${\frac{1}{4}}$$の半分の$${\frac{1}{8}}$$だけ進みます。
　このように、矢は残った距離の半分だけ進んでいくとすると、いつまで経ってもB地点まで着きません。でもそんなわけないですよね？矢はいつかはB地点に到達します。つまり間違っているのは、人間の考え方ですね！
このパラドックスで成り立ってほしいのは、次の式です。
$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…=1}$$

・　ゼノンのパラドックスの類似例で納得する

　面積が１の正方形があります。
　この正方形の半分の面積は、$${\frac{1}{2}}$$
　残りの半分の半分の面積は、$${\frac{1}{4}}$$
　残りの半分の半分の半分の面積は、$${\frac{1}{8}}$$

　もともと正方形の面積は１だから、
　$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…=1}$$
ということが直感的にいえそうです。

・　高校数学の範囲で理解する

$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…}$$の部分和を$${S_n}$$とします。
　このとき、

$${S_n= \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…(\frac{1}{2})^n}$$
この両辺を \frac{1}{2}倍して、
$${\frac{1}{2}S_n= \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…(\frac{1}{2})^{n+1}}$$

辺々ひくと、
$${\frac{1}{2}S_n = \frac{1}{2}-(\frac{1}{2})^{n+1}}$$
両辺に2をかけて、
$${S_n = 1-(\frac{1}{2})^n}$$

　この式は、$${n}$$番目までの和ですが、これを限りなく大きくしたときに、$${S_∞ = 1}$$となってほしいわけです。つまり、$${(\frac{1}{2})^n→0}$$となってほしいのです。$${n}$$が大きくなればなるほど、無視できるほど小さくなるので、これは直感的に言えそうですね。
　よって、
$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…=1}$$

・　εーN論法で厳密に理解する

　先ほど直感的に$${(\frac{1}{2})^n→0}$$はいえると申しましたが、これでは数学的に厳密ではありません。これを理解するには、大学で学ぶε‐N論法が必要です。かなり抽象的なので、理解できなくても大丈夫です。

ε‐N論法
　任意の正のεに対して、ある自然数Nが存在して、$${n}$$が$${n\geqq N}$$ならば、$${|a_n-α|<ε}$$となるとき、$${\lim_{n \to ∞}  a_n=α}$$となる。

　では、ε‐N論法で$${n\to ∞}$$のとき、$${(\frac{1}{2})^n→0}$$を示します。
　$${|a_n-0|<ε}$$に、$${a_n=(\frac{1}{2})^n}$$を代入して、
　$${|(\frac{1}{2})^n-0|<ε}$$
　$${(\frac{1}{2})^n<ε}$$
　両辺に自然対数をとって、
　$${\log (\frac{1}{2})^n<\log ε}$$
　$${n\log \frac{1}{2}<\log ε}$$
　$${-n\log 2<\log ε}$$
　両辺を$${-\log 2}$$でわる
　$${n>\frac{\log ε}{\log 2}}$$
　よって、どんな正の数εが与えられても、$${N>\frac{\log ε}{\log 2}}$$を満たすNが存在し、$${n\geqq N}$$とすれば、$${|a_n|<ε}$$が成り立つといえる。
　よって、$${(\frac{1}{2})^n→0}$$が証明されました。
　$${\frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+…=1}$$

４　おわりに

　今回の記事では、「１　はじめに」で述べた問題を解くための基礎知識を示しました。後編では、問題を解いていきます。
　最後まで読んでいただき、ありがとうございました！！