今回の統計トピック

確率変数$${x}$$と$${x+1}$$の２つの確率の比を計算します！
組み合わせ$${\ _nC_x}$$の公式、二項分布の確率質量関数をサクサクと分解して、確率の比の式を見つけます！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

確率分布の分野
問5 ２項確率の比（サイコロの目）

試験実施年月
統計検定2級 2018年11月 問9（回答番号14）

問題

公式問題集をご参照ください。

解き方

題意
二項分布の確率の比を計算します。

数式が並びます。心のご準備をお願いいたします。

$${\cfrac{P(X=x+1)}{P(X=x)}}$$に二項分布の確率質量関数を当てはめて、解きます。

$$
\begin{align*}
\cfrac{P(X=x+1)}{P(X=x)}&=\cfrac{_nC_{x+1} \ p^{x+1} \ (1-p)^{n-x-1}} {_nC_x  \ p^x \ (1-p)^{n-x}}\\
  \\
&=\cfrac{\cfrac{n \times n-1 \times \cdots \times n-x+1 \times n-x}{x+1 \times x \times \cdots \times 1}}{\cfrac{n\times n-1 \times \cdots \times n-x+1}{x \times \cdots \times 1 }}\times \cfrac{p^x\times p}{p^x} \times \cfrac{(1-p)^{n-x} \times (1-p)^{-1}}{(1-p)^{n-x}}\\
  \\
&=\cfrac{\cfrac{\cancel{n \times n-1 \times \cdots \times n-x+1} \times n-x}{x+1 \times \cancel{x \times \cdots \times 1}}}{\cfrac{\cancel{n\times n-1 \times \cdots \times n-x+1}}{\cancel{x \times \cdots \times 1} }}\times \cfrac{\cancel{p^x}\times p}{\cancel{p^x}} \times \cfrac{\cancel{(1-p)^{n-x}} \times (1-p)^{-1}}{\cancel{(1-p)^{n-x}}}\\
  \\
&=\cfrac{n-x}{x+1} \times p \times \cfrac{1}{1-p}\\
  \\
&=\cfrac{(n-x)p}{(x+1)(1-p)}
\end{align*}
$$

休憩タイムです。

上述の$${\cfrac{(n-x)p}{(x+1)(1-p)}}$$に試行回数$${n=7}$$と成功確率$${p=1/3}$$を当てはめます。

$$
\begin{align*}
\cfrac{P(X=x+1)}{P(X=x)}&=\cfrac{(n-x)p}{(x+1)(1-p)}\\
  \\
&=\cfrac{(7-x)\times 1/3}{(x+1)(1-1/3)}\\
  \\
&=\cfrac{(7-x)\times 1/3}{(x+1) \times 2/3}\\
  \\
&=\cfrac{7-x}{(x+1) \times 2}\\
  \\
&=\cfrac{-x+7}{2x+2}
\end{align*}
$$

$${\cfrac{P(X=x+1)}{P(X=x)}=\cfrac{-x+a}{2x+b}}$$の$${a,b}$$は$${a=7, b=2}$$です。

問題文のサイコロの試行が二項分布に従うことを見つけて、二項分布の確率質量関数を当てはめて、ゴリゴリ数式をほぐす、こんな感じでした。

解答

② $${a=7,\quad b=2}$$ です。

難易度　ふつう

・知識：二項分布の確率質量関数
・計算力：数式組み立て（中）、数式計算（中）
・時間目安：2分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、二項分布の確率の比のテーマに取り組みます！
公式問題集の問題を例にして「A. 成功回数$${x}$$を確率変数とする確率$${P(X=x)}$$」と「B. 成功回数に１を加算した$${x+1}$$を確率変数とする確率$${P(X=x+1)}$$」の比を見ます。

公式問題集の解答が本当に２つの確率の比になっているかを可視化して確認いたします！

まずは二項分布のおさらいから。

二項分布

📕公式テキスト：2.7.2 二項分布（72ページ～）

サイコロを７回振って２以下の目が出る回数を二項分布で考えます。
・サイコロを７回振る試行・・・試行回数$${n=7}$$
・２以下の目が出る確率・・・成功確率$${p=1/3}$$
・２以下の目が出る回数・・・成功回数$${x}$$

このサイコロの試行を二項分布$${Bin(n,p)}$$の確率質量関数$${f(x)}$$に当てはめてみます。

サイコロの試行の確率は、
$${f(x) =\ _nC_x \ p^x \ (1-p)^{n-x}=\ _7C_x\ \left( \frac{1}{3}\right)^x\ \left(1-\frac{1}{3} \right)^{7-x}}$$
です。

成功回数$${x}$$に$${0, 1, \cdots, 7}$$を当てはめて、確率を計算しましょう。
確率は表の②確率（f(x)）の数値になりました（EXCELで計算しました）。

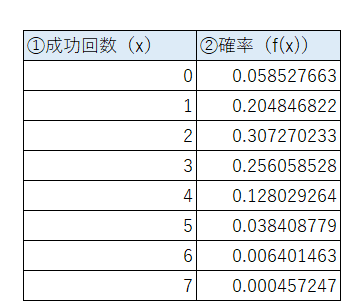
グラフを見ましょう。

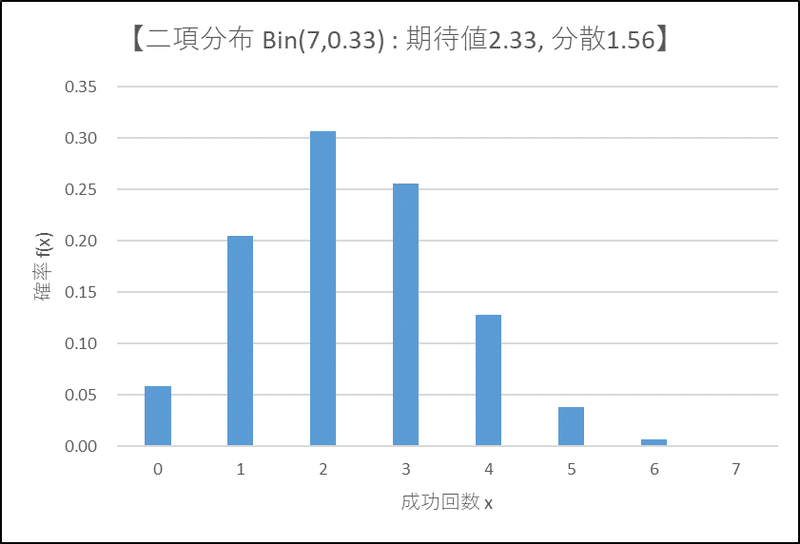
確率の峰（山のピーク）は成功回数２回のときです。
峰が左側に寄っていて、右側に裾が長いことを確認できました。
「A. 成功回数$${x}$$を確率変数とする確率$${P(X=x)}$$」の部分を見てまいりました。

二項分布の比

$${\boldsymbol{\cfrac{-x+7}{2x+2}}}$$を追え！

続いて「B. 成功回数に１を加算した$${x+1}$$を確率変数とする確率$${P(X=x+1)}$$」を見つつ、A. と B. の比を見てまいりましょう。

次の表の④が「B. 成功回数に１を加算した$${x+1}$$を確率変数とする確率$${P(X=x+1)}$$」です。

そして⑤がA. と B. の比（④÷②）、⑥が公式問題集の解答である$${\cfrac{-x+7}{2x+2}}$$の値です。

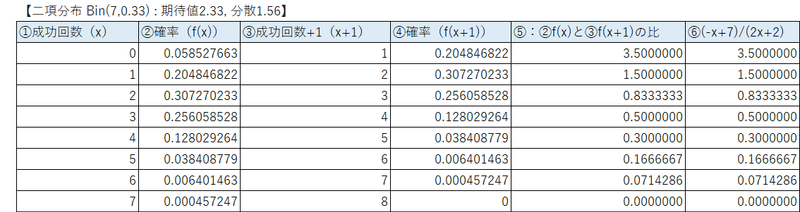
⑤と⑥は一致しています！
⑥$${\cfrac{-x+7}{2x+2}}$$が確率の比$${\cfrac{P(X=x+1)}{P(X=x)}}$$であることを、実際に確率の数値を追って確認することができました。

公式問題集の解答では「数式で確率の比」を導きました。
この「知る」では「実際に計算した確率の数値から確率の比」を確認しました。

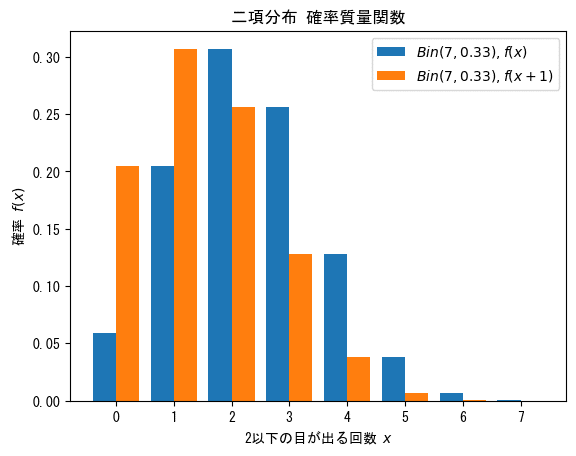
確率の比のグラフを可視化してみましょう。

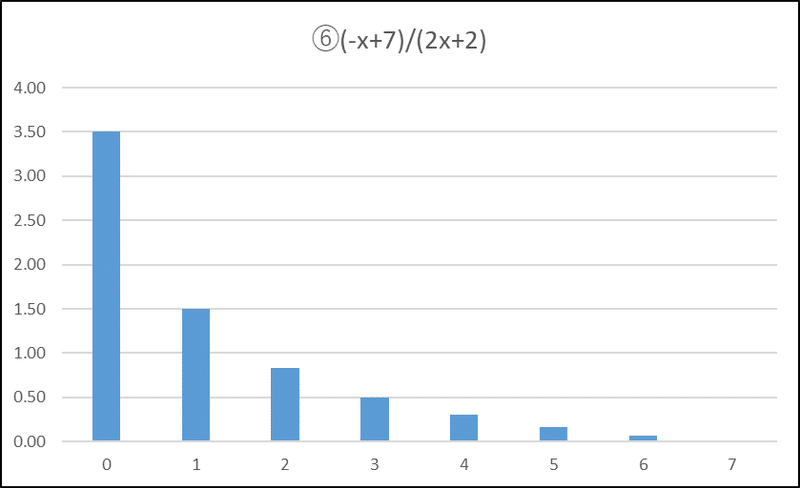
成功回数 1 回 vs 成功回数 0 回のときの比 3.5 をピークにして、減衰していることが分かります。

また、グラフの０回～１回の値は１以上です。
「成功回数１回ｖｓ成功回数０回」と「成功回数２回ｖｓ成功回数１回」のときの比は、$${P(X=x+1)}$$の方が確率が高いのです。
一方で、２回以上、つまり、「成功回数３回ｖｓ成功回数２回」のときは逆転して、$${P(X=x)}$$の方が確率が高いのです。
このことは、二項分布$${Bin(7, 1/3)}$$の確率の峰が成功回数２回のときであることを示唆しているのでしょう。

ここまでは、試行回数$${n=7}$$、成功確率$${p=1/3}$$のケースを確認してきました。

一般化した確率の比の式を追え！

次に、試行回数と成功確率を特定しない、一般化したケースを見てまいりましょう。

一般化した確率の比の式は「問題を解く」の計算式の中にあります。
$${\cfrac{P(X=x+1)}{P(X=x)}=\cfrac{(n-x)p}{(x+1)(1-p)}}$$です。

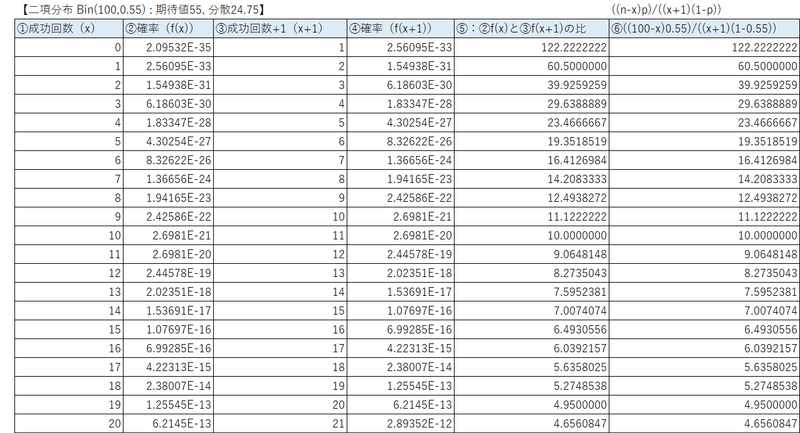
成功回数$${n=100}$$、成功確率$${p=0.55}$$の二項分布$${Bin(100,0.55)}$$を見てみましょう。
⑤の確率の比と⑥の$${\cfrac{(n-x)p}{(x+1)(1-p)}}$$は一致しています。

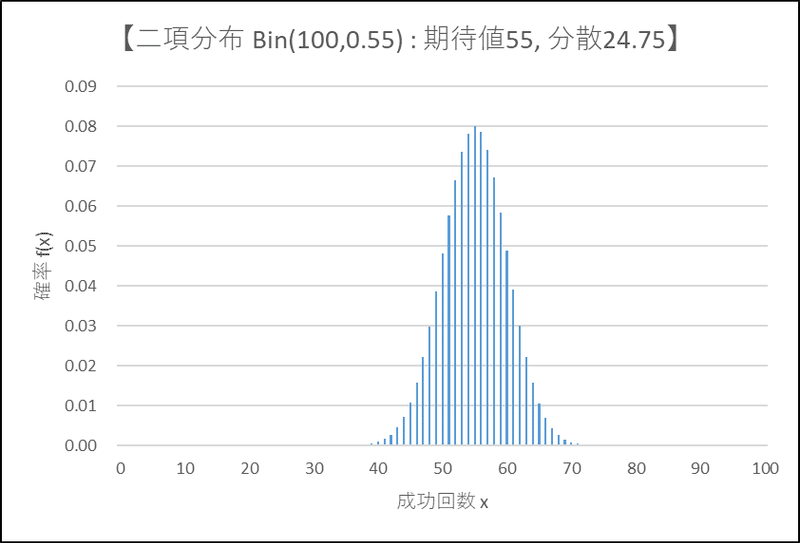
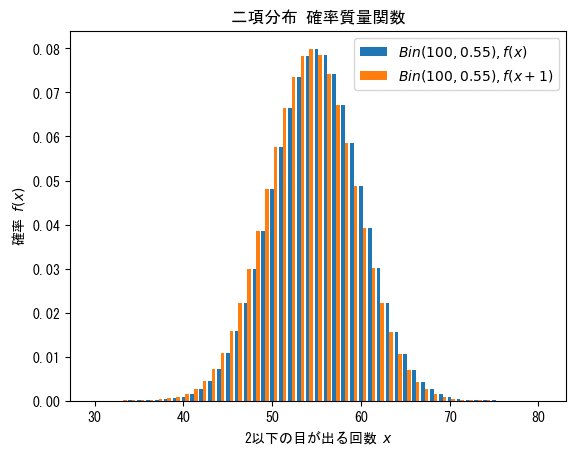
この二項分布のグラフは次のような形状になります。

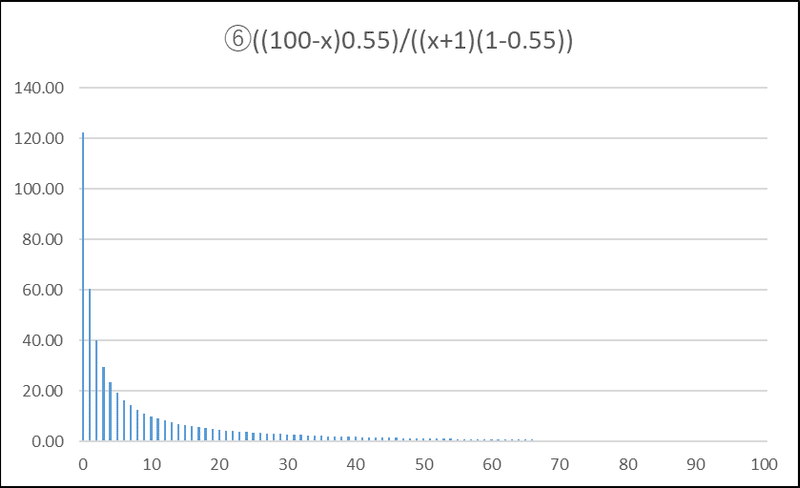
また、確率の比のグラフは次のとおりです。

確率変数$${x}$$と確率変数$${x+1}$$の確率の比を見てきました。
確率はいろんな角度から眺めることができるのだと、改めて実感いたした次第です。

実践する

二項分布の確率の比を計算してグラフを描画してみよう！

「知る」に掲載の確率表を計算したり、グラフに描いてみましょう！

電卓・手作業で作成してみよう！

「知る」の内容を参照しつつ、$${Bin(7,1/3)}$$の確率計算・比計算とグラフ描画を行ってみましょう。
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

二項分布の計算シート
EXCELサンプルファイルの顔ぶれを紹介いたします。
二項分布のパラメータ、試行回数$${n}$$と成功確率$${p}$$をさまざまな値に変えて、確率、確率の比、グラフの形状をご堪能ください！

【5-5_２項確率の比（BINOM.DIST関数）比率の一般化】シート
二項分布の確率の計算に「BINOM.DIST関数」を使用しています。

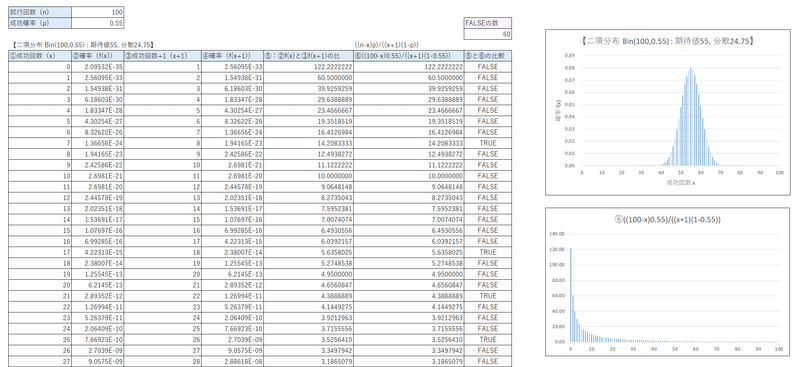
ちなみに、この関数の計算端数丸め処理の関係で、⑤と⑥が完全一致しない状況（見た目は合致しているけれども）が発生しています。
「FALSEの数」の数字が一致しない件数を示しています。

そこで検証目的で、$${f(x) =\ _nC_x \ p^x \ (1-p)^{n-x}}$$の確率式で計算したシートを作成してみました。

【5-5_２項確率の比（計算式）比率の一般化】シート

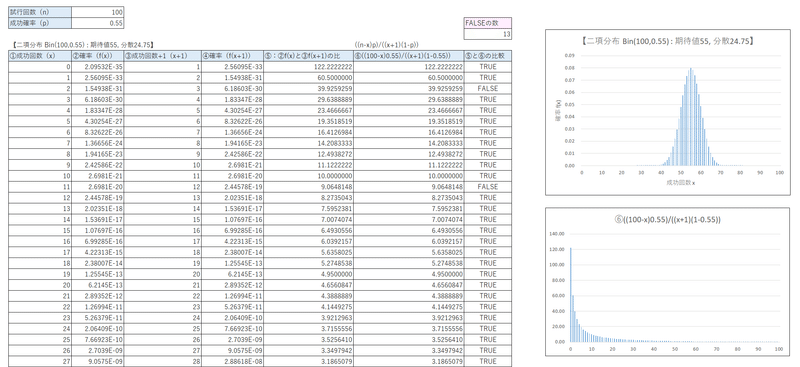
こちら計算にも完全一致しないケースがありました。

小数点以下の桁数が多い場合に微小な計算誤差が発生することを確認できました。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、二項分布の確率の比に取り組みます。
設定を変更して、さまざまな二項分布の確率の比をご確認ください！

①インポート
scipy.statsのbinomで二項分布の確率質量関数、累積分布関数を取得します。

import pandas as pd
import numpy as np
from scipy.stats import norm, binom
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②グラフ１：$${\boldsymbol{Bin(7,1/3)}}$$のケース 
試行回数が少ない場合に使用します。
試行回数n、成功確率pにさまざまな値を設定して、二項分布のグラフを確認してみてくださいね。
グラフの見え方が変だな、というときは、グラフの表示区間 x_min、x_maxで調整してください。

■設定

### 設定
# 【設定】二項分布のパラメータ 試行回数n, 成功確率p
n, p = 7, 1/3

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 0, 7

■確率表の作成（データフレーム）、棒グラフの作成

### 確率表の作成（データフレーム）、棒グラフの作成
# 確率変数と二項分布の確率の算出
x = np.arange(x_min, x_max+1)    # 確率変数 X の値を取得
y = binom.pmf(x, n=n, p=p)       # 二項分布Bin(n,p)_f(x)を算出
y2 = binom.pmf(x+1, n=n, p=p)    # 二項分布Bin(n,p)_f(x+1)を算出

# 二項分布の確率表の作成（データフレーム）
df_bin = pd.DataFrame({'2以下の目が出る回数': x, '確率f(x)': y, 
                       '確率f(x+1)': y2, '比': y2/y})
display(df_bin)

# 描画 binom.pmf(x, 試行回数, 成功確率)
plt.bar(x, y, label=f'$Bin({n},{p:.2f}), f(x)$', width=0.4)
plt.bar(x+0.4, y2, label=f'$Bin({n},{p:.2f}), f(x+1)$', width=0.4)
plt.title('二項分布 確率質量関数')
plt.xlabel('2以下の目が出る回数 $x$')
plt.ylabel('確率 $f(x)$')
plt.xticks(x+0.2, x)

plt.legend()

# plt.savefig('./binom_pmf1_bar.png') # グラフ画像ファイルの保存
plt.show()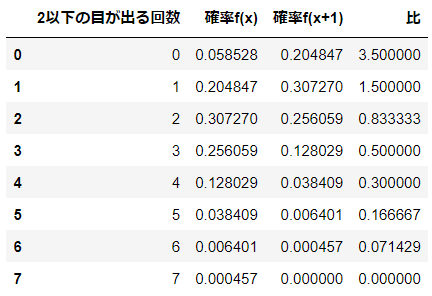

■折れ線グラフの作成

### 折れ線グラフの作成
# 描画 binom.pmf(x, 試行回数, 成功確率)
plt.plot(x, y, label=f'$Bin({n},{p:.2f}), f(x)$')
plt.plot(x+0.4, y2, label=f'$Bin({n},{p:.2f}), f(x+1)$')
plt.title('二項分布 確率質量関数')
plt.xlabel('2以下の目が出る回数 $x$')
plt.ylabel('確率 $f(x)$')

plt.legend()

# plt.savefig('./binom_pmf1_plot.png') # グラフ画像ファイルの保存
plt.show()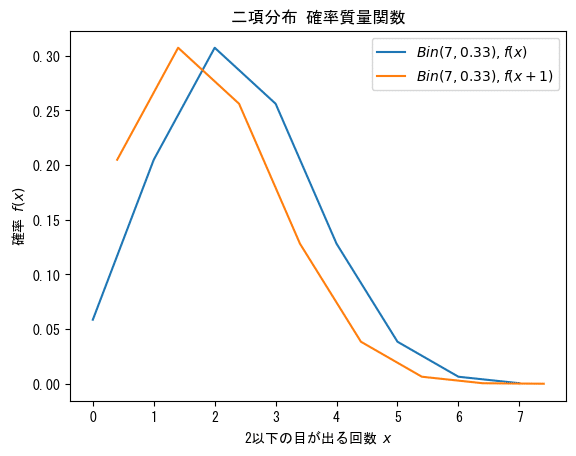

③グラフ２：$${\boldsymbol{Bin(100,0.55)}}$$のケース 
試行回数が多い場合に使用します。
確率表（データフレーム）の表示件数を少なくしています（df_bin.head()）。

■設定

### 設定
# 【設定】二項分布のパラメータ 試行回数n, 成功確率p
n, p = 100, 0.55

# 【設定】グラフの表示区間[x_min, x_max]
x_min, x_max = 30, 80

■確率表の作成（データフレーム）、棒グラフの作成

### 確率表の作成（データフレーム）、棒グラフの作成
# 確率変数と二項分布の確率の算出
x = np.arange(x_min, x_max+1)    # 確率変数 X の値を取得
y = binom.pmf(x, n=n, p=p)       # 二項分布Bin(n,p)_f(x)を算出
y2 = binom.pmf(x+1, n=n, p=p)    # 二項分布Bin(n,p)_f(x+1)を算出

# 二項分布の確率表の作成（データフレーム）
df_bin = pd.DataFrame({'2以下の目が出る回数': x, '確率f(x)': y, 
                       '確率f(x+1)': y2, '比': y2/y})
display(df_bin.head())

# 描画 binom.pmf(x, 試行回数, 成功確率)
plt.bar(x, y, label=f'$Bin({n},{p:.2f}), f(x)$', width=0.4)
plt.bar(x+0.4, y2, label=f'$Bin({n},{p:.2f}), f(x+1)$', width=0.4)
plt.title('二項分布 確率質量関数')
plt.xlabel('2以下の目が出る回数 $x$')
plt.ylabel('確率 $f(x)$')

plt.legend()

# plt.savefig('./binom_pmf2_bar.png') # グラフ画像ファイルの保存
plt.show()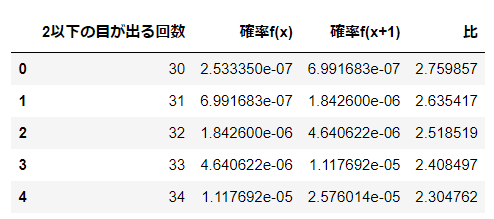

■折れ線グラフの作成

### 折れ線グラフの作成
# 描画 binom.pmf(x, 試行回数, 成功確率)
plt.plot(x, y, label=f'$Bin({n},{p:.2f}), f(x)$')
plt.plot(x+0.4, y2, label=f'$Bin({n},{p:.2f}), f(x+1)$')
plt.title('二項分布 確率質量関数')
plt.xlabel('2以下の目が出る回数 $x$')
plt.ylabel('確率 $f(x)$')

plt.legend()

# plt.savefig('./binom_pmf2_plot.png') # グラフ画像ファイルの保存
plt.show()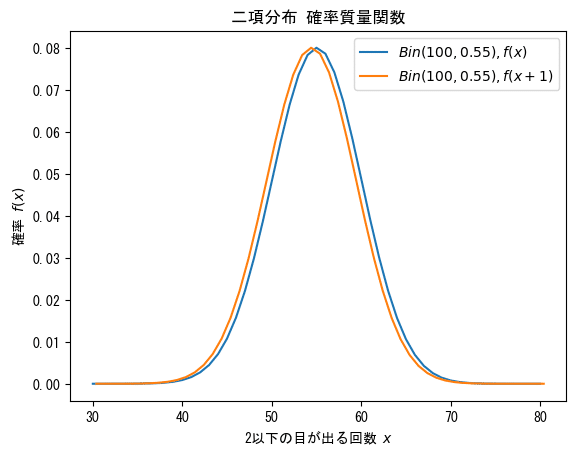

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

Open AIのGPT-4が猛威を振るっています！（執筆時点のトピックス）
しばらくは実験のお祭りで界隈は賑わうことでしょう。
AIが進化して暮らしが豊かになることを願ってやみません。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次