第４章「距離に基づいた異常検知」

書籍の著者　笛田薫 先生、江崎剛史 先生、李鍾賛 先生

この記事は、テキスト「Pythonではじめる異常検知入門」の第４章「距離に基づいた異常検知」の通称「寄り道写経」を取り扱います。

テキストは第４章のPythonコードを掲載していないので、寄り道写経は勝手気まま度マックスなのです！
ではテキストを開いて異常検知の旅に出発です🚀

このシリーズは書籍「Pythonではじめる異常検知入門」（科学情報出版、「テキスト」と呼びます）の異常検知の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。

はじめに

テキスト「Pythonではじめる異常検知入門」のご紹介

テキストは、2023年4月に発売された異常検知の入門書です。
数式展開あり、Python実装ありのテキストなのです。
Jupyter Notebook 形式のソースコードと csv 形式のデータは、書籍購入者限定特典として書籍掲載のURLからダウンロードできます。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonではじめる異常検知入門－基礎から実践まで－」初版、著者 笛田薫／江崎剛史／李鍾賛、オーム社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

第４章 距離に基づいた異常検知

Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。

テキストのこの章は主に距離に基づいた異常検知のベース知識の習得に特化しています。
具体的には「マハラノビス距離」「ユークリッド距離」「ミンコフスキー距離」「マンハッタ距離」「Jacobの類似性」「ジャッカード類似性」「余弦類似度（コサイン類似度）」「最近傍からの距離」「$${k}$$近傍からの平均距離」「$${k}$$最近傍までの距離の中央値」の計算式や計算結果を掲載しています。
そしてPythonコードの提供はありません！

この記事は以下の２点の寄り道写経に取り組みます。
真っ白なキャンバスに向かっている感じです！

インポート

### インポート

# 数値・確率計算
import numpy as np

# 距離・類似度
from scipy.spatial import distance
from sklearn.metrics import jaccard_score
from sklearn.metrics.pairwise import cosine_similarity

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

Google Colab をご利用の場合は「描画」箇所を以下のように差し替えてください。

!pip install japanize_matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

4-2 類似度（距離）

さあ、類似度・距離を計算しまくります！！！

■ マハラノビス距離
テキストのマハラノビス距離の数式を引用します。
２つのデータ点ベクトル$${\boldsymbol{p}}$$, $${\boldsymbol{q}}$$の距離を計算するものです。

$${\boldsymbol{S}}$$は分散共分散行列、$${\boldsymbol{S}^{-1}}$$は分散共分散行列の逆行列です。

２次元の正規分布乱数データを作成して、マハラノビス距離を算出してみます。
ではデータを作成しましょう。

### 100行2列のデータを作成

# 乱数生成器の設定
rng = np.random.default_rng(seed=777)

# 平均、分散共分散行列の設定
mean_true = [3, 5]  # 平均
sigma1 = 1.5        # 標準偏差1
sigma2 = 1          # 標準偏差2
rho = 0.8           # 相関係数
cov_true = np.array([[sigma1**2, sigma1*sigma2*rho],
                     [sigma1*sigma2*rho, sigma2**2]])
print('--- 作成パラメータ ---')
print('平均:')
print(mean_true)
print('標準偏差:')
print([sigma1, sigma2])
print('分散共分散行列:')
print(cov_true)

# データの作成（２変量正規分布の乱数）
data = rng.multivariate_normal(mean=mean_true, cov=cov_true, size=200)
print('\n--- 作成データの概要 ---')
print('data.shape: ', data.shape)

# データの平均・標準偏差・分散共分散行列を算出
mean_data = data.mean(axis=0)
std_data =  data.std(ddof=0, axis=0)
cov_data = np.cov(data.T, ddof=0)
print('平均:')
print(mean_data)
print('標準偏差:')
print(std_data)
print('分散共分散行列:')
print(cov_data)

【実行結果】
(200, 2)の形状のデータが出来ました。

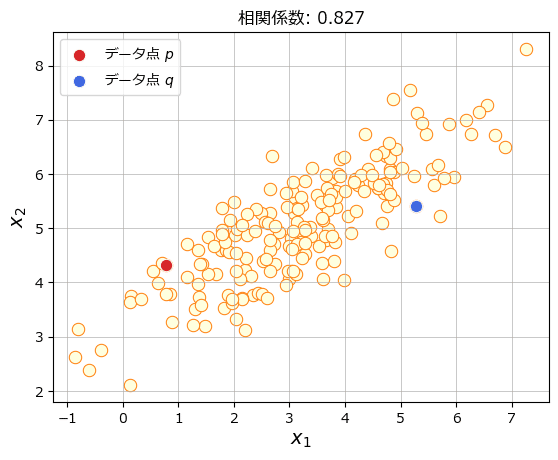
データを散布図で可視化しましょう。
「距離を算出する２つのデータ点の設定」で指定した２つの index のデータ点の距離を算出します。

### データの可視化

# 距離を算出する２つのデータ点の設定
p_idx = 50
q_idx = 1

# 全データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], s=80, color='lightyellow',
                ec='tab:orange')

# データ点p(index=0)の描画
sns.scatterplot(x=[data[p_idx, 0]], y=[data[p_idx, 1]], s=80, color='tab:red',
                label='データ点 $p$')

# データ点q(index=1)の描画
sns.scatterplot(x=[data[q_idx, 0]], y=[data[q_idx, 1]], s=80, color='royalblue',
                label='データ点 $q$')

# 修飾
plt.title(f'相関係数: {np.corrcoef(data.T)[0, 1]:.3f}')
plt.xlabel('$x_1$', fontsize=14)
plt.ylabel('$x_2$', fontsize=14)
plt.grid(lw=0.5)

【実行結果】
強い正の相関のデータです。
赤と青のデータの距離を計算します。

ではでは、マハラノビス距離を算出します。
上述の数式とscipyの関数で計算します。
なお、計算参考事例を見つけられなかったので、計算ロジックの正確性は何とも言えません・・・。

### マハラノビス距離の算出

# マハラノビス距離を算出する２つのデータ点を取得
p = data[p_idx, :]
q = data[q_idx, :]
print('データ点 p:', p)
print('データ点 q:', q)

# データの分散共分散行列の逆行列を算出
cov_inv_data = np.linalg.pinv(cov_data)

# マハラノビス距離の算出：公式利用
mahal_calc = np.sqrt((p - q) @ cov_inv_data @ (p - q).reshape(-1, 1))[0]
print('\n--- マハラノビス距離 ---')
print('数式利用 : ', mahal_calc)

# マハラノビス距離の算出：scipy利用
mahal_scipy = distance.mahalanobis(u=p, v=q, VI=cov_inv_data)
print('scipy利用: ', mahal_scipy)

【実行結果】

【耳より情報👂️】
第５章以降の主役「ホテリングの$${T^2}$$法」とマハラノビス距離の関係性です。
ホテリングの$${T^2}$$法の異常度に用いる「$${a(x^{\prime})}$$」はマハラノビス距離の二乗です。
マハラノビス距離の平方根を外すと異常度$${a(x^{\prime})}$$になるのです。
ただ、この際に用いるマハラノビス距離の数式は、上述の数式と若干異なります。

あるデータ点$${\boldsymbol{x}}$$（ベクトル）とデータ群の平均$${\boldsymbol{\mu}}$$（ベクトル）間の距離を示しているようです。
「マハラノビス距離」で検索すると、大半のWebサイトがこの数式を掲載している印象です。

◆ ◆ ◆ ◆ ◆

■ Jacobの類似性
テキストの Jacob の類似性の数式を引用します。
２つのデータセット$${A,B}$$に共通するデータ点の個数で距離を計算するようです。

集合の和集合$${\cup}$$と積集合$${\cap}$$の記号が出てきました！

Jacobの類似性を計算してみましょう。
Pythonで集合といえば集合型「set」です。
set を用いてデータセット$${A,B}$$を表現します。
最終行の「len(A & B) / len(A | B)」では、「&」で積集合$${\cap}$$、「|」で和集合$${\cup}$$を計算しています。

## Jacobの類似性の計算例

# 集合A, Bの設定
A = set([0, 1, 4])
B = set([1, 3, 4, 5, 6, 7, 8])
print('--- 作成データの概要 ---')
print(f'集合A: {A}\n集合B: {B}')

# 計算
print('\n--- 計算過程 ---')
print(f'A ∩ B   要素数: {len(A & B)},  要素: {A & B}')
print(f'A ∪ B  要素数: {len(A | B)},  要素: {A | B}, ')
print('\n--- 計算結果 ---')
print(f'Jacobの類似性: {len(A & B) / len(A | B)}')

【実行結果】
Jacobの類似性は$${0.25}$$です。

◆ ◆ ◆ ◆ ◆

■ ジャッカード類似性
テキストのジャッカード距離の数式を引用します。
２つのデータ点ベクトル$${\boldsymbol{p}}$$, $${\boldsymbol{q}}$$のすべての変数が二値であり、共通する変数の個数で距離を計算するようです。

右辺の変数の内容です。
・$${m_{01}}$$：$${p_i=0}$$かつ$${q_i=1}$$の個数
・$${m_{10}}$$：$${p_i=1}$$かつ$${q_i=0}$$の個数
・$${m_{11}}$$：$${p_i=1}$$かつ$${q_i=1}$$の個数

テキストの数値例をお借りしてPythonコードを描きます。

### テキストの数値例

# p,qの設定 テキストの値を引用
p = np.array([1, 1, 0, 0, 1, 0])
q = np.array([1, 0, 1, 0, 0, 1])
print('--- データの概要 ---')
print('データ点 p:', p)
print('データ点 q:', q)

# m01, m10, m11の算出
m01 = sum((p == 0) & (q == 1))
m10 = sum((p == 1) & (q == 0))
m11 = sum((p == 1) & (q == 1))

# Jaccard類似性の算出
J_pq = m11 / sum([m01, m10, m11]) 

# 結果表示
print('\n--- 計算過程と結果 ---')
print(f'm01={m01}, m10={m10}, m11={m11}, m01+m10+m11={m01+m10+m11}')
print(f'Jaccard類似性={J_pq}')

【実行結果】
ジャッカード類似性は$${0.2}$$です。

【scikit-learn コーナー📯】
例題データのジャッカード距離を scikit-learn の jaccard_score() で計算します。
評価指標ライブラリを用いるので、２つのデータを与える引数は y_true と y_pred になっています。

# ジャッカードスコアの計算
j_score = jaccard_score(y_true=p, y_pred=q, average='binary')
print('ジャッカードスコア:', j_score)

【実行結果】
サクッと計算できました。

◆ ◆ ◆ ◆ ◆

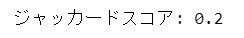
■ 余弦類似度（コサイン類似度）
テキストのコサイン類似度の数式を引用します。
２つのデータ点ベクトル$${\boldsymbol{p}}$$, $${\boldsymbol{q}}$$間の距離を計算します。

ジャッカード距離のデータを用いて、３つの方法でコサイン類似度を算出します。

① テキストの数式

sum(p * q) / np.sqrt(sum(p**2) * sum(q**2))

【実行結果】
コサイン類似度は$${0.3 \cdots}$$です。

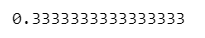
② 行列計算
次の数式を用いてコサイン類似度を計算します。

# 行列計算
p @ q / (np.linalg.norm(p) * np.linalg.norm(p))

【実行結果】
微妙に異なります（汗）

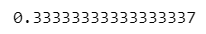
こちらの計算式のほうがいい感じでした。

# 行列計算
p @ q / np.sqrt((p @ p) * (q @ q))

【実行結果】

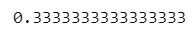
③ scikit-learn の cosine_similarity() 利用
pとqの形状を reshape にて (1, 6) の２次元に変換して引数に与えます。

# scikit-learnで余弦類似度（コサイン類似度）を計算
cosine_similarity(X=p.reshape(1, -1), Y=q.reshape(1, -1))[0][0]

【実行結果】
末尾の値が・・・（うっ）

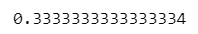
お試しコードの寄り道、楽しかったですね！✨

4-3 距離に基づく異常検知のアプローチ

テキストの例4-3-1 ～ 4-3-5の例題を寄り道写経します！
１次元データについて４つの距離を用いて異常度を算出、異常度判定をします。
そして１次元の数直線を用いて異常判定されたデータを点を描画します。

例 4-3-1 全てのデータ点と最も離れているデータ点を異常と判断
他のデータ点との距離の合計値が最も大きいデータ点を異常と判断します。
テキストのデータを引用して、各データ点の異常度を算出し、異常度が最大のデータ点を異常検知します。
コードの「[sum(abs(D - i)) for i in D]」で異常度を計算しています。

### 例4-3-1

# データの登録 ※テキストのデータを引用
D = np.array([1, 2, 3, 8, 20, 21])
print('データセット','\t:',  D)

# 異常度αの算出（データ点間のマンハッタン距離の合計値）
alpha = np.array([sum(abs(D - i)) for i in D])
print('異常度α', '\t:', alpha)

# 異常度が最大の要素の表示
max_idx = alpha.argmax()
print('異常値が最大のデータ点:', D[max_idx], ', 異常度:', alpha[max_idx])

【実行結果】
データ点$${21}$$が異常と判定されました。

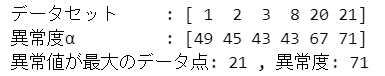
可視化しましょう。
テキスト図4-1に相当します。

### 図4-1

## 描画用の設定
# 最大値の点の色・マーカーを変えるためのhueの設定 
hue = np.zeros(len(D))
hue[max_idx] = 1 

## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 0.4))
# 数直線（矢印線）の描画
plt.quiver(0, 0, 24, 0, angles='xy', scale_units='xy', scale=1, width=0.005)
# 数直線上にデータ点を描画
sns.scatterplot(x=D, y=np.zeros(len(D)), hue=hue, palette=['tab:blue', 'tab:red'],
                style=hue, markers=['o', 's'], s=100, legend=False)
# 修飾：x軸の範囲と目盛り
plt.xlim(-1, 24)
plt.xticks(range(0, 23))
# 修飾：枠線の消去
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
# 修飾：y軸の軸目盛りと軸ラベルの消去
plt.tick_params(left=False, labelleft=False);

【実行結果】
赤い四角点が異常と判定されたデータ点$${21}$$です。

◆ ◆ ◆ ◆ ◆

例 4-3-2 最近傍までの距離が最も大きいデータ点を異常と判断
最も近い他のデータ点との距離が最も大きいデータ点を異常と判断します。テキストのデータを引用して、各データ点の異常度を算出し、異常度が最大のデータ点を異常検知します。
コードの「[min(abs(D[D != i] - i)) for i in D]」で異常度を計算しています。

### 例4-3-2

# データの登録 ※テキストのデータを引用
D = np.array([1, 2, 3, 8, 20, 21])
print('データセット','\t:',  D)

# 異常度αの算出（最近傍からの距離）
alpha = np.array([min(abs(D[D != i] - i)) for i in D])
print('異常度α', '\t:', alpha)

# 異常度が最大の要素の表示
max_idx = alpha.argmax()
print('異常値が最大のデータ点:', D[max_idx], ', 異常度:', alpha[max_idx])

【実行結果】
データ点$${8}$$が異常と判定されました。

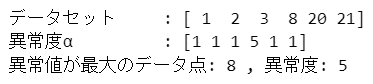
可視化しましょう。

### 例4-3-2 描画

## 描画用の設定
# 最大値の点の色・マーカーを変えるためのhueの設定 
hue = np.zeros(len(D))
hue[max_idx] = 1 

## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 0.4))
# 数直線（矢印線）の描画
plt.quiver(0, 0, 24, 0, angles='xy', scale_units='xy', scale=1, width=0.005)
# 数直線上にデータ点を描画
sns.scatterplot(x=D, y=np.zeros(len(D)), hue=hue, palette=['tab:blue', 'tab:red'],
                style=hue, markers=['o', 's'], s=100, legend=False)
# 修飾：x軸の範囲と目盛り
plt.xlim(-1, 24)
plt.xticks(range(0, 23))
# 修飾：枠線の消去
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
# 修飾：y軸の軸目盛りと軸ラベルの消去
plt.tick_params(left=False, labelleft=False);

【実行結果】
赤い四角点が異常と判定されたデータ点$${8}$$です。
確かにお隣さんとの距離が一番長いです！

◆ ◆ ◆ ◆ ◆

例 4-3-3 最近傍までの距離が最も大きいデータ点を異常と判断 その２
例4-3-2と同じ異常度判定の方法をデータセットを変更して実行します。

### 例4-3-3

# データの登録 ※テキストのデータを引用
D = np.array([1, 3, 5, 7, 100, 101, 200, 202, 205, 208, 210, 212, 214])
print('データセット','\t:',  D)

# 異常度αの算出（最近傍からの距離）
alpha = np.array([min(abs(D[D != i] - i)) for i in D])
print('異常度α', '\t:', alpha)

# 異常度が最大の要素の表示
max_idx = alpha.argmax()
print('異常値が最大のデータ点:', D[max_idx], ', 異常度:', alpha[max_idx])

【実行結果】
データ点$${205}$$が異常と判定されました。

可視化しましょう。
テキスト図4-2に相当します。

### 図4-2 ★テキストに無いコード

## 描画用の設定
# 最大値の点の色・マーカーを変えるためのhueの設定 
hue = np.zeros(len(D))
hue[max_idx] = 1 

## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 0.4))
# 数直線（矢印線）の描画
plt.quiver(-20, 0, 260, 0, angles='xy', scale_units='xy', scale=1, width=0.002)
# 数直線上にデータ点を描画
sns.scatterplot(x=D, y=np.zeros(len(D)), hue=hue, palette=['tab:blue', 'tab:red'],
                style=hue, markers=['o', 's'], s=20, legend=False)
# 修飾：x軸の範囲と目盛り
plt.xlim(-20, 260)
plt.xticks(range(0, 240, 20))
# 修飾：枠線の消去
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
# 修飾：y軸の軸目盛りと軸ラベルの消去
plt.tick_params(left=False, labelleft=False);

【実行結果】
赤い四角点が異常と判定されたデータ点$${205}$$です。

◆ ◆ ◆ ◆ ◆

例 4-3-4 $${\boldsymbol{k}}$$近傍点からの合計距離が最も大きいデータ点を異常と判断
最近傍点を$${k}$$個定めて、$${k}$$個の最近傍点からの合計距離が最も大きいデータ点を異常と判断します。
テキストのデータを引用して、$${k=3}$$のときの各データ点の異常度を算出し、異常度が最大のデータ点を異常検知します。
コードの「[np.sort(abs(D[D != i] - i))[:k].sum() for i in D]」で異常度を計算しています。

### 例4-3-4

# パラメータk
k = 3 

# データの登録 ※テキストのデータを引用
D = np.array([1, 3, 5, 7, 100, 101, 200, 202, 205, 208, 210, 212, 214])
print('データセット','\t:',  D)

# 異常度αの算出（k近傍からの距離の合計値）
alpha = np.array([np.sort(abs(D[D != i] - i))[:k].sum() for i in D])
print('異常度α', '\t:', alpha)

# 異常度が最大の要素の表示
max_idx = alpha.argmax()
print('異常値が最大のデータ点:', D[max_idx], ', 異常度:', alpha[max_idx])

【実行結果】
データ点$${101}$$が異常と判定されました。

可視化しましょう。
テキスト図4-3に相当します。

### 図4-3

## 描画用の設定
# 最大値の点の色・マーカーを変えるためのhueの設定 
hue = np.zeros(len(D))
hue[max_idx] = 1 

## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 0.4))
# 数直線（矢印線）の描画
plt.quiver(-20, 0, 260, 0, angles='xy', scale_units='xy', scale=1, width=0.002)
# 数直線上にデータ点を描画
sns.scatterplot(x=D, y=np.zeros(len(D)), hue=hue, palette=['tab:blue', 'tab:red'],
                style=hue, markers=['o', 's'], s=20, legend=False)
# 修飾：x軸の範囲と目盛り
plt.xlim(-20, 260)
plt.xticks(range(0, 240, 20))
# 修飾：枠線の消去
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
# 修飾：y軸の軸目盛りと軸ラベルの消去
plt.tick_params(left=False, labelleft=False);

【実行結果】
赤い四角点が異常と判定されたデータ点$${101}$$です。

$${k=4}$$の場合を試してみます。

### 例4-3-4

# パラメータk
k = 4

# データの登録 ※テキストのデータを引用
D = np.array([1, 3, 5, 7, 100, 101, 200, 202, 205, 208, 210, 212, 214])
print('データセット','\t:',  D)

# 異常度αの算出（k近傍からの距離の合計値）
alpha = np.array([np.sort(abs(D[D != i] - i))[:k].sum() for i in D])
print('異常度α', '\t:', alpha)

# 異常度が最大の要素の表示
max_idx = alpha.argmax()
print('異常値が最大のデータ点:', D[max_idx], ', 異常度:', alpha[max_idx])

【実行結果】
$${k=4}$$のときもデータ点$${101}$$が異常と判定されました。

念の為、描画します。

### 例4-3-4 k=4 の描画

## 描画用の設定
# 最大値の点の色・マーカーを変えるためのhueの設定 
hue = np.zeros(len(D))
hue[max_idx] = 1 

## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 0.4))
# 数直線（矢印線）の描画
plt.quiver(-20, 0, 260, 0, angles='xy', scale_units='xy', scale=1, width=0.002)
# 数直線上にデータ点を描画
sns.scatterplot(x=D, y=np.zeros(len(D)), hue=hue, palette=['tab:blue', 'tab:red'],
                style=hue, markers=['o', 's'], s=20, legend=False)
# 修飾：x軸の範囲と目盛り
plt.xlim(-20, 260)
plt.xticks(range(0, 240, 20))
# 修飾：枠線の消去
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
# 修飾：y軸の軸目盛りと軸ラベルの消去
plt.tick_params(left=False, labelleft=False);

【実行結果】

◆ ◆ ◆ ◆ ◆

例 4-3-5 $${\boldsymbol{k}}$$近傍点からの距離の中央値が最も大きいデータ点を異常と判断
最近傍点を$${k}$$個定めて、$${k}$$個の最近傍点からの距離の中央値が最も大きいデータ点を異常と判断します。
テキストのデータを引用して、$${k=3}$$のときの各データ点の異常度を算出し、異常度が最大のデータ点を異常検知します。
コードの「[np.median(np.sort(abs(D[D != i] - i))[:k]) for i in D]」で異常度を計算しています。

### 例4-3-5

# パラメータk
k = 3

# データの登録 ※テキストのデータを引用
D = np.array([1, 3, 5, 7, 100, 101, 200, 202, 205, 208, 210, 212, 214])
print('データセット','\t:',  D)

# 異常度αの算出（k近傍からの距離の合計値）
alpha = np.array([np.median(np.sort(abs(D[D != i] - i))[:k]) for i in D])
print('異常度α', '\t:', alpha)

# 異常度が最大の要素の表示
max_idx = alpha.argmax()
print('異常値が最大のデータ点:', D[max_idx], ', 異常度:', alpha[max_idx])

【実行結果】
データ点$${101}$$が異常と判定されました。

可視化しましょう。

### 例4-3-5 の描画

## 描画用の設定
# 最大値の点の色・マーカーを変えるためのhueの設定 
hue = np.zeros(len(D))
hue[max_idx] = 1 

## 描画処理
# 描画領域の指定
plt.figure(figsize=(7, 0.4))
# 数直線（矢印線）の描画
plt.quiver(-20, 0, 260, 0, angles='xy', scale_units='xy', scale=1, width=0.002)
# 数直線上にデータ点を描画
sns.scatterplot(x=D, y=np.zeros(len(D)), hue=hue, palette=['tab:blue', 'tab:red'],
                style=hue, markers=['o', 's'], s=20, legend=False)
# 修飾：x軸の範囲と目盛り
plt.xlim(-20, 260)
plt.xticks(range(0, 240, 20))
# 修飾：枠線の消去
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['bottom'].set_visible(False)
# 修飾：y軸の軸目盛りと軸ラベルの消去
plt.tick_params(left=False, labelleft=False);

【実行結果】
赤い四角点が異常と判定されたデータ点$${101}$$です。

数直線の描画が楽しかったです！

第４章の寄り道写経は以上です。

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。