mendelian randomization
methods for causal inference using genetic variants chapter 4の勉強まとめ

Mendelian Randomizationを”MR”と略します。
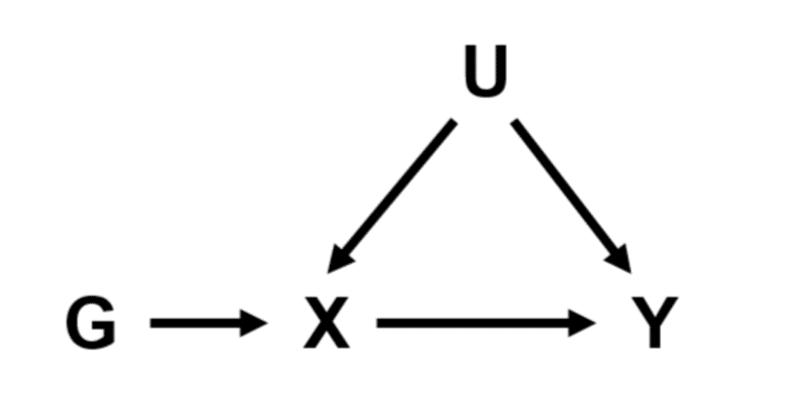
Y: アウトカム, Outcome
X: 要因 (暴露), Exposure
U: 交絡因子, Confounder (often unmeasured)
G: 操作変数, 遺伝的バリアント Genetic variant as an instrumental variable
とおきます。

IVW (Inverse-variance weighted)法

操作変数の妥当性を満たす遺伝的バリアントがJ個あるとする。
また、暴露とアウトカムの関係が線形で効果修飾がないと仮定する。

$$
E(X|G_j=g, U=u) = \beta_{X0j} + \beta_{Xj} g + \beta_{XU} u\\
E(Y|G_j=g, U=u) = \beta_{Y0j} + \beta_{Yj} g + \beta_{YU} u\enspace for\: j=1, 2, …, J\\
E(Y|do(X=x), U=u) =\theta_0 + \theta_x + \beta_U u\\
causal\:effect\:parameter\:\theta=\frac{\beta_{Yj}}{\beta_{Xj}} \enspace for\:all\:j=1, 2, …, J
$$

j番目の遺伝的バリアントにおける推定値は

$$
\hat\theta_j=\frac{\hat\beta_{Yj}}{\hat\beta_{Xj}}
$$

標準誤差は

$$
se(\hat\theta_j) = |\frac{se(\hat\beta_{Yj})}{\hat\beta_{Xj}}|
$$

第一項のみを用いているが、GWASデータではGとXの不確実性に比べてGとYの不確実性が大きい場合が多い。
また、最初の式はUの項を含んでいるが、操作変数が妥当であればUとGは独立しているため、Uを調整しなくても結果は同じになる。

複数のバリアントをまとめる場合はどちらが"effect allele"でどちらが"reference allele"であるかを統一しておかねばならない。

IVW meta-analysis

summarized dataでJ個の推定値 $${\theta_1, \theta_2, …, \theta_J}$$ を統合するには？

IVW法の式

$$
\hat\theta_{IVW} = \frac{\sum_j \hat\theta_j se(\hat\theta_j)^{-2}}{\sum_j se(\hat\theta_j)^{-2}}\\
=\frac{\sum_j \hat\beta_{Yj} \hat\beta_{Xj} se(\hat\beta_{Yj})^{-2}}{\sum_j \hat\beta_{Xj}^2 se(\hat\beta_{Yj})^{-2}}
$$

バリアント毎の推定値の重みづけ平均を表す。

IVW推定値の標準誤差は (fixed-effectとして)

$$
se(\hat\theta_{IVW}) =\sqrt{1 \over\sum_j \hat\beta_{Xj}^2 se(\hat\beta_{Yj})^{-2}}
$$

一見複雑にみえるが、足し算、二乗、平方根の組み合わせであり、（解析ソフトを使用せずとも）電卓でも計算できるレベルであるとのこと！！

難しく見えていたMendelian Randomizationも、実際にやっていることは単純であることがわかった

問題はSNPに詳しくなりどのSNPが曝露と関連しているか、ほか、操作変数の妥当性を満たすかをいかに議論するかだろう