mendelian randomization
methods for causal inference using genetic variants chapter 8の勉強まとめ

＊Mendelian Randomizationを”MR”と略します。

Weak instrument bias

弱い操作変数とは
・暴露との関連が統計的に弱い操作変数
・操作変数が弱くても、操作変数の仮定を満たせば妥当な操作変数である。
・サンプルサイズが∞であればバイアスはゼロに近づく。
・しかし、サンプルサイズが有限であれば、バイアスを生じうる。

弱い操作変数の説明

説明を単純にするため、操作変数は 0 or 1の二値のみをとり、交絡因子は一つとする。
操作変数とアウトカムの関連は、①操作変数が暴露と関連することによる効果　と②操作変数が交絡因子とランダムに関連する影響 の要素があるとする。
＊交絡因子以外の偶然の影響（chance)で操作変数とアウトカムが関連することもあるが、この影響は無視できるとする。

操作変数が「強い」場合、操作変数と暴露の関連が強いため②の影響は小さい。しかし、操作変数が「弱い」場合、②の操作変数と交絡因子の関連の影響が無視できなくなってくる。このことを数学的に表現することができる。

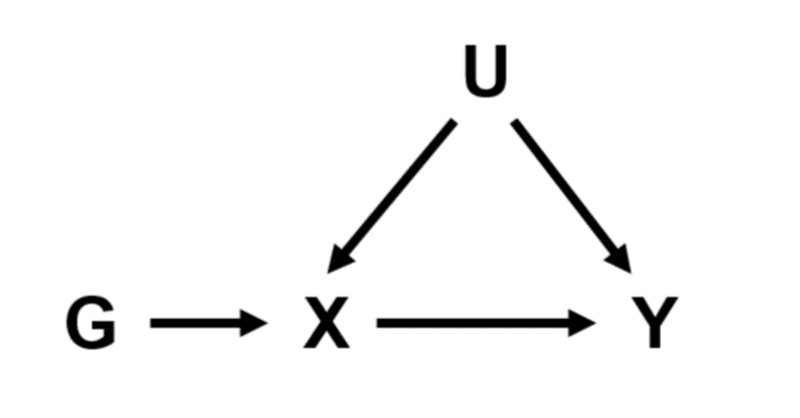
Y: アウトカム, Outcome
X: 要因 (暴露), Exposure
U: 交絡因子, Confounder (often unmeasured)
G: 操作変数, 遺伝的バリアント Genetic variant as an instrumental variable
とおく。

線形の関係である仮定のもとで、

$$
X= \alpha_0 + \alpha_1 G + \alpha_2 U + \epsilon_X\\
Y =\theta_0 + \theta_1 X + \theta_2 U +\epsilon_Y
$$

と表現できる。

2つの遺伝的バリアントのサブグループ間の暴露の差は
$${ \vartriangle X =\alpha_1+\alpha_2\vartriangle U+ \vartriangle \epsilon_X }$$であり、
アウトカムの差は
$${ \vartriangle Y =\theta_1+\theta_2\vartriangle U+ \vartriangle \epsilon_Y }$$と書ける。
$${\vartriangle\epsilon_X}$$と$${\vartriangle\epsilon_Y}$$がゼロであれば、ratio methodによる操作変数の効果推定は

$$
\frac {\vartriangle Y}{\vartriangle X} = \frac {\theta_1 \vartriangle X + \theta_2 \vartriangle U } { \vartriangle X} = \theta_1 + \frac {\theta_2 \vartriangle U}{\alpha_1 + \alpha_2 \vartriangle U}
$$

である。
ΔUがゼロであれば、第二項は消去されて推定値は$${\theta_1}$$となり、暴露がアウトカムに与える真の因果効果が推定できる。

もし$${\alpha_1}$$ （バリアント暴露に与える影響）が $${\theta_2\vartriangle U}$$に比べて大きければ、第二項はゼロに近づくため、推定値はやはり$${\theta_1}$$に近似できる＝強い操作変数のとき

しかし、$${\alpha_1}$$がゼロに近づく（＝弱い操作変数の）とき、推定値は

$$
\frac {\vartriangle Y}{\vartriangle X} = \theta_1 + \frac {\theta_2}{\alpha_1}
$$

に近づく。ここで第二項は交絡因子がアウトカム、暴露に与える影響から計算される。

すなわち、操作変数が弱いときには、操作変数と交絡因子の関連がアウトカム・暴露に与える影響がバイアスとなりうる。＝観察研究で得られるみかけの関連に近づく方向のバイアスが生じる。

また、Two-sample MRにおいてはsample oneのΔＵとsample twoのΔＵが異なる場合があり、第二項で打消しあわないかもしれない。

ほかにも、measurement errorの観点を用いた説明や、図を用いた視覚的な説明が教科書に記載されているが、割愛する。

弱い操作変数による因果効果の推定

one-sample MRにおいて、弱い操作変数のバイアスは観察された暴露とアウトカムの関連の方向に近づく。
バイアスの大きさは操作変数に対する暴露の回帰のF 統計量の期待値に基づく。
2SLS法によるバイアスは 1/E(F)に近似できる。ここで、E(F)はF統計量の期待値とする。この近似式は操作変数が少なくとも3つ以上ないと妥当ではない。

F統計量は遺伝的バリアントが説明する暴露の分散 ($${R^2}$$)、サンプルサイズ(N)、操作変数の数 (K)によって決定される。

$$
F=(\frac{N-K-1}{K})(\frac{R^2}{1-R^2})
$$

バリアントが一つのとき

$$
F\:statistic =\Big(\frac{\hat\beta_X}{se(\hat\beta_X)}\Big)^2
$$

biallelic SNPのとき、$${R^2}$$は下式で近似できる。
MAF=Minor Allele Frequency

$$
R^2=2\beta_x^2 MAF (1-MAF)
$$

例題) あるbiallelic SNPにおいて一つのalleleが変化する毎に暴露が0.15SD増加し、Minor Allele Frequencyが30%であるとすると、このSNPが暴露の分散をどれくらい説明するか？

回答)

$$
R^2=2\beta_x^2 MAF (1-MAF) = 2×0.15^2×0.3×0.7 = 0.009 = 0.9 \%
$$

Rule of thumb: F統計量<10は弱い操作変数の存在を示唆する
[E(F)>10でbiasが10%を超える]

しかし、現実的にはこのカットオフに頼りすぎることには問題がある。
第一に、操作変数の強さは「強い」「弱い」の二値に分けられるものではなく、連続的なものである。

第二に、このバイアスはone-sample settingで操作変数が3つ以上のときに関連する。操作変数が一つのときはバイアスは定義されない。操作変数が一つのときに暴露との関連がゼロとなることは考えにくく、操作変数による推定値は大きくなる。しかし、F統計量が5あればp≒0.03に相当し、バイアスの中央値はゼロに近づく。GWASで有意とされる基準 ($${p<5×10^{-8}}$$はF統計量30程度に相当する。

第三に、F統計量の計算はdata-drivenなので、例えばデータをみてF統計量<10の操作変数を除いて解析するようなアプローチを行うとかえってバイアスが増加しうる。教科書には、同じデータセットを異なる数に分割してF統計量の計算を試みた研究の例が記載されている。F統計量はサンプルサイズに依存するので、データセットを分割すると一つの分割単位毎に計算したF統計量は小さくなる。そこでF統計量＜10以下の操作変数を除外してpooled estimateを計算すると本来の値と異なる値が計算され、バイアスを生じうることが示されている。詳細は教科書の図を参照のこと。

Weak instument biasへの対処法

　weak instrument biasは操作変数の妥当性にも影響を及ぼす。もし2つの操作変数が同じサイズのpleiotropic effectを要すると、結果のバイアスはさらに大きくなる。交絡因子との関連が小さくても、重度のバイアスにつながりうる。
　MRのすべての手法が弱い操作変数の影響を受けるが、特に MR-Egger法はweak instrument biasの影響を受けやすくone-sample MRでweak instrumentを使用するときは推奨されない。
　weak instrument biasを減らすにはF統計量を増やせればよい。F統計量はサンプルサイズに依存するので、サンプルサイズを増やすことが対策となる。また、$${R^2}$$にも依存するので、暴露の分散の説明が小さい操作変数を除外するとF統計量は増える。これらの対処は理想的にはデータを収集する前に行われるべきである。
　複数のバリアント、アレルの値を要約したallele scoreを用いてあたかも操作変数が１つのように扱うことも、weak instrument biasへの対処法である。（上述したように操作変数が1種類のときにバイアスが定義されないため。）