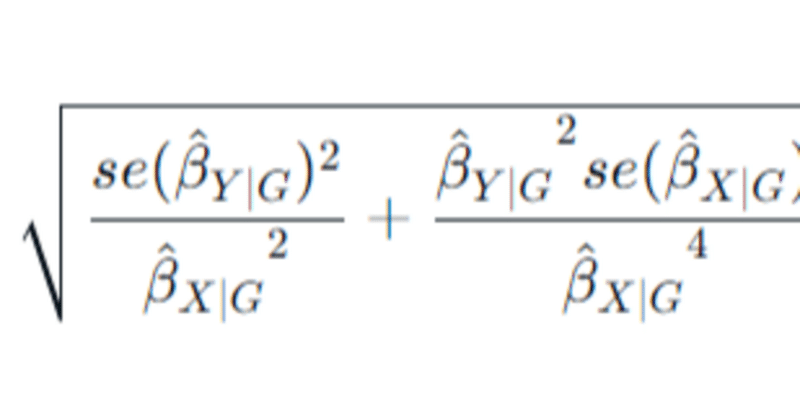
mendelian randomization
methods for causal inference using genetic variants chapter 4の勉強まとめ

Mendelian Randomizationを”MR”と略します。
Y: アウトカム, Outcome
X: 要因 (暴露), Exposure
U: 交絡因子, Confounder (often unmeasured)
G: 操作変数, 遺伝的バリアント Genetic variant as an instrumental variable
とおきます。

1. 係数比法

最も単純な方法

アウトカムが連続値, 操作変数が二値

遺伝的バリアントG が0 or 1 例(AA=0, Aa/aa=1)
$${ \={y_j} }$$ G=j (j=0,1)のときのアウトカムYの平均値
$${ \={x_j}, j=0, 1 }$$ G=j (j=0, 1)のときの暴露Xの平均値
とすると、因果効果は

$$
Ratio\:method\:estimate\:(dichotomous IV)=\frac{\vartriangle y}{\vartriangle x}= \frac{\={y_1}-\={y_0}}{\={x_1}-\={x_0}}
$$

と表せる。

アウトカムが連続値、操作変数が多くの値をとるor連続値

例） SNP がAA, Aa, aaのときそれぞれg=0, 1, 2とする
例)   操作変数をAllele scoreとして連続量としてとらえる (暴露との関連が線形であると仮定)

XのGへの回帰におけるGの係数を $${{\hat{\beta} _{X|G}}}$$と記載する。
$${{\hat{\beta} _{X|G}}}$$はXの一単位あたりの変化ごとのGの変化を意味する。

同様に、YのGへの回帰におけるGの係数を$${{\hat{\beta} _{Y|G}}}$$と記載する。

$$
Ratio\:method\:estimate\:(polytomous/continuous IV) = \frac{{\hat{\beta} _{Y|G}}}{{\hat{\beta} _{X|G}}}
$$

単純にβ係数の比で計算できるため、必ずしも個人データを必要とせず、summarized dataがあればよいと気づく。

アウトカムが二値のとき

Y=1 (例：疾患の発生) or Y=0
log linearityの仮定をおいて
$${{Y_j}}$$がG=jのときのイベント発生確率のlogとすると 

$$
Ratio\:method\:log\:risk\:ratio\:estimate\:(dichotomous IV)=\frac{\vartriangle y}{\vartriangle x}= \frac{\={y_1}-\={y_0}}{\={x_1}-\={x_0}}
$$

信頼区間

もっとも単純な方法は、正規分布に近似することである。
アウトカムが連続値のとき、最小二乗法を用いた標準誤差 (SE)と信頼区間を求める式は

$$
Standard\:Error\:of\:ratio\:estimate\approx\sqrt{\frac{{se({\hat{\beta} _{Y|G}})^2}}{{\hat{\beta} _{X|G}}^2} + \frac{{\hat{\beta} _{Y|G}}^2{se({\hat{\beta} _{X|G}})^2}}{{\hat{\beta} _{X|G}}^4}}
$$

ここで、$${se({\hat{\beta} _{Y|G}})}$$は$${{\hat{\beta} _{Y|G}}}$$の標準誤差を表す。
$${{\hat{\beta} _{Y|G}}}$$と$${{\hat{\beta} _{X|G}}}$$に相関がないという仮定が必要であり、相関を考慮した第三項を追加する式もある（割愛）が、practicalには推定が難しい。

また、GとXの関連の不確実性がGとYの関連と比較して小さい場合（$${se({\hat{\beta} _{X|G}})}$$が小さい場合)には、第二項を無視して第一項のみを用いた簡易式を用いることもできる。すなわち、

$$
Standard\:Error\:of\:ratio\:estimate\approx\left| \frac{{se({\hat{\beta} _{Y|G}})}}{{\hat{\beta} _{X|G}}} \right|
$$

しかし、いずれの仮定も正規分布することを前提としている。
サンプルサイズが十分大きくないときや、操作変数が"弱い"ときには過剰に狭い信頼区間の推定となることがある。

Fieller's theorem は操作変数が弱いときにはより好まれる方法である。
サンプルサイズをN、Nの自由度におけるt分布の97.5%パーセンタイル値を$${t_N}$$ (0.975) とすると(N>100のときは約1.96)

$$
f_0={\hat{\beta} _{Y|G}}^2-t_N(0.975)^2se({\hat{\beta} _{Y|G}})^2\\
f_1={\hat{\beta} _{X|G}}^2-t_N(0.975)^2se({\hat{\beta} _{X|G}})^2\\
f_2={\hat{\beta} _{Y|G}}{\hat{\beta} _{X|G}}\\
D=f_2^2-f_0f_1
$$

と定義したとき
もし $${D>0, f_1>0}$$ ならば95%信頼区間は $${\frac{f_2-\sqrt{D}}{f_1} }$$ から $${\frac{f_2+\sqrt{D}}{f_1} }$$となる。
$${D<0}$$ならば信頼区間は-∞から+∞までとりうる (弱い操作変数のとき)
$${D>0, f_1<0}$$ならば95%信頼区間は$${\frac{f_2+\sqrt{D}}{f_1} }$$から+∞までと-∞から$${\frac{f_2-\sqrt{D}}{f_1} }$$までを合わせたものである。このときアウトカムは暴露以外の原因で変化することが示唆され、操作変数の仮定に違反しているようである。
Fieller's theoremの計算ツール
https://sb452.shinyapps.io/fieller/

操作変数における検出力の低下

観察研究と比較して操作変数は妥当性を増すかわりに正確性が減り（信頼区間が広がる）、検出力が下がる。
サンプルサイズ計算のrule of thumbとして
従来の観察研究のNを操作変数が暴露を説明する係数で割る方法がある
例えば従来の観察研究で暴露とアウトカムの関連を示すのにN=400が必要であり、操作変数がその暴露のvariationの2%を説明するとき、MRで必要なサンプルサイズは400/0.2=20,000となる。

2. Two-stage models

1st stage: 操作変数→暴露の回帰
2nd stage: 1st stageでfitした暴露→アウトカムの回帰

アウトカムが連続値_最小二乗法 (2SLS)

操作変数が1つのとき、係数比法と最小二乗法は同じことをしている
操作変数が複数のときは、係数比法で求めた推定値の重みづけ平均を計算していると解釈できる。（ここでの重みは第一段階での操作変数→暴露の強さ）
操作変数がJ個あり、サンプルサイズがNとする。
$${i=1, 2, …, N}$$ で暴露が$${x_i}$$ アウトカムが$${y_i}$$
$${j=1, 2, …, J}$$で操作変数$${g_{ij}}$$とすると

1st stage regression modelの式

$$
x_i = \beta_0 + \sum_j{\beta_j g_{ij}+\epsilon_{Xi}}
$$

fitted model

$${{\hat{x} _i}=\hat\beta_0+\sum_k \hat\beta_k g_{ik} }$$

を2nd stage regression modelに用いて

$$
y_i = \theta_0 + \theta_1\hat x_i +\epsilon_{Yi}
$$

と表せる。 $${\epsilon_{Xi}}$$と $${\epsilon_{Yi}}$$は誤差項である。

関心のある因果効果のパラメータは $${\theta_1}$$である。

2SLS法の点推定値は正確だが、標準誤差は過小評価されている。なぜなら、２段階目の回帰において１段階目の不確実性が無視されているためである。
2SLSのソフトウェアは１段階目の不確実性も考慮に入れているため使用することを推奨する。

アウトカムが二値

log-linear or logistic regression modelを用いる
連続値のときと同様に推定値の標準誤差は過小評価される

3. 例　BMIと喫煙の強度

教科書にUK biobankのデータを用いた実践例が記載されており、割愛する。

4. 実践

STATA

ivreg2 y (x=g)

R

ivreg packageをインストールする
ivmodel.all = ivreg (y^x|g1+g2+g3, x=TRUE)
summary(ivmodel.all)
summary(ivmodel.all)$coef[2] #2SLS estimate
summary(ivmodel.all)$coef[2, 2] #SE of 2SLS estimate