統計学とは？なんでしょうか？履修を通じて自問自答してみました。
（その3「回帰分析」・「ベイズ統計学」）
 
３、回帰分析
 
回帰分析（regression analysis）は原因となる「変数」をいくつか設定し
一つの結果となる「変数」を求めるものだそうです。原因となる方を「説明変数」結果となる方を「被説明変数」と呼びますが、それ以外にも呼び方がいろいろあるらしいです。
「説明変数」が一つのものを「単回帰分析」と言い、複数のものを「重回帰分析」と言います。
この回帰分析のもっともわかりやすいのはこうしたグラフを見る事でした。

 サンプルデータに偏差が最も小さくなるような回帰線（回帰直線）を引くことです！それによって最も適切な関係のグラフが引かれます。グラフの図に書かれている式

がこのグラフを表すものですね。
回帰分析の優れているところは、関係の予測が出来るということです！
回帰分析はエクセルの「データ解析」で出来ます！
「データ」→「データ分析」（エクセルの右上の方にあります）→「回帰分析」
そしてX軸に説明変数をY軸に被説明変数（結果）を入れていきます。
エクセルの項目が書かれたラベルも選択した場合は「ラベル」にチェックマークを入れます。
それを出力するとあるデータが出て来ます！こんなのです！

 
ここで重要なのは「重決定R2」（ここの値が大きいと「説明力が高い」と言います）
そして「切片」はグラフの「０」の時のY軸の値。「X値１」とあるのは、例の回帰線の傾きの係数です！
そして
t値（これはー２～＋２の間にあると説明力が弱いと言われています。）
なのでこの表だと2.5、6.2なので（－２～＋２の範囲外なので）説明力があると言えます。
 
P値は、まさに確からしさの「probability」のPです！
この値の説明は、先生からは「効果なし」「係数０」（傾きがなく横に水平のグラフになります）を前提とした場合の生起確率ということなので。値が小さい時は「効果がある」と考えていいのではないでしょうか？
 
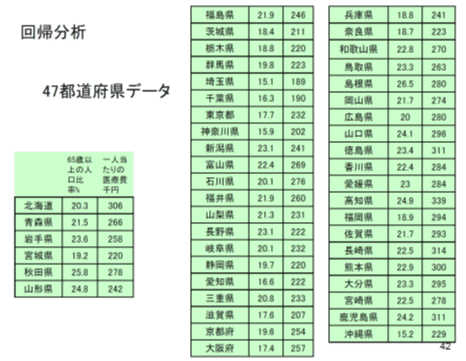
この回帰分析は日本全国の各都道府県の「65歳以上の人口比率%」と「一人当たりの医療費」との関係を分析したものです！そこには高齢者が多い地域は医療費が高いのではないか？ということの関係を調べようと言うところから分析が行われました！
授業のデータは以下のようなものでした。（K先生のスライドから引用）

 
重回帰分析　という分析もあります。これは説明変数が複数あるものです！
 
K先生の授業では、以下のお話が出ました。
1年間の被服費と家族数と所得の関係を分析しています。
これを見ると「家族数」が多いと被服費は上がる。
また「所得」が多いと少し被服費が上がるという関係がある種の説明力を持って証明されました。

これを見ると「重決定」97％とすごい説明力。左下の家族数の係数を見ると家族が1名増えると被服費が426上がり、所得が１増えると被服費は0.078の割り合いで増加します。ということがわかります！とても大きな要因の分析だったこともわかりますよね。
 
 
 
 

４、ベイズ統計学（ベイズの定理）
さていよいよラストの「ベイズ統計学（ベイズの定理）」です！本当の意味での統計学とは違うと言われているらしいのですが実践の現場でむちゃくちゃ使われている定理だそうです！説明が難しいのですが、教科書によると
 
「新しいデータを柔軟に取り込みことで、分析の正確さを向上させることのできる統計学。パラメーター自体の分布から推定値を検討出来る。」と書かれています。これで理解できる方はこれを読まなくてもええ人やと思います。私には何のことやらわかりません。
 
実はこのYouTubeとてもわかりやすいです！
予備校のノリで学ぶ「大学の数学・物理」の中の「ベイズの定理」です。
まずは、これをご覧ください

 
授業ではまずある事象の「事前の確率」があるのですが、その後「新たな情報」がやって来るとその確率が変わります。ベイズの定理は、その変化によって、さらにそれ以降の未来の確率がどのように変化するのか？ということを求めるものです。確率が変わることによって「経営戦略」も変化しますよね。その未来の「確率」をベイズの定理で導き、戦略のための武器にしていきます。
 
公式はこれです！

P(B|A) の逆確率である P(A|B) は、「P(B|A)と P(A) の積を P(B)で割る」ことで求められる。と書かれていました。これだけでは私はまったくわかりません。先生の資料を引用させていただきます。

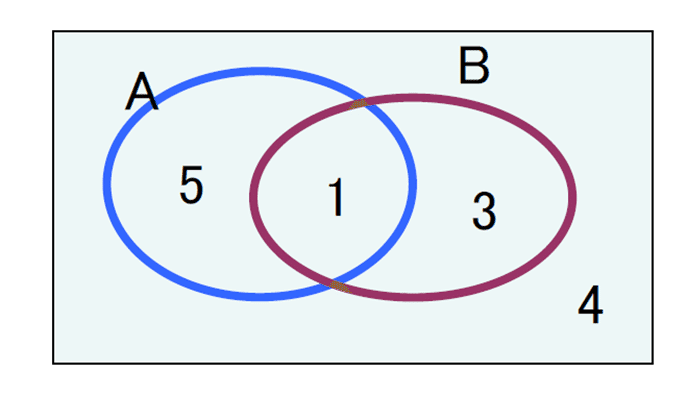
この「ベン図」はAには６つあって　Bと重なるものが１つ
Bには計４つあって　Aと重なるものが１つ
そして、AでもBでもないというのが４つ　計13個　のベン図です！
 
まず、P(B|A)はAの中でのBの割合（ここでは1/6）ですよね。
次にP(A)は=６/13ですよね。
P(B)は同じく＝４/13です。
 
ということは1/6×6/13÷4/13=0.25 となります。
 
P(A|B)＝Bの中のAの確率なので　Bの中は3＋１の4個　その内のAと交わっている確率が１つなので　1/4=0.25 でベン図で確認しても同じですよね。
 
これは、むっちゃ簡単なケースなので見ながら出来ます。
そのデータが複雑になってもこの公式を使って新たな確率を求めると予測できますよ！ということなのでしょうか？
 
まずは、表にまとめるとわかりやすいということで
ある方のノート（note）から引用させていただきます。
引用元：https://www.mynote-jp.com/entry/Bayes-and-table

以下の問いに対して
 
「薬物検査」
この薬物検査では，薬物の使用者の99%が陽性になり，非使用者の99%が陰性になる．また，社会全体の薬物使用者は0.5%であることがわかっている．この薬物検査で陽性だった人が薬物使用者である確率を求めよという問題。
 
筆者の方が作った表がこれです！

これを縦横でかけて計算すると

結果は

これなら手描きと電卓でも計算出来そうですよね！
面積もそれなりに比を計算して描いてあるのでわかりやすいです。
 
実際に検査で陽性になった確率と、その中のほんまの薬物使用者の割合がわかりますよね。
授業では
交通事故の証言の事例を学びました。
自分なりに表にして一覧できるようにしました！
この事例は、目撃者が（１）、続いて（２）と続く場合、それに応じて確率も変わります。
 
ある閉じられた島みたいな場所と仮定します。そこには、車は緑と赤しかなく緑が85％、赤が15％の割合。そして、目撃者の信頼性を80％とすると言う前提です！
目撃者１　が「事故を起こしたのは赤です！」と言った時の確率の変化
その後
目撃者2が「事故を起こしたのは赤です！」と言った時の確率の変化
が見えて来ます。

 
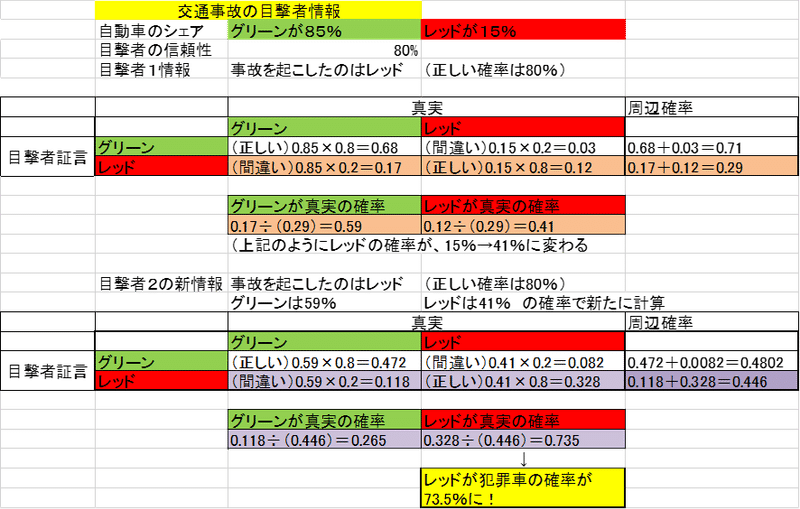
1人目が赤ですと言って「赤」の確率は表にもあるように　41％です！
（元々のクルマの配分の赤が15％からは大きく増えています）
2人目が同じく赤ですと言うと　その確率は　73・5％にアップしました！というような
計算をして確率を求めるのです！
 
これを授業では実際の、石油採掘の事例に置きかえて現場でこの定理がどう使われているのか？を学びました。
 
 
最後に統計のエクセル関数で、授業で出て来ただろうものを以下に記します。

（引用元：https://dekiru.net/article/4429/　）