こんにちは、辻村です。前回は、「RAIDのデータ復旧の仕組み（１）」と題して、簡単な足し算と引き算を使ってRAID-5の復旧の仕組みについてお話ししました。今回は RAID-6についてお話をしていきます。今回のお話は小学校の算数だけでは残念ながら解けません。中学校の数学くらいは必要です。最後の方で有限体（たい）のお話にも触れることになりますが、可能な限り専門的にならないようにお話ししたいと思います。

RAIDの仕組みをざっと知りたい方は、「壊れても耐える仕組み、RAIDについて」をお読み下さい。

はじめに

前回のお話の最後に、こんなことを書きました。

もし、以下の (1) の式が正しいとすると、(2) の式の答えが同じ6になるのも正しいわけです。従って、xとyというドライブの中身が入れ替わってしまっても、この式から入れ替わったことを知ることはできないわけです。

値が分かっていない変数が2つあるとき、少なくとも2つの変数の関係を説明する式が必要です。つまり、連立方程式を解くことになります。問題は、その式がどの様なものになるかと言うことです。
(1)が正しいときに、例えば次のような式があれば解けるのでしょうか？

少し考えていただくと分かるのですが、この方法では値を求めることもできませんし、どこに場所が入れ替わっても手がありません。ですから、少しばかり工夫が必要です。

前回ご説明したときに「RAID-5では、RAID装置内のディスクの位置が入れ替わっても検出することができない」とお話をしました。これらの問題を一体どう解決するのだろうと考えながら、読んでいただけると幸いです。

今回のお話の内容

今回のお話は、以下の順序でお話をしていきます。

・なぜ  RAID-6が必要⁈
・パリティが役に立たない⁈
・１ケタずつ割り振ってみる
・RAID-5と同じ方法で復旧できるケース
・Pとデータドライブ1台が故障した場合の復旧
・データドライブが2台故障した場合の復旧
・小数点がでちゃまずいのよ
・知らずに使っているガロア体？
・トリプルパリティの仕組み

なぜ  RAID-6が必要⁈

前回のお話で、それぞれのディスクにあるデータを排他的論理和（XOR）という計算で足し合わせたものをパリティとして使うとお話ししました。ドライブが破損したときには、残ったドライブにあるデータの値を合計し、それをパリティから引くことで、失われたデータが復旧できることについてお話ししました。

すべてのデータを復旧するには、復旧のためのデータとパリティをすべて読み出し、計算した結果を新しく交換したディスクに書き込むことになります。

HDDであれ、SSDであれ、どんなドライブでも寿命があります。いつかは壊れるわけです。データを保護する方法が必要ですが、RAID-5の場合、データ復旧中にもう1台のドライブが壊れれば、データは失われてしまいます。このような場合に備えて、一度に2台のドライブが壊れても保護できる仕組みが必要です。これが、RAID-6とかRAID-6相当の仕組みが必要な理由です。

パリティが役に立たない⁈

ディスクが2台壊れると言うことは、こんな式を解くと言うことと同じです。

この式を見ると分かるとおり、2つ問題があります。
・xとyが入れ替わっても合計は6になる。
・そもそも、この式だけでは解けない。

つまり、場所が特定できつつ、その式があれば解くことができる、そんな式がもう1つ必要なわけです。

１ケタずつ割り振ってみる

 問題を簡単に考えるために、それぞれのドライブには1つの値しか入らないとして、その範囲は 0 から 9 だとして考えてみましょう。また、PとQには正の整数なら何でも入るとします。あとでの説明のために、データの入るディスクは d0から d4 の5台とします。そして、図に示すために d4, d3, d2, d1, d0, P, Q の順番とします。

図1：　正常なデータとXOR計算されたPパリティ

5台のデータディスクの数字をじっと眺めていると、5桁の数字に見えてきませんか？ひょっとすると、それぞれのドライブに1ケタずつ割り振ってあげれば良いのではないでしょうか？Qについての計算は、単純にXORで合計するのではPと同じになってしましますから、それぞれの位（1の位や10の位）を重み付けとして掛けてあげましょう。つまり、d0に1、d1に10、d2に100、d3に1000、d4に10000と言う具合です。

上記の例でQを計算してあげると、以下の通りになります。

(5)の式は5、4、3、2、1という具体的な値の代わりにd4からd0の文字で表したものです。答えをQとしてあります。

よく見ていただくと、10, 100, 1000, 10000 は10の積です。つまり、10のべき乗です。通常 1は明示的に10のべき乗では書きませんが、10の0乗です。そして、それぞれのドライブの値をかけた形になっています。まず、添え字をつける形に(5) の式を書き直してみます。次に重み付けの値を10のべき乗で表現してみます。また、×の記号は書かなくていいので省略します。この操作が、(6)の式になります。

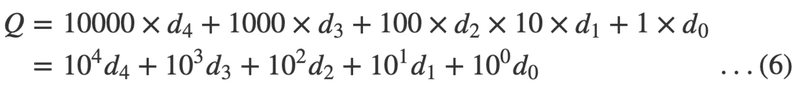
私たちは、10進数になじみがあるので、10を使ってきましたが、重み付けとして使う値は必ずしも10でなくても良いわけです。10と書いてあるところをgとおいて変数だけの式にします。

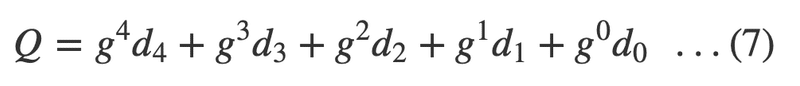
なんだか一気に数学っぽくなりましたね。でも思い出してください。やっているのはかけ算と足し算だけです。これを、ちょっと記号で書いてみましょう。さらに数学っぽくなります。

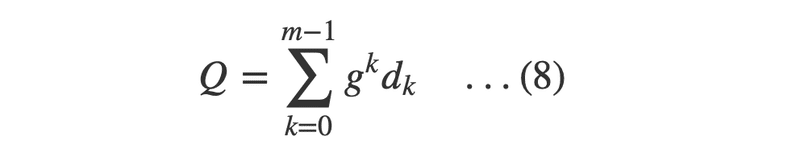
一見難しく見えますが、(7)の式の違いは、固定の5台であったドライブ数をｍ台に変えたと言うことです。5台の時に重み付けが gの4乗までであったと言うことは、m台のドライブがあるときには、0乗からm-1乗の添え字が重み付けとドライブにつくということになります。従って、この式の意味は、それぞれのデータドライブに対して、gが10であるならば、1から10のm−1乗の重み付けをして、それぞれのケタを計算し、合計すると言うことです。

具体的には、以下の作業をすることになります。

足したり、掛けたり、式を変形したりして辛抱強く付き合って頂きました。これでQが計算できました。ところで、一つお知らせがあります。Qを求めましたよね⁈これをリード・ソロモン符号と言います。そう、エラー訂正のQパリティそのものです。リード・ソロモン符号は、CDやDVD、ブルーレイなどで使われています。(*1)(*2)

ところで、(4)や(5)の式の形、見たことありませんか？そう、理論の基礎は簡単な多項式なのです。

RAID-5と同じ方法で復旧できるケース

実際に復旧する前に、簡単なケースをかたづけておきましょう。

RAID-6では、ドライブが壊れた場合壊れ方によって対処方法が違います。ここで「簡単に」と言ったのは計算がRAID-5の復旧と同程度でデータが復旧できるという意味です。なお、以下の説明で「データドライブ」とはパリティではなく実際のデータが入っているディスクドライブの意味です。

・データドライブが1台だけ壊れた場合

この場合は RAID-5と同様で、残りのドライブの情報から、XORを使ってデータドライブの内容を計算します。

・データドライブ1台と、Qが壊れた場合

RAID-5と同様にデータドライブを復旧したあとで、Qを計算し直します。

Pとデータドライブ1台が故障した場合の復旧

RAID-6ならではのひとつ目の復旧シナリオは、Pが故障し、さらにx番目のデータドライブが故障した場合です。この場合、Pを使ってデータを復旧することはできませんから、まず、残ったドライブで新しいＱであるQxを計算し、元のQから引くことで、データドライブDxを復旧します。ただし、出てくる値は、ケタを割り振るための重み付けがされているので、あとで、重み付けした値で割らないといけません。

Qはすべてのデータドライブの重み付けをした値の和ですから、壊れたドライブに入っているデータをDxとした場合、(9)の式になります。2行目の式は変形したものです。

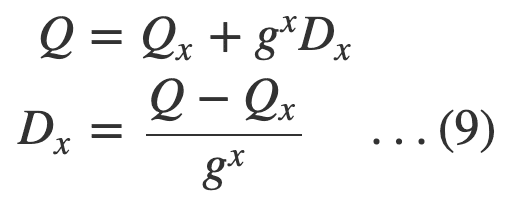
具体的な数字を入れてたどってみましょう。
今回の例では、Qは以下の通りとなります。

図2：　今回の例でのPとQ

仮にd4が故障し、Pが分からないとすると、Qxと重み付けしたd4の値は以下の通りになります。故障したドライブは値を0（ゼロ）として、Q-Qxを(9)の式から計算してあげると、以下のようになります。

d4には 10の3乗 (1000)の重み付けをしていたので、1000で割ってあげると無事に 4が復旧します。復旧後、改めてPを計算すると、Pも正しい値になります。

データドライブが2台故障した場合の復旧

データドライブが2台故障した場合を考えてみましょう。故障したドライブそれぞれのデータをDx、Dyと呼ぶことにしましょう。Pは残りのドライブからも計算できますが、生き残ったドライブから計算した結果をPxyとしましょう。また、Qパリティについても残りのドライブから計算し、これをQxyと呼ぶことにします。この時、以下の二つの式が成り立ち、データ復旧をするには、この連立方程式を解くことになります。

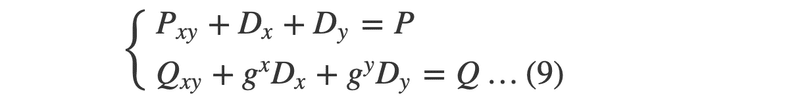
Pの式を変形すると、Dx + Dy は出すことができます。（(10)の式）ただし、これは、(1)と全く同じで、それぞれの値は、どちらも分かりません。そこで、Qの式を変形します。（(11)の式）

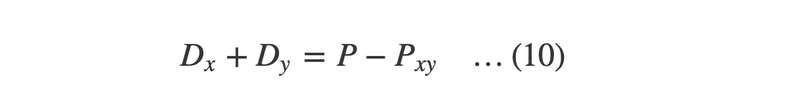
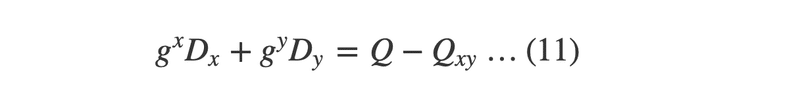
ここで、Qxyは2台故障した状態で、故障したドライブを０とおいたときに求められるQパリティです。(11)の式は、QとQxyの差がDxとDyにおのおの重み付けをしたものの和になることを示しているわけです。

さきほどの例（図2）を使って考えてみましょう。

仮に、 d2, d3 が故障したとします。すると、Qxyは以下の通りになります。

さて、ここから、Dxを求めるには、xの重みづけて割ってあげて、小数点以下を 切り捨てればいいわけです。

 小数点の上だけを考えると、4となります。めでたく、Dxは復旧できました。

次に、Dy は Q-Qxyから重み付けした Dxを引いて求めます。計算をしやすくするため、(11) の式を変形してみます。

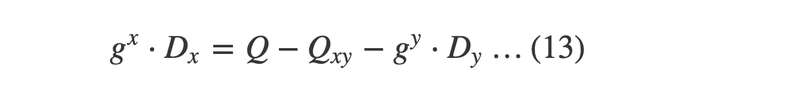
計算してみると、300になります。d2には100の重み付けをしていたので、3が求まり、d2の値が分かります。めでたしめでたし。

小数点がでちゃまずいのよ

残念ながら、そうはならないのです。3つ問題があります。

ひとつ目は、この話をするために、10進数で 0から9までが入ると仮定したことです。一方、コンピュータの世界では情報はビットやバイトという単位で扱われます。1ビットは2進数で1桁分、１バイトは8桁分です。1バイトで表現できる値は、私たちが日頃使っている10進数で表すと、0から255までです。つまり、ここまでお話をしたことが破綻なく1バイト単位で実現できないと困るわけです。

ふたつ目は、小数点の問題です。コンピュータの世界ではそもそも少数は存在しません。少数を扱うために浮動小数点などの仕組みを使って計算します。この場合、扱う値が、2で割り切れないような場合には、2の倍数に近いところに丸める必要があります。基本の単位が１か０のどちらかな訳ですから、仕方がありません。少数を表現するためには、浮動小数点などの方法を使って計算するわけですが、誤差が出ることがあると言うことです。

別の言い方をすると、2で割り切れなければ、実際の数字との差が出る可能性があるということなわけです。受け取る側が、異なる数字が出てくることを事前に知っていて考慮するか、許容することができなければ、正しくないデータということになります。ストレージシステムの場合、これは特に問題です。なぜなら、データを受け取る側は、「切り上げ」「切り下げ」などをすることなく、保管したデータがそのまま再現されることを前提にしているためです。

「2進数で表現しきれない値は、近い値を使う」ということを許してしまうと、誤ったデータを戻す可能性があるわけで、ストレージとしては問題です。

最後に、好みの問題と言われそうですが、割り算の時だけ小数がでてくるというのはどうもすっきりしません。

知らずに使っているガロア体？

改めて、計算に必要だった条件を整理してみましょう。

・０から２５５の数字が使える。
・加算（たし算）ができる。
・減算（ひきざん）ができる。
・乗算（かけ算）ができる。
・除算（割り算）ができる。
・多項式が矛盾なく書ける。
・（欲を言えば）整数だけで計算したい。

そういえばこんなことを私は以前言っていました。
（勉強していないのがバレバレです。）

数学の分野の一つに数論（すうろん）と言うものがあります。整数の集合を考え、その性質について研究する分野です。数論の中で「体（たい）」という考え方があります。

体（たい）は0で割ることをのぞき、加減乗除が自由に行える数の集合を指します。(*1)

身近な例では、実数の集合は体です。また、整数に分数を加えた集合は体を構成します。体に含まれる要素(*2）の数に限りがないとき、「無限体（むげんたい）」と言います。実数は無限にあるわけで、実数からなる体は無限体です。名前こそご存じなかったかもしれませんが、みなさん普通に使っていらっしゃるものです。

(*1) 有名な Division by zero （ゼロで割り算できない）のエラーはコンピュータで扱っている数字が「体（たい）」であるからです。
(*2) 元（げん）とも言います。

体（たい）のうち、含まれる要素の数が有限なものを「有限体（ゆうげんたい）」と言います。有限体の別名を発見者であるエヴァリスト・ガロアにちなんでガロア体と言います。もし、0から255の間の整数を取る有限体があれば便利です。

計算機の世界は 2進数だと言うことをお話ししました。幸いなことに2進数の1ケタ（1ビット）は、最も小さな有限体です。つまり、ゼロで割ることを除き、加減剰余が破綻せずに定義できます。（しかも2進数の特性から、加算と減算が同じに扱えたり、ビット計算で簡単に2のべき乗の計算もできます。）

いろんな方が研究してくださったおかげで、以下の多項式は g=2では2進数の世界で破綻しないことが分かっています。

（7の式を再度示します）

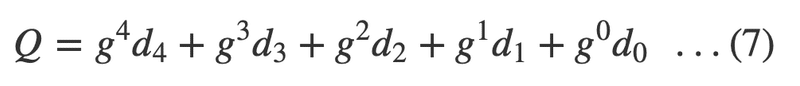
世の中の多くのリード・ソロモンの実装は、元（げん）の数は 2の8乗、つまり0から255までを使っています。これは元（もと）になった論文（A Tutorial on Reed-Solomon Coding for Fault-Tolerance in RAID-like Systems）が2の8乗を例にとって書かれているためと思われます。

リード・ソロモン符号はガロア体と多項式を使ったエラー訂正であり、CD、DVD、ブルーレイなどに使われています。つまり、みなさんも知らないうちにガロア体を使っているわけですね。

トリプルパリティの仕組み

近頃、トリプルパリティというものを耳にします。（RAID-Z3はトリプルパリティ相当です）トリプルパリティの場合、データディスクが同時に3台まで故障しても復旧ができます。考え方はここまでと同じですが、データドライブにP、Q、Rの3つのパリティがつくというものです。ここまでついてきてくださったみなさんには、Rの計算は実に簡単です。
（7の式を再度示します）

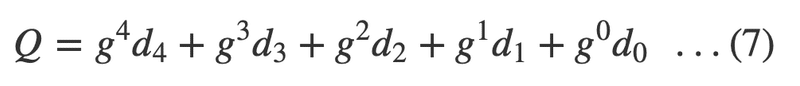
Qの実装は、g=2ですが、この式の g=4の場合がRです。
3台壊れた場合の復旧の計算はここでは示しませんが、同様に2進数の世界で破綻しないことが分かっています。

今回は書きませんでしたが、P・Qパリティの計算以外にも他の方法でパリティで計算する方法も存在します。もし興味を持たれるようでしたら調べてみEven-Oddやdiagnal parityなどのキーワードで調べてみてください。

つたない説明を最後まで読んでくださってありがとうございました。何かのお役に立てれば望外の喜びです。また、誤っているところを見つけられたら、遠慮なく訂正を入れてください。本当にありがとうございました。

参考文献

・The mathematics of RAID-6, H. Peter Anvin, 2007
・数学ガールフェルマーの最終定理、結城浩著
・A Tutorial on Reed-Solomon Coding for Fault-Tolerance in RAID-like Systems, James S. Plank
 ・Note: Correction to the 1997 tutorial on Reed–Solomon Coding, James S. Plank, Ying Ding, 2003
・Draft - 数式を書くのに活躍した結城先生のサイトです。
・Illumos ソースコード usr/src/uts/common/fs/zfs/vdev_raid.c のコメント

関連する記事

ハードディスクの障害解析について知りたい方は、以下の記事がご参考になるかもしれません。
・ディスクの障害の追いかけ方

RAIDの種類について知りたい方は以下の記事がご参考になると思います。
・壊れても耐える仕組み、RAIDについて

改版の履歴

・2020-02-08 数式・数字の訂正を含む見直し。
・2020-12-01 誤字・脱字のの訂正と読みやすさを考えての見直し。
・2021-03-08 誤字・脱字のの訂正と、体についてのコメントの追加。
・2022-05-06 「関連する記事」のセクションを追加