数学好きというものは、問題を解くことが好きであるだけでなく、問題を作り出すことも好きであったりする。役に立つかどうかは度外視して、身近な事柄でも面白いと思えば問題を作り、そして自分で解を模索する。傍からみればマニアック以外の何ものでも無いかもしれないが、マニアの側からすれば、それが楽しいのだ。
さて、ある日のこと、ふとひとつの問題を思いついた。自分の生年（１９６１年）にちなんで、１９６１という数字は、何か面白い性質を持っているのか、持っているとすればどのようなものか、という問題である。「面白い」というのは曖昧な表現で、凡そ数学の問題を設定するに当たって使用すべき表現ではないのだが、例えば「素数」であったり、「平方数の和」であったりすれば、自分としては十分面白いものの範疇に入れることができる。ここでは、個人的な興味によって問題を設定しているので、自分にとって「面白い」と思えれば良いものとして、話を進める。
さて、この１９６１という数字、一見して２、３、５では割り切れないことが分かるので、ひょっとしたら「素数」かもしれないという期待が持たれる。早速、調べてみることにする。もちろん、ネットで素数表を見てしまえばすぐに素数かどうか判定できるのだが、それでは面白くない。せっかくなので、エラトステネスのふるいに掛けていき、判定の過程も楽しむことにする。電卓やエクセルを使っても良いのだが、じっくりと楽しむには暗算に限る。７、１１、１３と順番に素数で割れるか確認をしていく。
割り切れる素数が見つからないまま、２９、３１と進んでいくがまだ割り切れない。残るは３７、４１、４３のみ。この三つで割り切れなければ１９６１は素数である。これはいけるかなと思った矢先、残念ながら３７で割り切れてしまった。１９６１は、３７×５３というふたつの素数の積であったのだ。しかしながら、これはこれでレアケースではないだろうか。１９００年代の１００年の内、３７より大きな素数同士の積で表されるのは、１９２７（４１×４７）しか存在しないのだ。１９６１はそれに次ぐ快挙といって良いだろう。我が生年、なかなかのものである。
今後もし、個人的なグッズをオリジナルで作るようなことがあって、その中に長方形の部分があるのなら、迷わず縦３７センチ、横５３センチにしよう。面積１９６１平方センチのミニ風呂敷でもつくろうか。
さて、素数の次は平方数の和に挑戦だ。ここから先はエクセルを駆使して効率的に作業を進めることにした。これも下の図中の二番目の式で示すように、４４の二乗と５の二乗の和で表現できることが判明。ピタゴラスの定理を使えば、直角を挟む二辺の長さが４４と５である三角形の斜辺の長さは１９６１の平方根となるわけだ。１９６１の平方根の作図をする機会があれば、この性質を使うこととしよう。（そのような機会など、有ろう筈がないとは思うが。）
その他にも、平方数の差、三つの平方数の和差、立方数による表現など、下図（３）～（５）に示すように１９６１はなかなか「面白い」性質を持っていることが判明した。これだけの結果が得られれば、とりあえず満足。こんな遊びなら、お金も一切かけずに楽しむことができるのだから良いことずくめ。ボケ防止も兼ねた老後の楽しみとして、数字遊びは打って付けである。

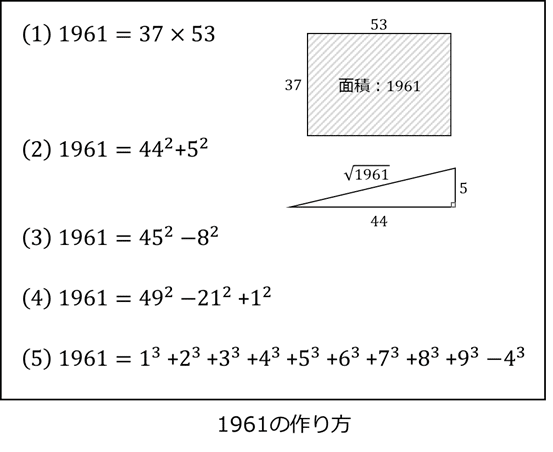
ところで、五番目の式だが、末尾の４の３乗の項は余計である。これがなければ、非の打ちどころのない「面白い」式であっただろう。逆に言えば、４の３乗である６４を１０６１に加えた２０２５年について言えば、この最後の項が外せることになる。そう思うと、２０２５年生まれが俄然羨ましく思えてくる。
しかも、この２０２５という数字、一見して２５で割り切れることが分かるので、試しに割ってみると商は８１となる。８１といえば、言わずと知れた掛け算九九の最後を飾る「九・九・８１」である。一方で２５の方は「五・五・２５」である。つまり２０２５は次の式でも表現することができる。

つまり、２０２５は平方数（４５の二乗）でもある。さらに、この式を見ていると、五の二乗の部分が気になる。五の二乗といえば、思い出すのがピタゴラスの定理の説明で良く出てくる次の関係式だ。

この式を使えば、次のような形に変形することができる。つまり、２０２５はふたつの平方数の和としても表現出来る訳だ。

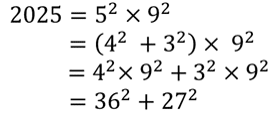
ここでさらに式を変形すれば、次のような式を得ることもできる。

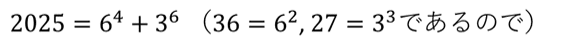
自分の生年ではないので、２０２５の分析はこのあたりで止めておくが、調べていけばまだまだ面白い性質が見つかりそうな予感がする。１９６１も面白かったが、２０２５も侮れない。ただし、１９６１にはもうひとつ、２０２５にはない性質がある。算用数字で書いた時に、下の図のように上下逆から見ても同じ（１８０度回転させても同じ）となる「点対称」な図形になる。これも「面白い」性質のひとつである。西暦でこのような数字は滅多に現れない。

このように、数字遊びには尽きることがない楽しみがある。点対称の西暦は他にどのくらいあるのか調べるもよし、ふたつの平方数の和で表すことができる西暦はどのくらいの頻度で出現するのか調べるもよし。芋づる式に新たな問題はいくらでも作ることができる。数学好きの興味の対象は尽きないのだ。