2つのボールをぶつけると円周率が分かる―論文を読まずに自力で計算してみた―
はじめに
2003年に以下のような興味を引くタイトル の論文が出ている。
G. Galperin, 2003. Playing Pool with π (The Number π from
a Billiard Point of View). Regular and Chaotic Dynamics, 8(4): 375-394.
タイトルにあるpoolとはいわゆるビリヤードのことで(この記事を書こうとして初めて知ったが)、タイトルを訳すと、「πで遊ぶビリヤード(ビリヤード視点からの円周率)」てな感じか。玉をぶつけると、その衝突回数から円周率が分かるという内容である。どういうことか?下図のように、水平面上にある2つの静止した玉を考える。
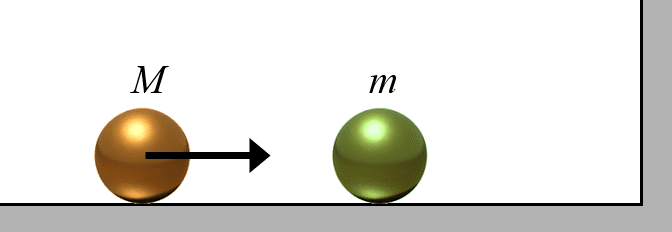
右の玉の右側に垂直な壁がある。左右の玉の質量をそれぞれ$${M}$$, $${m}$$として、左の玉の方が重い($${M>m}$$)とする。ここで、左の玉を右に転がすと、左の玉の方が重いため、右の玉は壁と左の玉の間で何度も衝突を繰り返す。左の玉は、右の玉に衝突されるたびに右方向の速度が減じていき、いずれ速度が左向きに反転する。最終的に、両方の玉が左に転がるようになり、衝突しなくなる。このような経過をたどることは、詳細な計算をしなくとも想像できると思う。
ここで最終的な状態に至るまでに、右の玉が左の玉と壁に衝突する回数を考えよう。2つの玉の質量が等しいとき($${M/m=1}$$)、右の玉は、最初左の玉に衝突され(今の場合、衝突後左の玉は静止する)、次に右の壁に衝突して反転し、最後に左の玉に衝突して静止して終わるので、衝突回数は3となる。左の玉が右の玉より重くなるほど衝突回数は多くなるが、この論文によると、何と、
左の玉が右の玉より100倍重いとき($${M/m=100}$$)、衝突回数は31
10,000倍のとき($${M/m=100^2}$$)、衝突回数は314
1,000,000倍のとき($${M/m=100^3}$$)、衝突回数は3141
となる。要は、$${M/m=100^n}$$のとき、衝突回数が、円周率の$${n+1}$$ケタの数字となるのである!(円周率は$${\pi=3.141592\cdots}$$)
何で??直観的にどうしてそうなるのかさっぱり分からないが、元論文は19ページもある大作で、数式を追う気にもなれない。ただ、主張する内容は分かりやすく、関係する物理も簡単そうなので、論文を読み込むより自分で考えた方が楽しそうである。実際、自力で計算してみたところ、確かにそうなった。単なる長い計算で、物理的に深い内容があるわけではないが、せっかく計算したので計算過程をここにアップしておく。使う数学は大学初年度レベルである(数学好きならば高校生でも可)。
問題の定式化
左右の玉の質量をそれぞれ$${M}$$, $${m}$$とし、$${M\ge m}$$とする。まず、エネルギー保存則と運動量保存則の式を立てよう。2つの玉の運動量を$${P_M}$$, $${P_m}$$で表す。速度・運動量の符号は、上図の右向きを正とする。玉Mの初速の運動量を$${P_0}$$とすると、エネルギー保存則は、
$${\displaystyle \frac{P_M^2}{2M}+\frac{P_m^2}{2m}=\frac{P_0^2}{2M}}$$・・・式1
である。標記を以下のように簡略化しよう。$${x=P_M/P_0}$$, $${y=P_m/P_0}$$とし、質量比を$${\varepsilon=m/M<1}$$とすると、式1は、
$${\displaystyle x^2+\frac{y^2}{\varepsilon}=1}$$・・・式2
となる。2つの玉が衝突が始まってから終わるまでこの式が常に成り立つ。以下で、この規格化した$${x}$$, $${y}$$を以下で「運動量」と呼ぶことにする。
次に、運動量保存則を定式化しよう。2つ玉同士の$${n}$$回目($${n}$$はあくまで玉同士の衝突回数であって、壁への衝突回数は含まない)の衝突直後の運動量を$${(x_n,\,y_n)}$$で表すことにすると、運動量はは以下のように遷移する:
mがMと$${n}$$回目の衝突直後:$${(x_n,\,y_n)}$$
次にmが壁と衝突した直後(mのみ向きが反転):$${(x_n,\,-y_n)}$$
次にmがMと$${n+1}$$回目の衝突の直後:$${(x_{n+1},\,y_{n+1})}$$
上記が任意の$${n}$$について成り立つので、運動量保存則は以下の式になる。
$${\displaystyle x_{n+1}+y_{n+1} = x_n-y_n}$$ for $${n=0\,,1\,,2,\cdots}$$(ただし、初期条件$${(x_0,\,y_0)=(1,\,0)}$$)・・・式3
終了条件はどうなるか?何回かの衝突を経て、最後に2つの玉同士が衝突した直後、Mが左向きに動いていて、かつ、mの速度$${y/m}$$がMの速度$${x/M}$$より遅ければよい(mの速度の向きは左右いずれでも可)。式で書くと、
$${x\le0}$$かつ$${|y|\le|\varepsilon x|}$$・・・式4
となる。
以上で問題の定式化が完了した。改めて整理すると、この問題は、以下のようになる。
$${0<\varepsilon\le1}$$とする。初期条件$${(x_0,\,y_0)=(1,\,0)}$$の下で、ゼロ以上の任意の整数$${n}$$に対して、
$${\displaystyle x_n^2+y_n^2/\varepsilon=1}$$・・・式2
$${\displaystyle x_{n+1}+y_{n+1} = x_n-y_n}$$・・・式3
の漸化式が成り立つとき、
$${x_n\le0}$$かつ$${|y_n|\le|\varepsilon x_n|}$$・・・式4
の2条件を満足する最小の$${n}$$を求めよ。
解法に入る前に、図解
上述したように、上記で求められる$${n}$$は、2つの玉同士の衝突回数であって、壁との衝突回数を含まない。壁との衝突回数を含む全衝突回数を$${N}$$とすると、$${N}$$と$${n}$$の関係はどうなるか?見通しをよくするために、点$${(x_n,\,y_n)}$$が、衝突のたびに$${xy}$$平面上をどのように動いていくかを考えよう。式2より、点$${(x_n,\,y_n)}$$は、常に下図のような楕円上を遷移していくことになる。
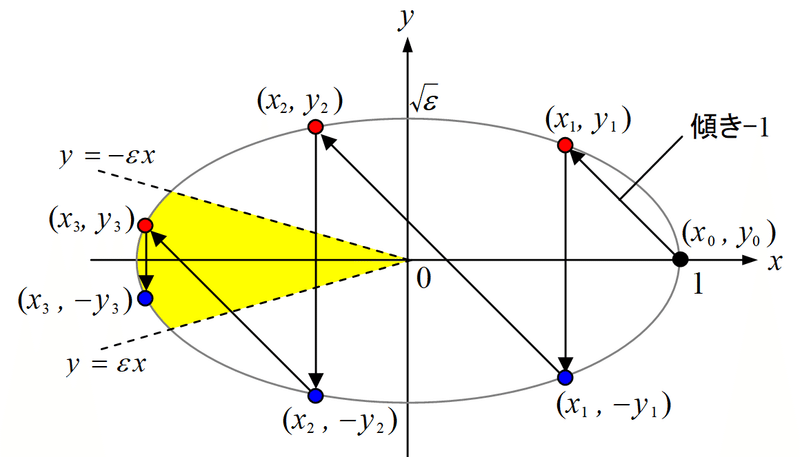
赤点は玉同士の衝突、青点は玉mと壁との衝突を表す。楕円の右端からジグザグに出発し、黄色の領域に入ったら、そこで終了となる。この例では、玉同士の衝突回数はn=3, 全衝突回数N=6である。
式3の意味するところは、点$${(x_{n+1},\,y_{n+1})}$$と点$${(x_n,\,-y_n)}$$は、傾き$${-1}$$の同じ直線上に乗るということである(ちょっと考えれば分かる)。これを踏まえると、衝突のたびに、点$${(x_n,\,y_n)}$$は以下のように遷移していく(上図参照)。
楕円の右端の点$${(x_0,\,y_0)=(1,\,0)}$$を出発点とし、そこから45°左上の方向(傾き$${-1}$$)に進む。
楕円との交点が、玉同士1回目の衝突直後の運動量$${(x_1,\,y_1)}$$となる。
次に、点$${(x_1,\,y_1)}$$を$${x}$$軸を中心に反転し、点$${(x_1,\,-y_1)}$$に進む(玉mが壁に衝突するため)。
次に、また45°左上(傾き$${-1}$$)に進み、上記を繰り返す。
上記のようにジグザグ遷移を繰り返して、黄色の領域(式4の条件)に入ったら、終了。
図2で赤点の個数=玉同士の衝突回数であり、壁との衝突回数を含む全衝突回数$${N}$$は、青点と赤点の個数の和となる。楕円の短軸と黄色の領域は、パラメータ$${0<\varepsilon\le1}$$で決まる。$${\varepsilon}$$を小さくすると、楕円が縦方向に潰れてくるため、$${N}$$の値は大きくなるのが分かるだろう。また、赤点の個数は、青点の個数と同じか、1つだけ多いかのいずれかである(図2では、青点が最後に来ているが、楕円の形状によっては、最後、赤点が黄色の領域に来て終わる場合もあることに注意)。この辺は後で再度精密に議論することにして、まずは赤点の個数$${n}$$を$${\varepsilon}$$の関数で表すことを目標としよう。
漸化式を解く
◆$${(x_{n+1},\,y_{n+1})}$$を$${(x_{n},\,y_{n})}$$で表す
$${R}$$を2x2行列として、
$${\displaystyle \begin{bmatrix}x_{n+1}\\y_{n+1}\end{bmatrix}=R\begin{bmatrix}x_{n}\\y_{n}\end{bmatrix}}$$
と表したい。式3を$${y_{n+1}}$$について解いて式2に代入すると、
$${\varepsilon x_{n+1}^2+(x_n-y_n-x_{n+1})^2-\varepsilon=0}$$
$${\varepsilon}$$の定数項を式2から$${\varepsilon=\varepsilon x_{n}^2+y_n^2}$$に置換して整理すると、
$${(x_{n+1}-x_n)\left\{(1+\varepsilon)x_{n+1}-(1-\varepsilon)x_n+2y_n\right\}=0}$$
となる。$${x_{n+1}\ne x_n}$$であるから、
$${\displaystyle x_{n+1}=\frac{(1-\varepsilon)x_n-2y_n}{1+\varepsilon}}$$
これを式2に代入して、
$${\displaystyle y_{n+1}=\frac{2\varepsilon x_n+(1-\varepsilon)y_n}{1+\varepsilon}}$$
を得る。従って、狙い通り、
$${\displaystyle \begin{bmatrix}x_{n+1}\\y_{n+1}\end{bmatrix}=\frac{1}{1+\varepsilon}\begin{bmatrix}1-\varepsilon & -2 \\ 2\varepsilon & 1-\varepsilon\end{bmatrix} \begin{bmatrix}x_{n}\\y_{n}\end{bmatrix}}$$
と書けた。$${\displaystyle R=\begin{bmatrix}1-\varepsilon & -2 \\ 2\varepsilon & 1-\varepsilon\end{bmatrix}}$$とおいて、上式を再帰的に適用して、
$${\displaystyle \begin{bmatrix}x_{n}\\y_{n}\end{bmatrix}=\frac{1}{(1+\varepsilon)^n}R^n \begin{bmatrix}x_{0}\\y_{0}\end{bmatrix}}$$・・式5
となる。
◆$${R^n}$$を求める
式5で、$${R^n}$$を求めれば、漸化式は解けたことなる。2x2正方行列の$${n}$$乗はどう求めるか?受験数学のテクニックを思い出そう。方法はいろいろあるが、ここでは簡単なケーリー・ハミルトンの定理を使う。同定理より、
$${R^2-2(1-\varepsilon)R+(1-\varepsilon)^2+4\varepsilon=0}$$・・・式6
が成り立つ。$${R^n}$$は、適当な$${n-2}$$次式$${Q(R)}$$を用いて、
$${R^n=Q(R)\left\{R^2-2(1-\varepsilon)R+(1-\varepsilon)^2+4\varepsilon\right\}+aR+b\\\quad\,\,\,=aR+b}$$・・・式7
と書けるはずである。実数の定数$${a}$$, $${b}$$を求めよう。そのために、以下の2次方程式を解く。
$${t^2-2(1-\varepsilon)t+(1-\varepsilon)^2+4\varepsilon=0}$$
2つの解$${t = 1-\varepsilon\pm2\sqrt{3}i}$$のうち一方を$${\beta=1-\varepsilon+2\sqrt{3}i}$$と置いて、$${\beta}$$, $${\overline{\beta}}$$(複素共役)を式7の$${R}$$に代入すると、
$${\beta^n=a\beta+b\\\overline{\beta}^n=a\overline{\beta}+b}$$
を得る。これを解いて、
$${\displaystyle a=\frac{\beta^n-\overline{\beta}^n}{4\sqrt{3}i}}$$
$${\displaystyle b=\frac{\beta\overline{\beta}^n-\overline{\beta}\beta^n}{4\sqrt{3}i}}$$
が得られた。これらを式7に代入することで、$${R^n}$$が求まり、それを式5に代入することで$${x_{n}}$$, $${y_n}$$が求まる。結果だけ書くと、
$${\displaystyle x_n=\frac{(\beta^n-\overline{\beta}^n)+\beta\overline{\beta}^n-\overline{\beta}\beta^n}{4\sqrt{3}i(1+\varepsilon)^n}}$$
$${\displaystyle y_n=\frac{\sqrt{\varepsilon}}{2i}\cdot\frac{\beta^n-\overline{\beta}^n}{(1+\varepsilon)^n}}$$
となった。$${x_n}$$$${y_n}$$は実数だが、上記の表式は虚数単位が入っていて複雑なので、もっと簡単な表式に直す。そこで、$${\beta=|\beta|e^{i\theta}}$$と極座標表示すると、
$${|\beta|=1+\varepsilon}$$
$${\displaystyle \theta=\arctan\frac{2\sqrt{\varepsilon}}{1-\varepsilon}}$$, $${\displaystyle \left(0<\theta<\frac{\pi}{2}\right)}$$・・式8
$${\displaystyle \sin\theta=\frac{2\sqrt{\varepsilon}}{1+\varepsilon}}$$, $${\displaystyle \cos\theta=\frac{1-\varepsilon}{1+\varepsilon}}$$・・式9
であり、これらを用いると、最終的に、
$${x_n=\cos n\theta\\y_n=\sqrt{\varepsilon}\sin n\theta}$$・・式10
となる。何と、これほど簡単な式になる!
◆式10の意味?
少し脱線するが、、、式10は、$${\theta}$$を媒介変数とした楕円の表式そのものである。下図参照。
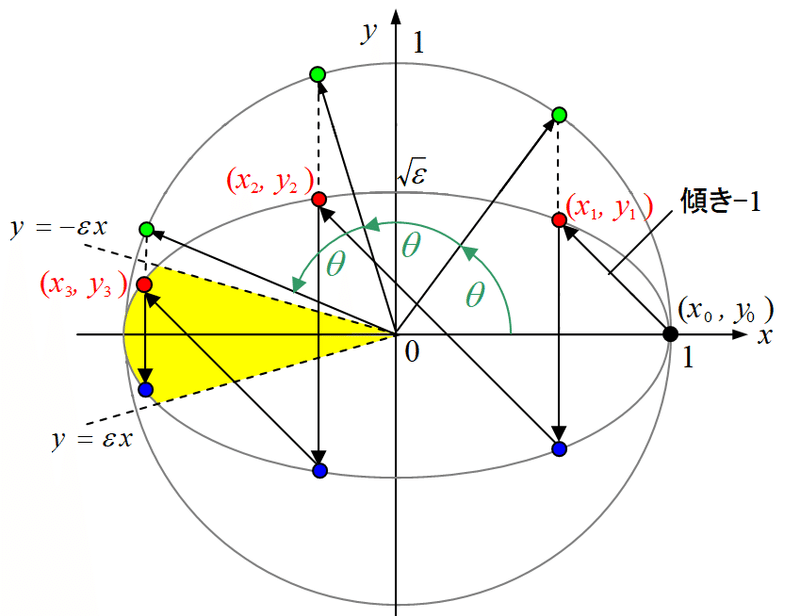
赤点は玉同士の衝突、青点は玉mと壁との衝突を表す。実は、外側に単位円上を等間隔に遷移する緑点が隠れている。
図2で説明したように、楕円右端の黒点を出発して楕円内をジグザグにたどれば点列$${(x_n,\,y_n)}$$は作図的に求められるが、実は、上図に示したように、この楕円に外接する単位円上を角度$${\theta}$$で等間隔に遷移する緑点が存在し、赤点の位置と同じ$${x}$$座標となるように対応していることを意味している。上図で、$${\theta}$$はあくまで単位円上の緑点が作る角度であり、楕円上の赤点が作る角度ではないことに注意。ジグザグにたどってできる赤点の背後にこのような性質が隠れているのは不思議ではないか??(自明ではないですよね、、、これ?)ただ、この問題の解法と直接は関係ないので、ここでは深入りしない。
終了条件を満たすnを求める
さて、$${(x_n,\,y_n)}$$の具体的な表式は式10の通り得られたので、終了条件を満たす$${n}$$を求めて、壁との衝突回数も含む全衝突回数$${N}$$を求めよう(個人的に、上記までの計算よりもこっちの方が頭を使った)。
終了条件(式4)間際の点列$${(x_n,\,y_n)}$$の動きを調べよう。終了間際では$${n\theta\simeq-\pi}$$であるので、1つ目の条件$${x_n\le 0}$$は自動的に満たされる。2つ目の条件$${|y_n|\le|\varepsilon x_n|}$$より、
$${|\sqrt{\varepsilon}\sin n\theta|\le|\varepsilon\cos n\theta|}$$
$${\therefore |\tan n\theta|\le \sqrt{\varepsilon}}$$
となる。この条件は
$${ |\tan (\pi- n\theta)|\le \sqrt{\varepsilon}}$$・・式11
としてもよい。ここで、終了条件近辺の様子を再度図示して見よう。
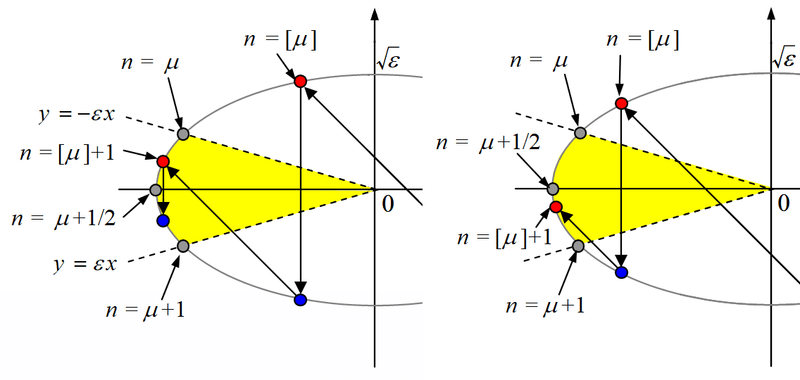
終了時は、赤点(玉同士の衝突)が$${y>0}$$に来て、折り返して青点(玉mが壁と衝突)で終わる場合(図4左)と、赤点が$${y\le0}$$に来て終わる場合(図4右)がある。赤点は、$${n}$$が大きくなるにつれて楕円の上側の弧を左回りに飛び飛びに移動してくるが、ここで、仮想的に赤点がちょうど$${y=-\varepsilon x}$$との交点に来た時の$${n}$$の値を$${\mu}$$としよう。$${\mu}$$はほとんどの場合整数にならず、実数となる。$${n = \mu}$$のとき、式11の等号が成立するので、
$${\tan(\pi-\mu\theta) = \sqrt{\varepsilon}}$$・・式12
となる。以下で、$${\varepsilon \ll 1}$$の場合を考える。$${|\pi-\mu\theta|\simeq 0}$$であることも考慮して、
$${tan(\pi-\mu\theta) \simeq \pi-\mu\theta}$$・・式13
$${\theta\simeq 2\sqrt{\varepsilon}}$$・・式14
の近似が成り立つと仮定する。式12-14より、
$${\displaystyle \mu=\frac{\pi}{\sqrt{\varepsilon}}-\frac{1}{2}}$$・・式15
となる。また、赤点がちょうど$${y=0}$$となるときの$${n}$$の値は、$${\pi/\sqrt{\varepsilon}=\mu+1/2}$$となる。
さて、いよいよ全衝突回数$${N}$$(赤点と青点の全個数)を求めよう。まず、$${N}$$を$${\mu}$$で表すことを考える。ここで、ガウス記号$${[\mu]}$$を導入する。$${[\mu]}$$は、$${\mu}$$を超えない最大の整数を表す(要するに、小数点以下の切り捨て)。赤点が図4の黄色の領域に入る1つ前の段階の$${n}$$が$${[\mu]}$$となる。すると、以下が成り立つ。
$${\mu-[\mu]>1/2}$$のとき、図4左の状況になる。このとき、全衝突回数$${N}$$は偶数で、$${N=2[\mu]+2}$$
$${\mu-[\mu]\le1/2}$$のとき、図4右の状況になる。このとき、全衝突回数$${N}$$は奇数で、$${N=2[\mu]+1}$$
まとめると、
$${\begin{cases}N=2[\mu]+1 & \text{if\,\,}\mu-[\mu]\le 1/2 \\ N=2[\mu]+2 & \text{if\,\,}\mu-[\mu]> 1/2\end{cases}}$$
・・・式16
となる。一方、式12-14より、$${\pi-\mu\cdot2\sqrt{\varepsilon}=\sqrt{\varepsilon}}$$であるから、
$${\displaystyle \frac{\pi}{\sqrt{\varepsilon}}=2\mu+1}$$
となる。これの整数部分は、
$${\displaystyle \left[\frac{\pi}{\sqrt{\varepsilon}}\right]=[2\mu+1]\\\quad=[2\mu]+1\\\quad=\begin{cases}2[\mu]+1&\text{if\,\,}\mu-[\mu]<1/2\\2[\mu]+2&\text{if\,\,}\mu-[\mu]\ge1/2\end{cases}}$$
・・・式17
となる。式16と式17はほぼ同じ結果なので($${\mu-[\mu]=1/2}$$がちょうど成り立つときは無視する)、全衝突数は、
$${\displaystyle N=\left[\frac{\pi}{\sqrt{\varepsilon}}\right]}$$・・式18
の1つの式にまとめられた。この式から直ちに、冒頭で述べた性質
$${1/\varepsilon=M/m=100^n}$$のとき、衝突回数$${N}$$が、円周率の$${n+1}$$ケタの数字となる
が成り立つ!長い道のりだった。。
近似誤差の評価
以上の結果は、式13, 14の近似の下で成り立つものである。せっかくなので、この近似の誤差を評価してみよう。示すべきことは、近似なしの$${\mu}$$方程式
$${\tan(\pi-\mu\theta)=\sqrt{\varepsilon}}$$
の解$${\tilde\mu}$$と、近似ありの方程式$${\pi-\mu\theta=\sqrt{\varepsilon}}$$の解
$${\displaystyle \mu=\frac{\pi}{2\sqrt{\varepsilon}}-\frac{1}{2}}$$
の差分$${\tilde\mu-\mu}$$を$${\varepsilon}$$の展開式で表すことである。単なる面倒な計算であるため(本当にメンドクセ)、計算した結果だけ書くと、
$${\displaystyle \tilde\mu-\mu=\frac{\pi}{6}\sqrt{\varepsilon}-\frac{2\pi}{45}\varepsilon^{3/2}+\cdot\cdot\cdot}$$
となった。これを使うと、
$${\varepsilon=100^{-1}\Rightarrow \tilde\mu-\mu\simeq5.2\times10^{-2}}$$
$${\varepsilon=100^{-2}\Rightarrow \tilde\mu-\mu\simeq5.2\times10^{-3}}$$
$${\varepsilon=100^{-3}\Rightarrow \tilde\mu-\mu\simeq5.2\times10^{-4}}$$
となった。ざっくり、$${N}$$が$${[\pi/\sqrt{\varepsilon}]}$$からずれる確率はこの程度のオーダーとなる。$${100^{-n}}$$の指数が大きいほど、ずれる確率は小さくなる。まあ、かなり精密に成り立つと言ってよいだろう。
おわりに
以上、長い計算だったが、おもしろい問題でした。この問題の物理的なエッセンスは式18にある。全衝突回数が、2つの玉の質量比の平方根に比例して、しかも、その比例定数が円周率になるというのは、なかなか意外性のある結果である。ここまで単純な式で書けると、同じ結果を物理法則からもっと簡単に導く方法もありそうである。それは宿題としてとっておく。
※2023.07.15追記。上記別解は本当に見つかった。下記記事を参照。
この記事が気に入ったらサポートをしてみませんか?
