植物の葉序フィボナッチの件、自力で証明してみた
はじめに
数学読み物でよくネタになるフィボナッチ数列というものがある。以下で定義される整数の数列である。
$${F_0=0, \quad F_1=1,\\ F_{n+2}=F_{n+1}+F_n\\\quad n=0,\,1,\,2,\cdots}$$
要は、$${n\ge 2}$$の任意の$${F_n}$$は、直前の2項の和で定義される数列で、
$${0,\,1,\,1,\,2,\,3,\,\,\,5,\,8,\,13,\,21,\,34,\\55,\,89,\,144,\,233,\,377,\,\cdots}$$
と続く。この数列に現れる整数をフィボナッチ数という。このフィボナッチ数が、植物の葉の出方や、ヒマワリの種の並び方に関係していることについては、検索すればいろいろ解説記事が出てくるので、ご存じの方も多いと思う。しかし、その手の解説のほとんどは、ある数え方をするとフィボナッチ数が出現する不思議さを紹介するに留まっていて、なぜフィボナッチ数が現れるのか数学的な解説がないものが多い。
本稿では、植物の葉の出方を表す「葉序」(幼女ではない)を題材とする。詳細は後述するが、本稿で説明するのは、よく目にする命題
葉序にフィボナッチ性があると、葉の重なりが絶妙に小さくなる
の表面的な解説ではなくて、本質的な命題である
「葉の重なりが最小」と「葉序にフィボナッチ性あり」の数学的な同値性
の証明である。シミュレーションで描画して、葉序にフィボナッチ性がある場合に葉の重なりが絶妙にバラける様子を示した解説もあるが、それでは単なる経験則に過ぎず、葉序フィボナッチの必然性が証明されたことにはならない。数年前、頭の体操のつもりでこの問題をたまに考えたのだが、意外と難問で、証明を思いつくまで半年超を要した。もっと簡単な証明方が絶対あると思うが、同様の解説はあまり例がないと思われるので、ここで紹介する。
葉序とフィボナッチ数の関係
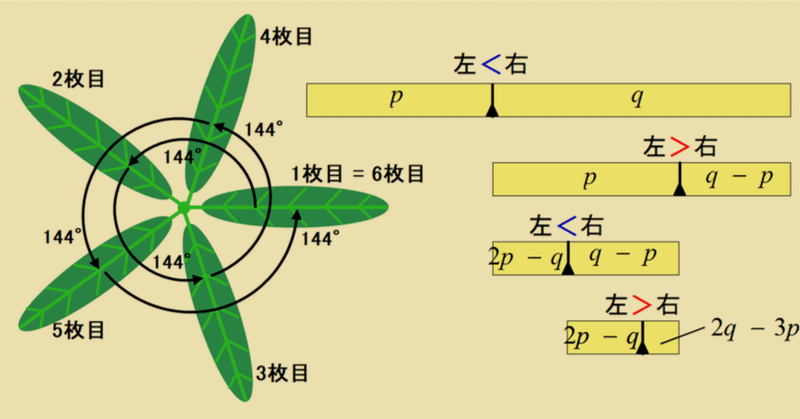
上に真っすぐ伸びる植物は、一定の角度間隔で葉を出すことが多い。茎を中心にして一定の角度間隔で葉を出して行き、何周かすると初めの方向に戻る。$${M}$$周する間に$${N}$$枚の葉を出すとき、その比$${M/N}$$を「葉序」という(幼女ではない)。葉序$${2/5}$$の場合の例を下図に示す。
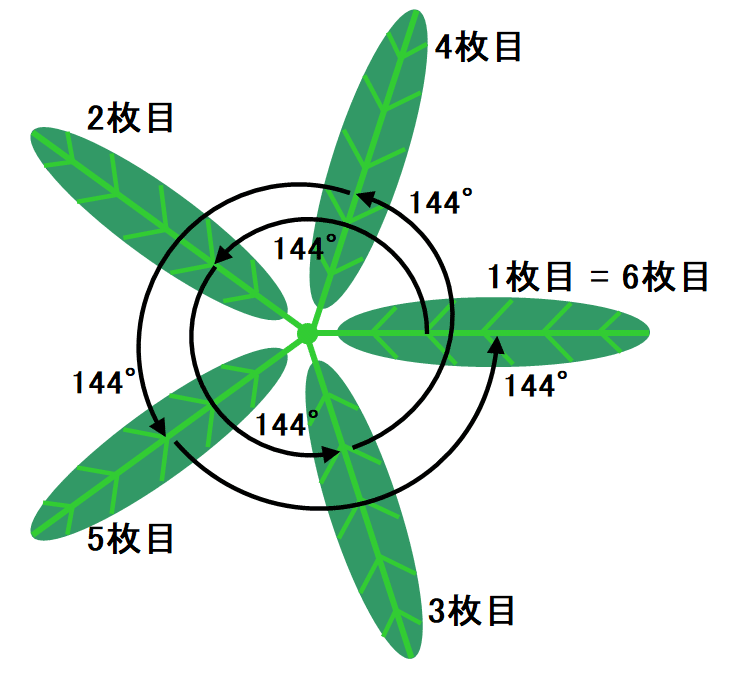
葉序2/5の場合、葉が出る角度間隔$${\Delta\theta}$$は、
$${\Delta\theta=2\pi\times 2/5 = 144\degree}$$
となる。上図では、葉の出る方向は、1枚目からスタートして、144°ずつ左回りに回転しながら葉を出して行き、2周して6枚目を出したところで最初の方向に戻る。2周する間に出る葉の枚数は5と数える(1枚目と6枚目はダブるので6枚目は数えない)。この葉序を表す整数$${(M,\,N)}$$は、$${(2, 5)}$$, $${(3, 8)}$$のように1つ置きの連続するフィボナッチ数の組になりやすい性質が知られている。
実際の植物で本当にそうなってるのか??その辺に生えていた直立型の雑草で確認したのが下写真である。

写真中の1の葉から数え始めると、3周して9枚目で元の方向に戻るので、この植物の葉序は3/8である。確かにフィボナッチ数である。
では、どうして葉序にフィボナッチ数が現れるのか?よくある解説は以下である。
(A) 葉が出る角度間隔$${\Delta\theta}$$は、360°を黄金分割した角度にとると、すなわち、黄金数$${\phi=(1+\sqrt{5})/2}$$を用いて、$${\\\quad\Delta\theta=2\pi/(1+\phi)\\}$$とすると、葉の重なり具合が最小になる
(B) 上記黄金分割の角度間隔を整数比の分割で近似しようとすると、葉序にフィボナッチ数が現れる
(B)の方はすぐに分かる(後述)。問題は(A)の方で、スッキリした証明が検索してもなかなか出てこないのである。注記しておくが、ここで問題にしているのは、あくまで、「葉の重なり具合が最小となる角度間隔$${\Delta\theta}$$を求めよ」という、純粋に数学的な問題である。植物の葉の形成器官の構造とか、葉序にフィボナッチ数を結果的に生じやすくしている生物学的な要因等については、ここでは関心がない。
(B)の証明
まずは簡単な(B)の方を証明しよう。
(B) 葉が出る方向の角度間隔を角度$${2\pi}$$の黄金分割に近似しようとすると、葉序にフィボナッチ数が現れる
[証明]葉序を$${M/N}$$($${M}$$, $${N}$$は互いに素)とし、葉が出る角度間隔を$${\Delta\theta}$$とする。$${M}$$周する間に$${N}$$枚の葉を出すから、
$${\Delta\theta=2\pi M/N}$$・・式1
が成り立つ。ここで、$${\phi}$$を黄金数
$${\displaystyle \phi = \frac{1+\sqrt{5}}{2}=1.618\cdots}$$
とする。黄金数の定義から、
$${\phi^2=\phi+1}$$・・式2
が成り立つ。さて、整数$${M}$$, $${N}$$をうまく選んで、角度間隔$${\Delta\theta}$$を角度$${2\pi}$$の黄金分割に近似させよう。この場合、
$${\displaystyle \Delta\theta=\frac{2\pi M}{N}\simeq\frac{2\pi}{1+\phi}}$$
すなわち、
$${\displaystyle \frac{M}{N}\simeq\frac{1}{1+\phi}=\frac{1}{\phi^2}}$$・・式3
が成り立てばよい(式2を用いた)。整数比$${M/N}$$を$${1/\phi^2}$$に近似させるには、どうすればよいか?ここで、フィボナッチ数列が登場する。フィボナッチ数列の一般項($${n\ge0}$$)は、黄金比$${\phi}$$を用いて、
$${\displaystyle F_n=\frac{\phi^n-(-\phi)^{-n}}{\sqrt 5}}$$・・式4
と書けるため、$${n\rightarrow\infin}$$のとき、第2項が消えて、
$${F_n\rightarrow\phi^n/\sqrt 5\,\,\,(n\to\infin)}$$・・式5
となる。従って整数$${M}$$, $${N}$$を、1つ置きの連続するフィボナッチ数
$${M=F_n\\\,N=F_{n+2}}$$
にとれば、式3が成り立つ。■
このように、葉が出る方向の角度間隔を角度$${2\pi}$$の黄金分割に近似しようとすると、必然的に葉序にフィボナッチ数が現れるのだが、連続するフィボナッチ数ではなく、1つ置きの連続するフィボナッチ数の組となるのがポイントである。
(A)の証明
さて、本丸の(A)の証明をしよう。
(A) 角度間隔$${\Delta\theta}$$は、黄金数$${\phi=(1+\sqrt{5})/2}$$を用いて、$${2\pi}$$の黄金分割$${\Delta\theta=2\pi/(1+\phi)}$$とすると、葉の重なり具合が最小になる
[証明]角度間隔$${\Delta\theta}$$の$${2\pi}$$に対する比を、分割比$${r}$$ $${(0< r <1)}$$と呼ぶことにする。「葉の重なり具合」を定量化できたとしたら、それは$${r}$$の関数で表されるはずなので、何とかしてそれを定式化して、$${r=1/(1+\phi)}$$のときに極小かつ最小となることを示せば良さそうである。ところが、分割比$${r}$$をいきなり実数として考えると難しく、さっそく行き詰ったので、整数比で分割することを考える。すなわち、2つの互いに素な整数$${a}$$, $${b}$$ ($${b > a > 0}$$) を用いて、
$${\displaystyle \Delta\theta = 2\pi r,\,\,\,r = \frac{a}{a+b}}$$・・式6
とする。$${\Delta\theta}$$は、$${2\pi}$$を$${a : b}$$に分けた角度とするわけである(下図)。以下で、起点となる1番目の葉を起点として、以後、ステップ$${n}$$に$${n}$$番目の葉が出るとする。$${a : b}$$に分ける場合、ステップ$${a+b}$$で、葉の出る全方向が出揃うので、そこで1周期分が終了する。
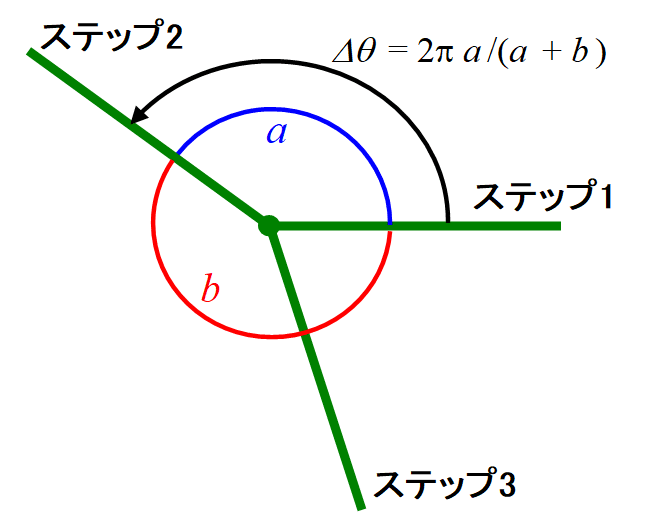
角度分割ダイアグラムによる表示
ここで、$${a}$$, $${b}$$に具体的な整数を当てはめて、各ステップにおける角度分割の様子を考えてみる。葉の出方を上から眺めた図だと分かりにくいので、以下のようなダイアグラムで表して考えよう。
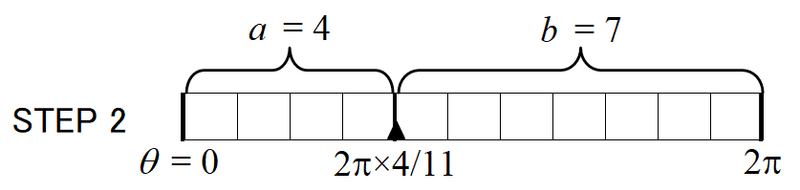
横軸は、葉の出る方向$${\theta}$$を表し、両端が、ステップ1の葉の位置$${\theta=0,\,2\pi}$$である。葉が出ている位置には太線を描き、新たに葉が出たところに▲を置く。上図は、2枚目の葉が出たステップ2の状態を表す。ステップ4まで表すと、下図のようになる。
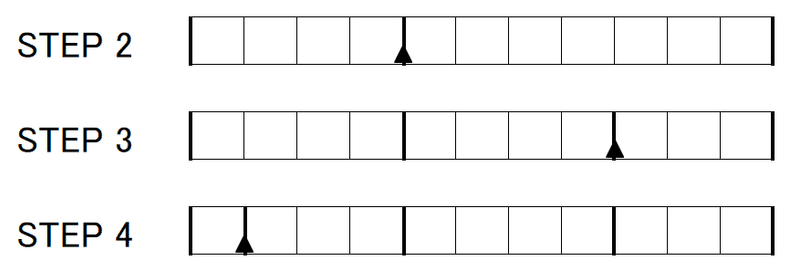
ステップ4まで表した。
ステップごとに、▲は右に4マスずつずれて現れる。右端に達したら左端にワープして繰り返す。全方向に葉が出た終状態のステップ11まで表したのが下図である。
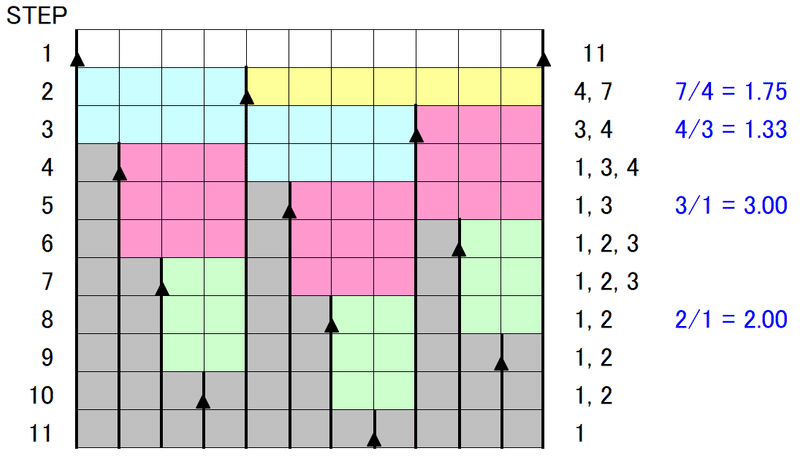
終状態のステップ11まで表した。
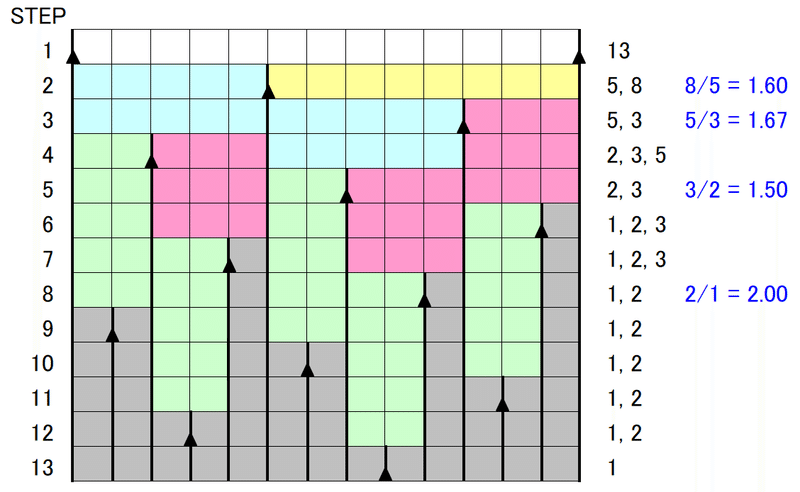
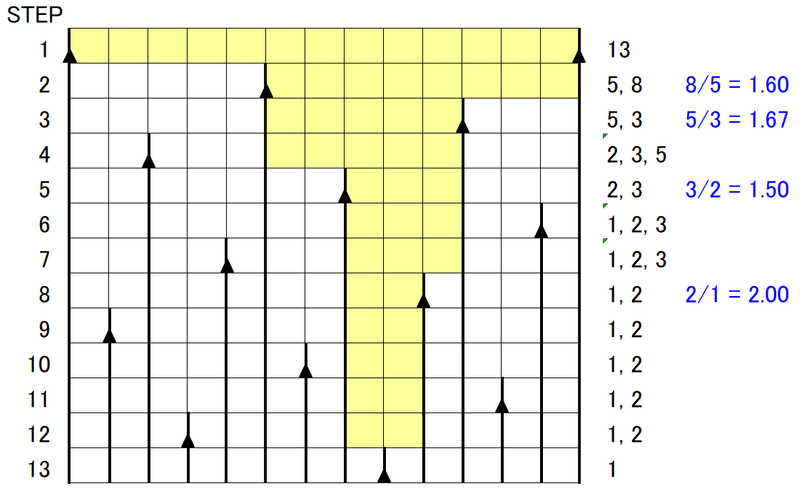
上図で、ダイアグラムの右に追記した黒字の整数は、そのステップにおいて存在する線分の長さである(ここで、隣接する三角形に挟まれた一繋がりのマス列のことを「線分」と呼び、そのマスの個数をその線分の「長さ」と呼ぶことにする)。上図では、線分の長さごとに色分けしてある。ステップ1で長さ11の線分ができ、ステップが進むごとに、それが分割されて行き、長さ1の線分のみになったら、そこで終了である。同様にして、$${a}$$, $${b}$$が連続するフィボナッチ数である$${a = 5}$$, $${b = 8}$$の場合を下図に示す。
「葉の重なり具合を最小にする」とは、この角度分割ダイアグラムを眺めたときに、どのステップにおいても、分割線(縦の太線)が横方向にできるだけまばらになるようにするということである。
図6, 7を眺めると、$${a}$$, $${b}$$の値に依らず、以下の(i)~(iv)の4つ性質があることが分かる。
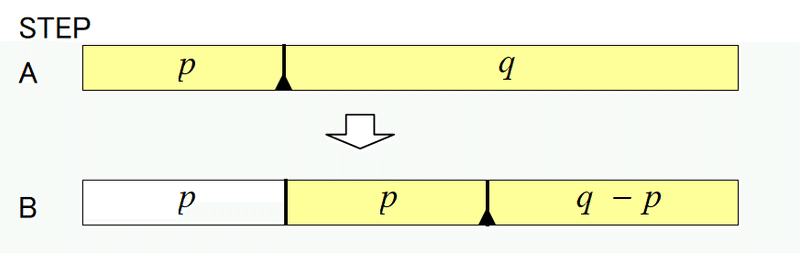
(i) 同じ長さの線分は全く同じように分割されて行く。
(ii) あるステップである長さの線分が長さ$${p}$$, $${q}$$ $${(p < q)}$$の2つの線分に分割されたとき、分割後の長さ$${q}$$の線分は、後のステップで長さ$${p}$$と$${q-p}$$の2つの線分に分割される。このときに生じる長さ$${p}$$の線分は、元の長さ$${p}$$の線分と隣接する。
(iii) 任意のステップにおいて、存在する線分の種類は高々3種類しかない。
(iv) あるステップで3種類の線分が存在するとき、後のステップで、最長の線分が分割されて、線分の種類が2つになるときが必ずある。
(i)が言っているのは、例えば下図(図7と同じ)において、2つある青線で囲った部分の内部のカラータイルの配置が完全にコピーになるということである(3つある赤線で囲った部分でも同じ)。これは、▲が一定の間隔で右にずれながら配置されて行くことを考えれば、必然的にそうなるのは分かるであろう(もしそうならないとすると、ダイアグラム中の▲の整然とした配置が不規則に乱れる)。
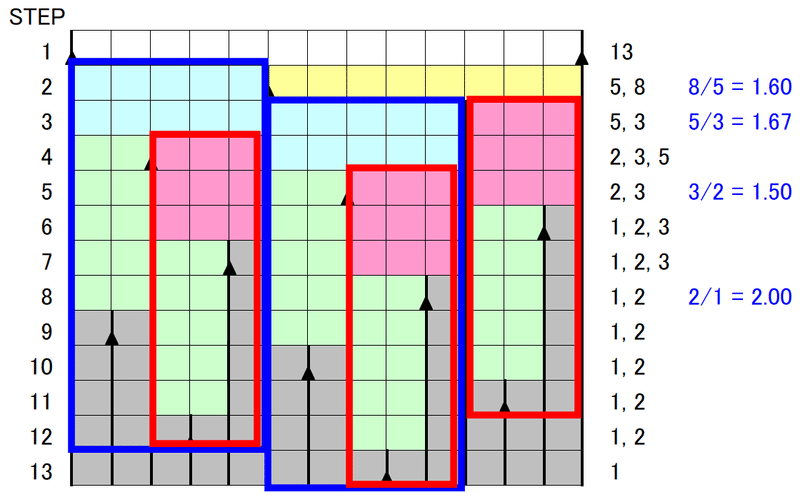
(ii)が言っているのは、例えば下図のように、ステップAで、ある線分が$${p : q\,\,(p < q)}$$に分割されたとき、分割後の2つの線分のみに着目すると、後のステップで次に現れる分割は、必ずステップBのようになるということである。新しい線分$${p}$$が、元の線分$${p}$$に隣接するように現れる。線分$${p}$$, $${q}$$の外側の状況とは無関係に、必ずこうなる。自明というほどではないが、図6~8のダイアグラム上で、▲が規則正しく斜めの格子状に並ぶことを考えると、そうなるのは分かる。
(i), (ii)を認めれば、(iii), (iv)は自動的に成り立つ。
葉の重なり具合の指標化
上記(i), (ii), (iii), (iv)の性質から、葉の重なり具合を考えるときは、下図のように、各ステップにおいて、その時点で最長の線分が分割される様子を辿って行けばよく、外側にあるその他の線分については気にしなくてよい(どうせ同じ構造のコピーだから)。
最長の線分を辿った部分を黄色で示した。
さて、葉の重なり具合を表す指標として、各ステップにおいて、その時点で
最長の線分を分割するときの分割比
$${K =}$$ [分割後の長辺の長さ] / [分割後の短辺の長さ]
を用いることにする。例えば、図7, 8, 10で、
ステップ2では、線分の長さは5と8があるので、$${K=8/5=1.60}$$
ステップ5では、線分の長さは3と2があるので、$${K=3/2=1.50}$$
である。図6~8, 10で、$${K}$$の値をダイアグラムの右側に青字で示してある。
葉の重なりを最小にするということは、全てのステップで、この$${K}$$値をできるだけ小さく抑えることと同値である。例えば、図6($${a=4}$$, $${b=7}$$)では、ステップ5で最大値$${K=3}$$があり、一方、図7($${a=5}$$, $${b=8}$$)では$${K=2}$$が最大であるため、図7の方が葉の重なりは小さい。このように、$${K}$$値を使えば、任意の$${a}$$, $${b}$$の場合で、葉の重なり具合の定量的な比較が可能になるわけである。
葉の重なりを最小にするには?
証明も佳境に入ってきた。上記$${K}$$値を用いて、葉の重なりを最小にするためには、分割比$${r}$$(角度間隔$${\Delta\theta}$$の$${2\pi}$$に対する比)をどのような値に設定すればよいかを考えよう。
角度分割ダイアグラムの任意のステップで現れる適当な長さの線分があるとして、それが後段のステップで分割されて行く状況を考える(下図)。
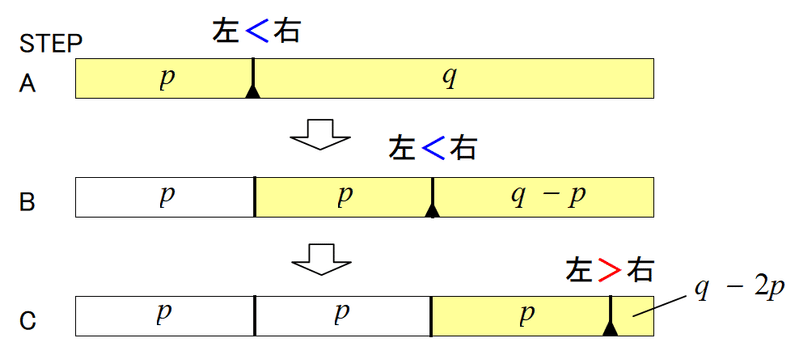
ここで注目するのは、線分の分割位置が、左右どちらに偏るか?である。上図で、ステップAとBでは左寄り、ステップCでは右寄りとなっている。この図のように、最長線分が連続して左寄りで分割されると、その結果として、後のステップで極端に右寄りの分割を強いられることになる。これが起きると、$${K}$$値がそこで大きな値に跳ね上がってしまう。
このような事態を避けるために、何がどうなっていればよいか?自分が考えてようやく到達した答えは、
最長線分の分割の左右の偏りが、毎回交互に入れ替わればよい
である。(下図)。
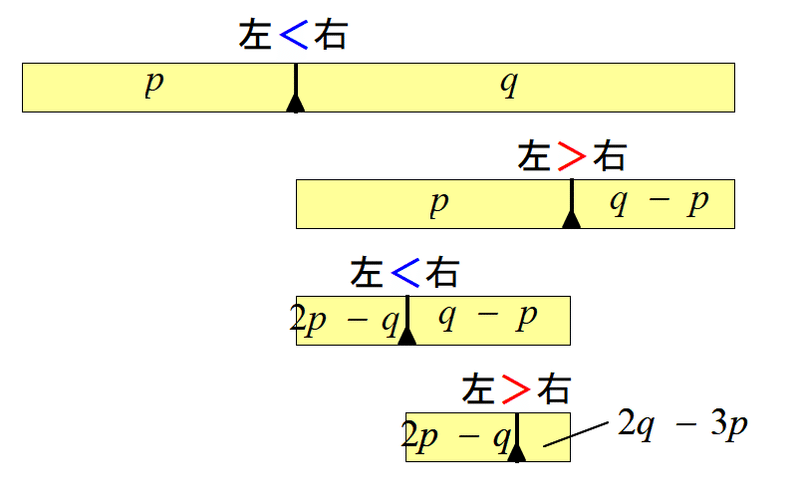
このような「左右交互分割」を実現するための、分割比$${r = a/(a + b)}$$($${a}$$, $${b}$$は互いに素、$${a < b}$$)に対する条件を求めよう。分割ごとに現れる左右の線分長を書き下すと、以下のようになる。各行の不等号の左右の値が、それぞれ分割後の左右の線分長を表す。
$${\begin{matrix} a&<& b \\ a&>& b - a \\2a-b &<& b-a \\ 2a-b &>& 2b-3a \\ 5a - 3b &<& 2b - 3a \\5a - 3b &>& 5b - 8a\\&\cdots&\end{matrix}}$$
このように書き下すと、$${a}$$, $${b}$$の係数にフィボナッチ数が必然的に現れる!葉序問題で、フィボナッチ数の暗躍を演繹的に炙り出した決定的瞬間である(胸熱)。
さて、上式の左右の線分長は、いずれかの段階で、両辺とも1にならなければならない。その条件は、ある整数$${n > 0}$$とフィボナッチ数を用いて、
$${F_{n+1}a - F_n b = F_{n+1}b - F_{n+2} a}$$・・式7
と書ける。整理すると、
$${(F_{n+1} + F_{n+2})a = (F_n + F_{n+1})b}$$・・式8
となり、フィボナッチ数の性質を用いて、
$${F_{n+3}a = F_{n+2}b}$$・・式9
$${\displaystyle\therefore \frac{a}{b} = \frac{F_{n+2}}{F_{n+3}}}$$・・式10
を得る。すなわち、$${a}$$, $${b}$$が連続するフィボナッチ数
$${a=F_n\\b=F_{n+1}\,\,\, (n \ge 2)}$$・・式11
となっていれば、「左右交互分割」は可能となる。また、フィボナッチ数の性質(式5)から、上式の右辺は$${n}$$が大きいときに黄金数$${\phi}$$に収束するから、式11の条件は、角度間隔$${\Delta\theta}$$を$${2\pi}$$の黄金分割の整数比近似で定めていることに他ならない。整数比で近似する限り、有限のステップ数の周期で葉が重なってしまうため、葉ができるだけ重ならないようにするためには、黄金分割の近似の精度を上げればよく、より大きなフィボナッチ数の比で分割すればよい。当然ながら、完全に黄金分割の場合に、葉の重なり具合は最小となる。■
以上で証明終わり(拍手!!)。
おわりに
確かに証明できたのだが、率直な感想は、
長い。。。
葉の重なりの指標化や、左右交互分割の条件を思い付くのにずいぶんと時間が掛かった。しかし、何か、難しく考えすぎてないだろうか?黄金比は対数螺旋とも関連するし、巧妙に作図して一目瞭然な証明法が絶対あるの思うのだが、残念ながら未だ思いつかない。改めて思うのは、この葉序フィボナッチの問題は、「よく知られているが、ちゃんとした証明はあまり知られていない(しかし、使う数学は高々高校レベル)」という、珍しいジャンルに属する。検索しても簡単に出て来ないのは、どういう論法でも結局難解になるからだろうか?英語の文献も検索すれば、さすがにもっと簡潔な証明が出てくるだろうが、しばらくの間、安易に検索したりせず、引き続き自分で考えるのを楽しむことにする。
この記事が気に入ったらサポートをしてみませんか?
