これまでの人生を振り返って、我ながら爆発的に集中力を発揮した瞬間が3回ある。

1回目は、大学入試2次試験（2日間持続）
2回目は、大学学部時代の「記号論理学II」のレポート課題（1週間持続）
3回目は、博士論文提出締切前（1ヶ月間持続）

単に多忙というのとは違って、没頭して頭がフル回転した感覚。集中から解放された後、どっと疲れが押し寄せてきた（特に3回目の後はひどかった）。いずれもほぼ大学時代に限定されているのは、就職してからは比較的イージーモードで乗り切っていることの裏返しか。本稿のネタは、上記2回目の時の話である。

清水義夫先生

当時、学部1, 2年生向けの一般教養科目で、清水義夫教官による記号論理学の授業があった。前半の「記号論理学I」と後半の「記号論理学II」に分かれるのだが、前半の方は通称「しみろん」とあだ名され、単位が取りやすい科目として認知されており、受講生も多かった（後半は内容が高度化するので、受講生は激減する）。この授業を担当した清水義夫教官が、今思い出してもすごい人だったのである。

当時既に50代後半だったと思うが、授業のときは飄々とした感じで教室に入って来て、授業中は独り言のように解説しながら大量の板書をすらすらと書いて行く。講義に緩急をつけて、時々学生の方に向き直って語りかけるようなことはほとんどなかった。今思い出しても、あの先生の笑顔を見た記憶はあまりないが、かと言って無愛想というわけでもなく、毎回飄々と登場して、飄々と超特急で板書・解説し、飄々と去って行くスタイルだった。

ある時気付いたのだが、この先生、講義の時、ほとんど手ぶらでやってくるのだ。持ってくるのは板書に使うチョークだけだったのである。

記号論理学という学問の中身は完全な数学で、授業中には大量の数式を板書するのだが、この先生は、何と、それらをすべて暗記（あるいはその場で導出）していたように見えた。

普通、理数系科目を担当する教官は、授業時は自作のノートを見ながら板書するものであり、手ぶら丸暗記で授業する教官を見たのは、後にも先にも清水義夫先生だけである（しかも、先生の専門は哲学！）。この先生の頭の中には、膨大な知識が完璧に整理されて入っているのかと思うと、世の中すごい人がいるものだと心底感心したのだった。

そんな飄々超特急スタイルの先生が、ごく稀に雑談気味に話したのが、いくつか印象に残っている。

「哲学の永遠のテーマは、自分探しです」

「デカルトの、『我思う、故に我あり」の論法は、実は、カントールの対角線論法です」

「私は、自分は数学者ではなく哲学者だと思っていますが、、最近流行っている『ゾフィーの世界』という本は、哲学者としてのプライドから、読んでおりません」（1995年に和訳が出版されたヨースタイン・ゴルデル著「ソフィーの世界」のことを言っているが、この発言の意図は忘れた。「ソフィー」を敢えて「ゾフィー」と言うところも意味ありげ）

記号論理学とは？

話を記号論理学に戻す。私はコレの専門ではなく、学部時代の授業で触れただけであるが、、私が理解しているところでは、記号論理学は、数学の理論を展開する際に用いる論理構成それ自体を研究対象とする学問で、全ての数学の最も土台となる部分である。数学というのは、どんな分野であれ、最初に、無証明に認める基本的な命題を公理として設定して、そこから様々な命題を論理的に導出して行く活動に他ならない、と言える。公理系をうまく設定して、また、ある命題から異なる命題を導くときに用いる推論規則もうまく定義できれば、数学の理論がもつ様々な命題は、原理的には公理を出発点として機械的な操作で導出できそうである。そもそも、このようなことは可能なのか？また、そのためにどのような公理系や推論規則を設定すればよいか？などを研究するのが記号論理学である。

記号論理学がおもしろいのは、その名の通り、考察対象を徹底的に記号化して取り扱うところである。どんな命題も、無味乾燥な記号列で表現される。言わば、数学の中でも抽象化の極致のような理論体系であるが、抽象的であるがゆえに、その応用範囲は広い。人間が行う「計算」という行為も、記号列の機械的な変換として扱われるため、それが後の計算機の基礎理論に発展している。

上記清水義夫教官の授業では、前半では命題論理・述語論理の基礎とそれらの代表的な公理系を学習し、後半では、述語論理の完全性定理、自然数を含む公理系の不完全性定理（さすがにこれはその意味と証明の概要だけ）、チューリングマシン等の計算可能性理論を学習した。私は、理解できたか否かはともかくとして、前半・後半両方ともそれなりに興味を持って履修して、特に後半の方は全部出席してきちんとノートを取った。

そして、後半の授業「記号論理学II」の考査として、レポート課題が出た。何でもよいので、講義内容を踏まえて自由にテーマを2つ設定してレポート用紙5枚以内程度にまとめて提出して下さい、というものだった。とりあえず、興味を持って自分で調べていた、記号論理学の発展の歴史をまとめるのを1つ目として、もう一つは、講義の内容で消化不良だった所から1つ選んで、自分で調べ直してまとめることにした。我ながら建設的なテーマ設定法である。

さて、何を選ぶか？消化不良だった箇所はいくらでもあったが、とりあえず、自分の興味もあってとっつきやすい、述語論理の完全性定理で疑問に思った式について考察することにした。それは、以下のような式である。

$${\displaystyle \vDash C_K \,\Leftrightarrow \,\,\,\vdash C_K}$$・・・式1

今思い出しても、この式の意味するところは分かりにくいので、一旦脇道にそれて、「不完全性定理」の方の話をする。

自然数論の不完全性定理

述語論理の「完全性定理」と、自然数論の「不完全性定理」は、いずれも、チェコ出身の数学者クルト・ゲーデルが1930年に弱冠24歳の若さで証明したものである。このうち、不完全性定理の方が、その意味することは個人的に理解しやすかった。定理（第1不完全性定理の方）を一言でいうと、

自然数論を含む述語論理の体系は、もし無矛盾ならば、形式的に証明も反証もできない命題が存在する

というものである。どういうことか？　

自然数論に限らず、一般に、数学の理論体系の論理構造というのは、以下のようになっている。

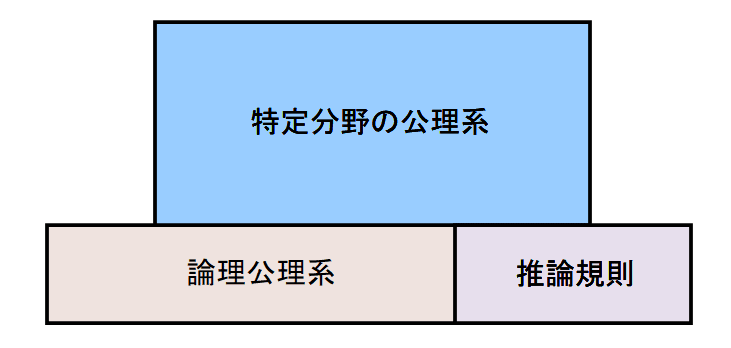
土台に述語論理等の論理公理系と推論規則があり、それに立脚して、数学の特定分野の公理系がある。「特定分野の公理系」には、群論ならば群論の公理系が入るし、自然数論ならば自然数論の公理系（ペアノの公理系など）が入るわけである。

このように数学の理論体系の基礎を整備した上で、数学の諸定理が、論理の出発点となる公理から推論規則に基づいた機械的な式変形をして、すべて形式的に導出できるか否か？という問題が、20世紀初頭、数学界で重大な関心事だったらしい。これは、例えるなら、自然数論における性質「4の倍数は2の倍数である」が、ペアノ公理系からの式変形で導けるか？というような問題である。この命題では簡単過ぎるが、自明でない極端な例なら、フェルマー予想（最終定理）で考えても良い（これも命題の表現は自然数論の範囲）。実際に成立するすべての定理が公理系から形式的に導出できるとき、その公理系は「完全である」という。

当時の数学界では、自然数論の公理系の完全性の成立について楽観的な見通しが支配していたようだが、そこにゲーデルが登場し、自然数論では完全性が成立しないことを証明したのである。その証明の中で、実際に、証明も反証もできない具体的な命題（ゲーデル文$${G}$$）を作って見せた。これが、当時の数学界に相当なインパクトをもたらしたらしいが、それを現代の自分が想像するのはちょっと難しい（正直、あまりピンとこない）。

とにかく、自然数論の不完全性定理というのは、自然数論を含む数学の体系において、任意の命題が、公理から出発して形式的に必ず証明できるとは限らない、ということである。不完全性定理の技巧的で難解な証明を辿るのはさすがに無理だが、とりあえず定理の言っている意味は理解できる。

述語論理の完全性定理

学生時代、理解に難渋したのが、述語論理の完全性定理の方である。この定理は、図1の土台部分に関するもので、一言でいうと、

述語論理の体系は、完全である

となる。上記の自然数論の体系とは違って、述語論理の体系では、内容的に正しい式は、必ず論理の公理系から形式的に導出できる（逆も成り立つ）。式で書くと、

$${\displaystyle \vDash C \,\Leftrightarrow \,\,\,\vdash C}$$・・・式2

となる。右辺の方は、

式$${C}$$が述語論理の公理系と推論規則から形式的に導出できる

という意味で、これは分かる。問題は左辺の方で、記号の意味をなぞると、

すべての解釈のもとで、式$${C}$$が真である

となるのが、これの意味を理解するのに苦労した。これを理解するには、「解釈」とか「モデル」とかの概念が必要になる。式2は、「形式的世界」と、意味を持つ「具体的世界」の対応関係を示す式となっている。

形式的世界と具体的世界の関係を図示すると、以下のようになる。

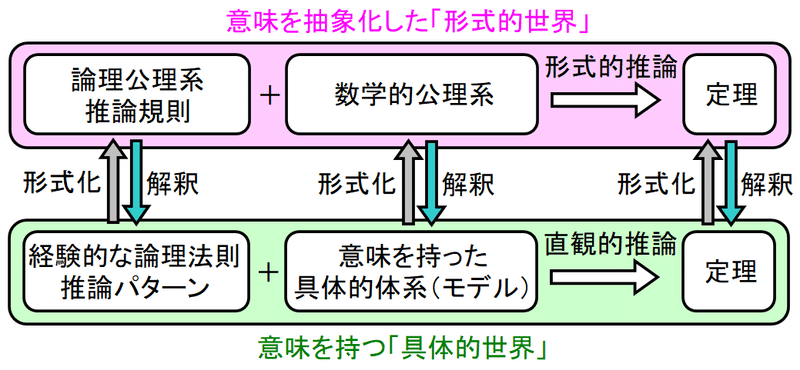
2層構造になっている下の世界が、意味を持つ「具体的世界」である。この世界では、考える対象は、自然数だったり、複素数だったり、3次元空間における正六角形の対称操作だったり等、具体的なモデルである。普通の数学はすべてこの世界で完結しており、経験的な論理法則によって、種々の定理が導出される。

2層構造の上の世界は、下の「具体的世界」から意味を取り去り、完全に抽象化した「形式的世界」である。この世界にあるのは、意味を持たない記号列で表される式のみである。論理公理系と、それに追加される数学的公理系を出発点として、推論規則に基づいて、記号列の機械的な操作によって、種々の定理が形式的に導出される。

2つの世界は「形式化」と、その逆の「解釈」によって対応付けられる。ここでポイントになるのは、1つの形式的世界には、複数の（場合によっては無限の）具体的世界が対応し、ある論理式が成り立つか否かは、対応させるモデルによって変わるということである。例えば、形式的世界にある

$${\displaystyle \forall x\,(\exist y\,(y < x))}$$（任意の$${x}$$に対して、$${y < x}$$となる$${y}$$が存在する）

という式は、整数のモデルを当てはめれば真となるが、自然数のモデルを当てはめると偽となってしまう。一方、

$${\displaystyle Px\supset \exist y\,(Py)}$$（$${x}$$が$${P}$$であるならば、$${y}$$が$${P}$$であるような$${y}$$が少なくとも1つ存在する）

という式の場合、具体的なモデルとしてどのようなモデルを当てはめても、必ず真となる。完全性定理の理解には、このようにモデルに依存せず必ず成立する式というのが重要なのである。

完全性定理
$${\displaystyle \vDash C \,\Leftrightarrow \,\,\,\vdash C}$$・・・式2再掲
の左辺は、述語論理の公理系をどのようなモデルに当てはめても、式$${C}$$は必ず真になる、ということを意味している。完全性定理の主張は、モデルに依らず成り立つ式は、論理の公理系から形式的にも導出できる、ということである。

式2から、直ちに、式1も導出できる。

$${\displaystyle \vDash C_K \,\Leftrightarrow \,\,\,\vdash C_K}$$・・・式1再掲

この式の意味するところは、述語論理の公理系に、さらに公理系Kを追加した体系を考えても、完全性定理と同じことが成り立つ、ということである。公理系Kは、例えば、上述した数学の特定分野の公理系を想定すればよい。公理系Kが、$${K_1, K_2, \cdots, K_n}$$のn個の式から構成される場合、上式の右辺は、

$${(K_1\land K_2 \land \cdots \land K_n) \supset C}$$・・式3

が、述語論理の公理系と推論規則から形式的に導出できることを意味している。上式の左辺の方は、

($${K_1}$$かつ$${K_2}$$かつ$${\cdots}$$かつ$${K_n}$$) が真ならば、$${C}$$も真・・式4

が、図2の具体的世界でどのようなモデルを想定しても成り立つことを意味する。

当時の疑問点

で、レポート課題の話に戻る。当時、上記のように形式的世界と具体的世界の2つの世界に分けて考えることや、モデル化の考え方も一応理解していたつもりだったのだが、それでも、式1の意味するところに非常に混乱したのである。式1は、述語論理の公理系＋特定の公理系K の体系で完全性が成り立つことを言っているのだが、公理系Kの選び方は任意なので、自然数論の公理系Nを選んでも、

$${\displaystyle \vDash C_N \,\Leftrightarrow \,\,\,\vdash C_N}$$・・・式5

が成り立つ。一方、ゲーデルは、自然数論Nを含む体系では、証明も反証もできない命題$${G}$$が存在するという「不完全性」を示したのではなかったか？　何か、矛盾してません・・・？？

式5の意味を書き下すと、

（自然数論の公理系がすべて真ならば、式Cも真）が、モデルに関わらず成立するならば、式Cは形式的に導出可能である（逆も成り立つ）

となるが、問題は太字の部分の意味である。括弧の中の部分がモデルに関わらず成立する、と言ったって、自然数論の公理系がすべて真でないといけないのだから、実質的に適用できるモデルは、自然数のモデルに限られるのではないか？

レポートの締め切り（確か1997年2月28日の正午）の1週間前から考え始めたのだが、当時、いくら考えてもこの疑問が解けなかった。清水先生の読みにくい教科書をいくら読み返しても分からず、図書館にこもって関連する本を探しても、レベルの高い本ばかりで手が出ない。頭の中がこの問題で一杯になり、完全集中のスイッチが入りっぱなしの状態で時間が過ぎていく。締め切りの前日、今日の昼間に答えが出なかったらレポート提出は諦めようと思いつつ、ダメ元で神田神保町の書泉グランデで数理論理学の専門書を探したら、野崎昭弘「不完全性定理　数学的体系のあゆみ」という入門書を発見！発刊は1996年9月20日で、まだ刊行間もない本だった。

本の最後の方にある完全性定理と不完全性定理の解説をその場で斜め読みして、自分の疑問点が一瞬で氷解した。

レポートは書ける！

急ぎ帰宅し、徹夜でレポートを書き上げ（当時は当然ながら手書き）、締め切りの1時間前に提出した。

自分が大きく勘違いしていたのは、

（自然数論の公理系がすべて真ならば、式Cも真）が、モデルに関わらず成立する・・（式6）

ことの意味である。私は、「自然数論の公理系がすべて真」となることが、すべてのモデルで成立することが必要であると考えたのだが、これが間違いだったのだ。

すべてのモデルで成立する必要があるのは、あくまで「自然数論の公理系がすべて真ならば、式Cも真」である。もし、あるモデルでは自然数論の公理系の少なくとも一部が真とならない場合、そのモデルでは、式Cは無条件に真となるので、気にしなくてよいのである（論理学の世界では、「AならばB」のAが偽の場合、Bは無条件に真となる）。従って、式6の条件は、想定するモデルに特に制限を課すわけではい。式5

$${\displaystyle \vDash C_N \,\Leftrightarrow \,\,\,\vdash C_N}$$・・・式5再掲

は、公理系として自然数論の体系を設定しても、それを当てはめるモデルとしては、自然数に限らず、全てのモデルで成立するような式Cに対して、完全性が成り立つことを主張している。制限が課されるのは、モデルではなく、式の方である。

では、不完全性定理との関係はどうか？　ゲーデルが示したのは、自然数論の体系に対して、具体的な対象として通常の自然数のモデルを当てはめた場合において、完全性が成立しないということである。自然数以外のモデルを当てはめた場合については何も言ってないので、矛盾ではない。

余談だが、では、自然数の公理系を全て真とするモデルとして、普通の自然数以外の数概念があるのだろうか？最近調べて知ったが、算術の超準モデルというのがあるらしい。

あるというだけ。理解できないが、とりあえず簡単に構成できるわけではないことは分かった。

おわりに

以上、思い出話。単なる小規模なレポート課題の話ではあったが、自分でテーマを設定して、自分で極限まて考えて、本の助けを借りつつも答えにたどり着いて課題を提出できたのは良い経験だったし、非常に達成感があった。その後、私は実験物理の世界に進んだので、記号論理は全く役に立ってないのだが、このような徹底的に抽象化・厳密化した数学の世界、人間の知的な営みの一端に触れられたのも、非常に良かった思う。

この辺の論理の話（数学全部かも知れないが）は、宇宙のどこかにいるかもしれない地球外知的生命体でも共通だと思うが、実際どうなのだろうか。意外にも、ここまで厳密で細かいことにこだわるのは人間の知性特有で、宇宙人の方は、もっと大らかで実用的な数学しか持ってなかったらおもしろい。論理の厳密化には、どの程度必然性があるのだろうか？この辺を考えると高度に哲学的な問いになる。清水先生の専門が哲学というのも、分かる気がするのである。