この記事では部分分数展開についてやってみようと思う。
まあ代数でいう部分分数分解を解析的に言ってるだけだと思ってもらえたらいいと思う。

この記事を読むことで受験生時代に覚えためんどくさい公式の意味を理解できると思う。

(例えば上のサイトに載ってる公式のようなもの)

このサイトから辿っていけば結局なぜそうなるのか分かるようになっているが、ここでは解析学として扱ってみる。

さっそく重要な定理を見てみる。
f(z)は有理関数であるとする。

証明は$${φ(z)=f(z)-(右辺)}$$を考えて、リウビルの定理(条件の確認は必要)を使って、z=∞の時を考えて$${φ(z)=0}$$で終わり。

さて、複素関数論を触ったことがある人ならこの時点で納得いただけたと思う。
なんで分母に2乗や3乗があるときに部分分数分解したときに2乗や3乗の項も必要なの？とよく思っていたけど、主要項だから必要なのか！と。

複素関数論を扱ったことがない人に簡単にだけ説明しますと。
正則でない点とは微分可能でない点と思えばよく、例えば1/(x-1)(x+1)ならx=1,-1と思えばいい。
そしてその点でローラン展開というTaylor展開を一般化したような特殊な計算をして、その主要項ってのを見てあげる。
そして∞の時の主要項も考えて、あとは足したら分解になってます！
そんな感じ。

まあそんなこと言われても分からねえ！って話だと思うから実際に計算してみましょう。

まあこんなものは普通に計算する方が圧倒的に早いのだが今回の形式に合わせて解いてみる。

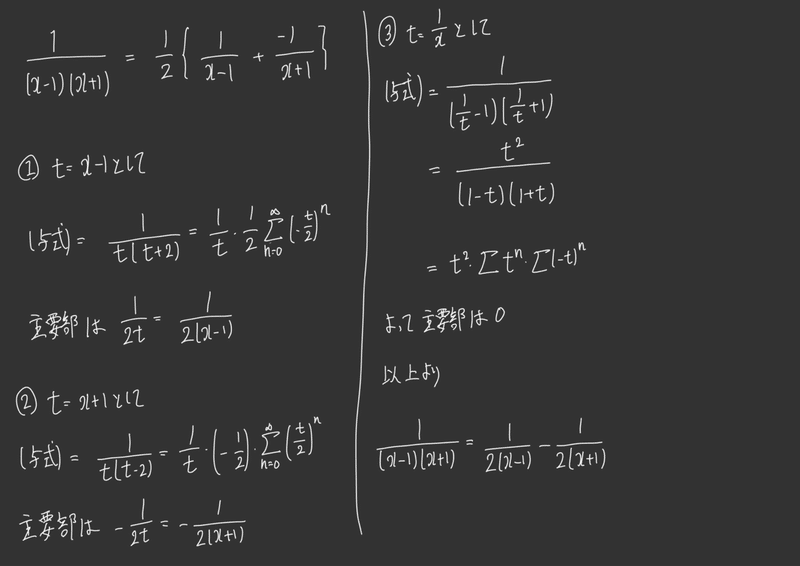
①ではx=1における主要部を
②ではx=-1における主要部を
最後③ではx =∞における主要部を考えている。
そして最後に足し合わせて、やっぱり普通に計算した結果と一致していることがわかる。

もちろんこれはたまたまではなくて理論的にこうなっている。
他の例も試してもらえると良いと思う。

複雑になってくるとTaylor展開(ローラン展開)が必要になってくるからその知識は必要なことに注意する。

あとがき的な

まあそれなりに書けたと思う。
まあせっかく複素関数論を習ったのだからそれについて書きたいと思って書いたのと、以前書いた代数学の基本定理もそうだが代数のことも解析で議論できるというのは面白いなと思って書いた。

と、いうかそもそも代数幾何解析という分類は人間が与えたものであって、元からあったものではないと思う。
だからその分野で完結せずに色々な分野を横断することは本来は自然なことだと思う。
そして代数的に式を色々触ってわちゃわちゃするのが楽しい人もいると思うが、このように解析的にパッと出来るのも楽しいと思う。

正則はともかく、ローラン展開や主要項などは複素関数論の中でも最後の方に出てくる概念であり今すぐ理解するのは難しい概念ではあると思う。
だがやってみるとCauchyの積分定理など美しいものともたくさん出会えるので、おすすめの分野です！

オマケ
さらに発展として...

では1/sin(z)などを部分分数分解してみるとどうなるだろうか？
主要部は有限項だが正則でない点は無限個存在する。
このような場合でも補正をかけてあげれば部分分数分解できることが知られている。
それを理解するには留数といった概念も必要になってくる。

さらにsin(z)は無限積で表せることも知られている。これを使うことでよく言われるバーゼル問題(逆数の二乗和がπ^2/6になる)というのがあるが示せるし、sinが関係しているからπが出てくると考えれば納得できる。

さらに統計などをしていると出てくるガンマ関数くん。
これも実部が0より大きいところでしか定義されていないが、複素解析を行うことで0以下の整数の点を除く範囲にまで広げることができる。

また現実における標準時子午線も分枝という形で現れる。
なかなか面白い。
が、とてつもなく難しい。
私は分枝のところは諦めた...