
空間とは何か(3) ユークリッド幾何学の空間概念
古代ギリシャにおける明証性の変革
「証明する」というギリシャ語δείκνῡμιの原義は「光のもとにさらけ出す」であるという。古代ギリシャでは、例えばタレスの幾何学5命題にもあるように、その初期の段階から幾何学の事実が命題化されていたが、その論証は視覚的な直観に訴えるものが多かったと考えられる。
タレスの幾何学5命題
命題1. 円はその直径(中心を通る直線)によって二等分される。
命題2. 二等辺三角形の2つの底角は相等しい。
命題3. 対頂角は等しい。
命題4. 2つの角がそれぞれ相等しく、それらに挟まれる辺が等しい2つの三角形は合同である。
命題5. 直径を辺とし円に内接する三角形は直角三角形である(直径の円周角は直角)。
(タレスの幾何学5命題の謎については、すでにこのnote有料マガジン内の記事でも扱っていますので、興味ある方は参照してください。)
すなわち、最初期の古典ギリシャ時代における幾何学では、図形の重ね合わせなどによる直観的・視覚的な明証性に依存した論証がなされていたと推定され、このことは多くの数学史家によって指摘されている。例えば、タレスの命題2は、二等辺三角形をその底辺に下した中線で折り合えすことで、底角が等しいことがわかるという具合である(図1)。

しかし、それからまもなく、紀元前5世紀頃の古代ギリシャでは論証数学における「論証」の意味に大変革が起こったらしい。すなわち、このような「視覚的・直観的な明証性」では論証としては不十分であり、視覚的な現実を離れた、より高次の論理的明証性を目指すようになった。その結果、紀元前3世紀頃のユークリッド『原論』では、上のような折り返しと重ね合わせによる明快な証明はすでに捨て去られ、三角形の合同の議論を幾重にも用いた、少々複雑な証明が付けられている。
実際、二等辺三角形の底角が等しいという命題のユークリッド『原論』における証明(第1巻命題5)は、中世ヨーロッパの大学では「ロバの橋」と呼ばれた。その理由は、図が橋に似ていること(図2)、さらにロバ(=愚か者)は渡ることのできない橋(=理解することができない証明)だとされたからである。
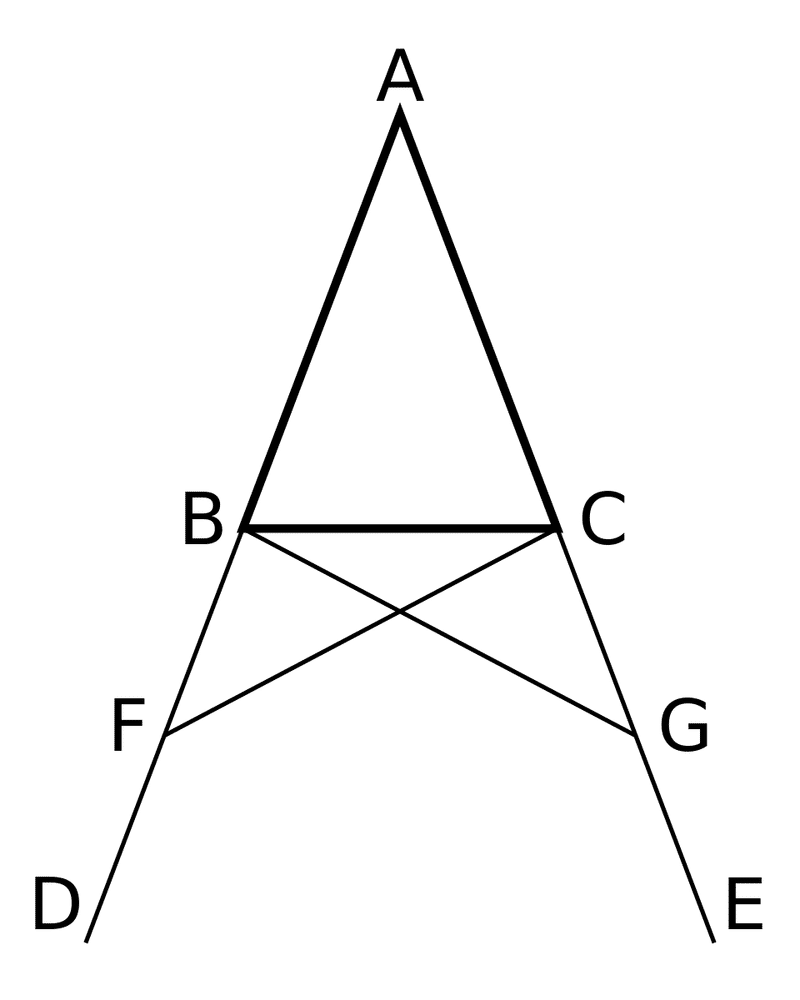
(Wikimedia commons URL: https://commons.wikimedia.org/wiki/File:Euclid_1_5_en.svg)
直観的な明証性を用いて幾何学を構築することは、それはそれで健全で自然なことだろう。古代ギリシャの人たちは、それをわざわざ捨てて、抽象的で目に見えない論理の光による論証を模索し始めたわけだ。そのような明証性に関する大変革の背景には、一体どのような事情があったのか?この問題は古代数学史の謎と言ってもよい、重要な問題である。
この問題に対して、多くの論者がさまざまな議論を展開している。それらの議論は、基本的には
ピタゴラス及びピタゴラス学派の役割
エレア派の哲学、特にエレアのゼノンによるパラドックス
を中心に展開されているようだ。この点に関しては、私も拙著『数学の想像力』(筑摩選書)で、及ばずながら少し書いたことがある。
例えば、ピタゴラスの役割という点では、ピタゴラス学派の教理がそれなりの役割を果たしていると思われる。また、ゼノンのパラドックスがその後のギリシャ数学の展開に及ぼした影響は、決して過小評価できるものではない。
ここから先は

加藤文元の「数学する精神」
このマガジンのタイトルにある「数学する精神」は2007年に私が書いた中公新書のタイトルです。その由来は、マガジン内の記事「このマガジンの名…
この記事が気に入ったらサポートをしてみませんか?
