ソーンダース・マックレーン著『数学-その形式と機能』を読んだ。
本稿はその読書メモである。

概要

いわゆる数学基礎論について、数学全体を俯瞰しながら著者の”機能的形式主義 (functional formalism)”の立場から「数学とは何か？」を記述している、数学の哲学についての書物である。

数学の哲学については他にも書物がたくさんあるが、形式主義を貫きながら基礎論の範囲を超えて数学全体を俯瞰する書物はなかなか無いのではないか。哲学者が書いた書物では、数学と科学の区別がついていないもの・数学と計算規則の区別がついていないもの・そもそも数学が嫌いで数学決別宣言をしているものなどが散見される。一方で数学者が書いた書物では、集合や論理など数学基礎論の範囲に閉じた書物が多いように思われる。
それに対し、本書では数論・幾何学（多様体含む）・関数論・群論とガロア理論・微積分学・線形代数・複素解析と広範にわたり具体的な理論を展開し、共通する形式と機能を見出している。数学のみならず、なんと物理学の解析力学・量子力学にまで及んでいる。各論についての詳細な記述とそれらを俯瞰する形式性は、著者が導く機能的形式主義の立場に大きな説得力を持たせている。

本書は、次の人に勧められると思う。それは、1) 数学の哲学に関心がある人、2) 数学の各専門的なトピックを触りだけさらい深く立ち入らず数学の全体像を得たい人、3) 科学においてなぜ数学がこれほどまでに有用なのか知りたい科学者・科学哲学者、である。一方で、すでに数学の専門家である人には得られるものが少ないように思う。
厳密性は他の書物に譲る方針であり証明は省略される傾向にあるが、アイデアはきちんと記述されており概要を掴むことは難しくない。記述は難しくないが根気は必要だ。なにしろ目次や参考文献・索引を除いても500ページを超えている。予備知識は必要ないと思うが大学1, 2年の教養数学は身につけているのが望ましい。また、圏論 (category theory) を触っているとスムーズに読めると思う。著者は圏論の創始者の一人でもあり、圏論の可換図式 (commutative diagram) が早々に登場するからである。

以降で、各章をかんたんに要約しつつ私の感想を書いてみたい。

序説

本書が解答を与えようとしている問題とはそもそも何であるかが記述されている。それは、「数学の実用的起源および概念的起源は何か、またその発展の性格はどうであるか」ということである。

数学の哲学を論考する上で必ず触れる必要があるのがヴィトゲンシュタインの『数学の基礎』についての講義である。この講義の中でヴィトゲンシュタインはチューリングと議論を戦わせ、哲学者の見方では勝利したということになっている。しかし本書の著者は、ヴィトゲンシュタインを始めとする哲学者が考察の対象にしている数学はせいぜい算術規則程度のものであり、数学の具体例として狭すぎると批判している。その批判がこのような膨大な範囲にわたる数学書につながったのである。

第１章　形式的構造の起源

実際の世界の数、時間、空間、運動について、より詳細を分析するためには形式化された概念が必要であることが、実例を伴って示される。特に、自然界の対称性を形式化するために変換群 (transformation group) などの概念に導かれ、そこからさらに抽象的な群 (group) の概念に至ることが平易に記述されている。運動の概念からは微積分学や連続性の概念が抽出される。連続性の概念の厳密な定式化のために𝜀-𝛿式の定義が出てくる。しかし、連続性の概念は一変数の関数だけでなくどんな空間上でも表現されるべきだろう。しかも連続性の概念は距離の測り方に依存すべきではない（𝜌1という距離で測ったら連続だったが𝜌2という距離で測ったら連続ではなかった、などということはあるべきではない）。著者は、このような内在的な定式化に本書全体を通じてこだわっていることが分かる。「内在的」の原語はおそらく intrinsic と思われるが不明。

この章で導入された概念の詳細を以降の章で分析しながら、数学に内在する形式と構造についてふりかえるという構造になっている。

第２章　整数から有理数へ

数について、ペアノの公準から始めて自然数の集まり𝑵や整数𝒁・有理数𝑸などが構成できることが書かれている。構成する方法は一つには決まらないが、「同形を除いて」一意に決まる。同形とは、一つのモデルから別のモデルへの全単射で公理に現れる述語を保存するものをいう。圏論をかじっていれば、圏論がまさにこの状況を記述するのに便利であることが分かると思う。内在的なものを見抜くためには、同形を同一視する記述が便利なのだ。ちなみにこの章ではまだ圏は出てこない。

第３章　幾何学

幾何学は、ユークリッドの公準に公理を付け加える必要はあるものの、完全な論理的厳密さを持って展開することができる。一方で、「平行線は交わらない」は「『本当』か？」という疑問を巻き起こした。実際は、平行線を交わるものという公理を付け加えて非ユークリッド幾何学（ここでは双曲幾何学）を問題なく展開することができた。これは当時多大な衝撃を持って受け止められたらしい。現実世界はユークリッド幾何学から有意なずれがないように思われたが、非ユークリッド幾何学も内部で矛盾を持たないのであれば、数学的構造を提示しているとは言える。ここに、数学が科学から形式への研究へと変化したことが象徴されている。ひとたび形式化してしまえば、図は必要ない。これが形式化の強みである。

一言で強引にまとめのであれば、幾何学は科学ではないのである。

印象的だったのが、向き付け (orientation) の節だ。回転や面の表裏などは、人為的に向きを決めておく必要がある。このあたりの事情の定式化は煩雑なようで、本書では詳しく述べられていない。しかし、つい最近読んだ田口・西郷の『〈現実〉とは何か』で同じような話題が出てきており印象的だった。

第４章　実数

有理数体𝑸から実数体𝑹をどう構成するか、という話。公理から構成する方法は複数通りあれど、それらは同形を除けば一意的に決まるのである。

i = √-1という数の想定から虚数・複素数という概念が導かれる。これは、数学が科学であるという前提では疑念を持って「想像上の」数であると名付けられた。しかし、もはや数学は科学ではない。複素数を、所定の計算規則に従う数であると受け入れることで数学の視野が広がったことが指摘されている。もちろん、複素数が幾何学の説明に役立ったことも要因である。

第５章　関数、変換および群

この章は面白かったが読み進めるのが難しかった。

まず、関数とは何か？という疑問から始まる。概念としては、関数は「入力に対して出力を対応づける規則」と言っておけば誤った理解にはならない。しかしこれはあいまいである。数学上の概念とするためには、ある公理系の立場で形式的に定義する必要がある。本書では、関数を入力と出力の対の集合として定義している。<𝑥1, 𝑦1>, <𝑥2, 𝑦2>, ...などという具合である。これはおそらく圏論的な定式化なのだと思う。

本章の後半では、群論やガロア理論が概観される。概観といっても5次方程式を冪根で解くことができないことの群論的根拠まで導くのだから、なかなか読み進めるのは大変だった。しかしガロア理論の巧みさや有限群の奥深い構造に驚くことができる、というところまでは到達できたと思う。
圏論における可換図式がここでも出てくる。群の中で一般的な構造を浮かびあがせるのには、圏論が有用なのであろう。

この種の記述で困るのが、対応する英単語がわからないことがしばしばあることである。英語版Wikipediaを参照しながら読むようにした。

第６章　微積分学の諸概念

大学１年生レベルの解析学の復習といったところか。この章は他の章に比べて独立している印象がある。

第７章　線形代数

前半は大学前半レベルの線形代数の復習といったところ。双対空間を記述するにも、基底の選び方に依らない「自然な」同形が選択されるあたり、圏論の創始者らしさを感じる。

後半は群論に関係する内容が多く、読解が難しかった。

第８章　空間が有する形式

曲線や曲面の長さや曲がり具合（曲率）は、内在的なものである。それをどう形式化するかというのが本章のテーマである。

二次元の曲面を、三次元空間に埋め込まれたものとしてではなく、そのものとして内在的に記述する方法がないか。というところから位相 (topology)、チャート、多様体 (manifold)、重なり、リーマン計量などの概念に到達する。

この章はちょっとした多様体の入門章になっている。私は適宜多様体の教科書も参照しながら読み進めた。特に、開集合と閉集合については自分の理解が誤っており、開集合かつ閉集合となりえ、実際にそのような例があることを、本書の読書中に理解した。

リーマン面のはり合わせのところは、だいぶ理解が怪しい。また、前層 (presheaf), 層 (sheaf)の辺りはあまり理解できていない。

第９章　力学

この章は理論物理学よりの話になっている。数学が理論の発展に寄与した部分、また逆に物理の暫定的な理論が数学の発展に寄与した部分が記述される。

主な流れとしては、ケプラーの法則から始まり、ニュートンの法則・座標に依存しないエネルギーなどの物理量の形式化・ラグランジュの方程式・ハミルトンの方程式という解析力学の概観である。

ラグランジュの方程式が座標変換に対して不変であることを圏論的図式で理解しようというのは、本書オリジナルなのではないかと思う。また、ハミルトンの方程式を導くにあたってのアイデアの説明が非常に興味深かった。天下り的にハミルトニアンの定義を与えてラグランジュの方程式からハミルトンの方程式を導出する方が、背景のアイデアを説明するよりはるかに簡単だ。前者は計算して確かめさえすれば良いのだから。著者自身が、ハミルトンの方程式の導出を理解するのに50年以上かかったことを述懐しているのが、それを物語っている。

量子力学やシンプレクティック多様体と力学の関係などは多く述べられていないのが残念だ。

第10章　複素解析とトポロジー

√-1という数から非常に奥の深い数学的構造と他分野との関わりが生まれることの深淵さについて書かれた章。

前半は複素解析の入門として読める。複素関数の径路に沿った積分は、関数が正則であれば、始点と終点のみにより、径路によらない（コーシーの積分定理）。ここから、始点と終点を変えずに径路を変形するホモトピーという概念にたどり着く。そして、視点と終点が同じ𝑧0となる閉じた径路のホモトピー類全体は、ホモトピーの合成操作に対して群をなすのである（ポワンカレの基本群）。ここでも群の構造に導かれた。

収束円を張り合わせて定義域を拡張する解析接続については、その手続きを芽 (germ) と層によって概念的に与えることもできることが記述されている。同じ芽を持つ関数は例によって同値類を構成し、したがって圏論的図式によって見通しよく記述することができる。

この辺りになってくるとこの本だけで理解するのは難しい。複素解析の教科書を参照しながら読み進めた。理解できないところも多々あったが保留とした。学生時代には複素解析の授業で”ホモトピー”など聞いた記憶がなかったが、今複素解析の教科書を見返してみると書いてあったので、おそらく忘れていたのだろうと思う。

正則でない病的関数の一つとして下記が挙げられていた。
𝑓(𝑥) = 𝑥sin(2𝜋/𝑥) (𝑥≠0)
        0 (𝑥=0)
これについて、グラフを描いてみた。

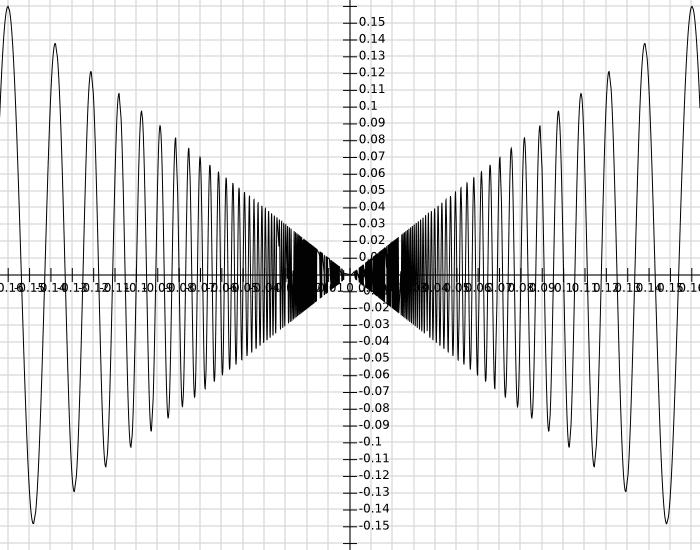
原点に近づくにつれて振動が大きくなり、原点での微分が存在しないことが分かる。しかし𝑥=0でも連続なのである。つまり、どんなに小さな𝜀>0に対しても、ある𝛿>0を取って以下を満たすことができる。
⎮𝑥⎮< 𝛿 となるすべての𝑥について ⎮𝑓(𝑥)⎮ < 𝜀

第11章　集合、論理、圏

数学基礎論についての章で、本書の主題をなすものである。私が本書を手にとった目的は、実はこの章であった。他の章が魅力的だったため、頭からここまで順に読み進めてこれた。

ZFC公理系と命題計算規則、一階の言語によって数学の対象を定式化する、よくある公理的集合論の入門的記述から始まる。これにより、証明が定義できる。そして、この数学の構築に際して、ゲーデルの不完全性定理やコーエンの連続体仮説の独立性の証明などの結果が提出された。これは、結局のところ集合を基礎づける方法が一つではないことを意味する。また、数学を基礎付けるのに集合以外のものを用いた方が良い可能性も示唆していると著者は捉え、圏論に繋がっていく。

圏論については既に他の書籍で触れていたため、この本では流し読みする程度に留めた。記述としては初学者でもついていける内容になっていると思う。

圏論の言葉や図式を用いると、もっとも普遍的なものが何かをうまく浮かび上がらせることができる。同形のものは同一視し、もっとも普遍的な矢印を浮かび上がらせる。積やプルバックなどはその例になっている。

集合論においては冪の存在は非常に重要だが、圏論でももちろん羃を構成することができる。𝑍^𝑌を、𝑌から𝑍への写像の集合と捉えるのだ。
一般に𝑚^𝑛は、𝑛個のものの集合から𝑚個のものの集合への写像の個数と考えられる(𝑚=2の場合は𝑛変数関数の真理値表を書くことと同等になる)。
そして2変数関数𝑓:𝑋×𝑌→𝑍を、𝑥∈𝑋を受け取って「𝑌から𝑍への写像」を返す関数𝐹: 𝑋→𝑍^𝑌に置き換えて考える。これは𝑓から𝐹への推論である。
ここを読んでいた時は、これはまさにプログラミングでのカリー化ではないか！と膝を打ったのであった。
羃の値𝑧∈𝑍は、これを測る関数𝑒:𝑍^𝑌×𝑌→𝑍によって取り出される。つまり、圏論の言葉で言うところの対象(object)𝒁^𝑌と射(morphism)𝑒が羃を定義すると言えるのである。

ZFC公理系に相当する公理系を、圏論の上でも構築できる。これが（非常に粗っぽく言えば）初等トポスである。しかし、真理値集合に相当する対象𝛺を
𝛺={0,1}
で定めれば古典的な論理となるが、二重否定が恒射となるとは限らないので直観主義的な論理になるかもしれない。また𝛺の定義を変えることで、様相論理のような時間によって変化する論理を構成することもできるのである。

著者の『圏論の基礎』は、初学者が読むと挫折することで有名な本だが、この本を読んで概観を掴めばいくばくか敷居が下がるのかもしれない、などと思ったがどうだろうか。

数学の論理について重要な主張が記載されていたので、引用してこの章を締めたい。

厳密さは絶対的なもので、今日の形に定着したものでなければならないということである。もちろん、将来、集合論に対して付加的な公理が付け加わるかもしれないし、集合論に対する別の理論、あるいは、証明を書き留める（または、発見する）ための今日よりも有効な方法が見つかるかもしれない。しかし、厳密な証明が一定の推論規則に従った一連の形式的な手続きであることに変わりがあってはならないのである。

第12章　数学のネットワーク

本書のまとめの章であり、数学の哲学における結論が記載されている。

数学は科学ではなく、したがって現実の世界を描写してはいない。それは形式化された概念と公理、そこから推論規則によって導かれるものの体系である。背景に、現実の世界に類似なアイデアがある可能性はあるものの、それはプラトニズム的な理想化とは一線を画している。

一方で、数学が純粋に形式化されたものなのであれば、なぜ科学にモデルを提供する際に不可解なまでに有効性があるのであろうか？という疑問が残る。これについては、人間が現実をうまく説明する程度に抽象化し形式化することに成功してきた、というしかないだろう。これより踏み込んだ答えを言うには人間の認知能力についての洞察が必要になると示唆され、本書には仮の答えが記載されているにとどまる。

数学の発展についての著者なりの分析も記載されている。本書が書かれたのは1985年であり、フェルマーの大定理も未解決の時である。コンピュータ科学がこれほどまでに発展し、証明をコンピュータによって行い検証する時代になった今でも著者の記述は色あせない。マックレーンが現代のコンピュータ科学の発展を見たらどのように言うだろうか？

まとめ

数学全体を俯瞰しながら数学の哲学について説得力のある結論を引き出す書物は、他に類を見ないと思われる。数学者として結論づけられる限界まで進められた論考だと思う。

数学の入門書としても適しているのではないかと思う。記述はかなり平易で、今季は必要だが難しい知識は必要ない。自分自身、既知の分野は良い復習になり未知の分野は良い入門になったと思っている。ただし、各専門分野の参考書が欲しくなることはたびたびあると思われる。図書館などで読むのが良いだろう。

概念に内在する本質的なものは何か？という問いかけは本書を通じて至る所でなされている。本質的なものをもっともうまく浮かび上がらせる形式を求めて数学が発展してきたのだと理解できる。数理物理学の文脈でも非常におもしろい内容だった。

圏論的記述は、今や数学だけには全く閉じず、物理学・コンピュータ科学他様々な分野で使われている。その背景にある数学的アイデアを同書を通じて吸収すると、日々のものの見方も変わるのではないかと思う。過剰に圏論に当てはめて見てしまうかもしれないが。

「大学においては数学は哲学になる」などと揶揄されることがあるが、形式的な厳密性を追求するとこのようになるということなのだ。本文の言葉を借りれば、

数学は“正確 (correct)”ではあるが“真実 (true)”ではない (p.578)

ということになる。一方で、哲学書はここまで厳密な論考ができているだろうか？哲学も、その観念を数学のように形式的に厳密に定式化し、数学のような厳密な推論規則で展開すべきではないだろうか？私が知る限りでこれを最も試みた哲学者はヴィトゲンシュタイン（前期ヴィトゲンシュタイン）の『論理哲学論考』のみである。数学のようなスタイルの哲学が主流となることを望む。

Reference

ヴィトゲンシュタインの「数学の基礎」についての文献は、例えば以下がある。私はまだ読んでいない。

ヴィトゲンシュタインとチューリングの議論については、下記の書籍が参考にになった。ただし、同書はかなりヴィトゲンシュタインの立場に沿うものであることは念頭におく必要がある。

対称性は物理学において非常に重要である。これはある意味で哲学的な信念とも言えるかもしれない。すなわち、物理法則があるならばそれは座標など人間が決めたものに依らないはずだ、という信念である。このあたりは数理物理学に関係する話であり、新井朝雄先生の『数理物理学の風景』が非常に勉強になる。新井先生も確固とした物理学の哲学をお持ちで、それが同書から読み取れる。数式は出てくるものの非常に平易に書かれており物理学がほとんどわからなくても読める内容だと思う。

田口・西郷の『〈現実〉とは何か』で、人間が向きを恣意的に選択しなければならず、その上に人間の認識が成り立っていることを示唆する記述があった。同書は圏論を用いて物理学と現象学を組み上げており、他に類を見ない書となっている。西郷先生は数理物理学の非可換確率論の専門家であり、圏論の入門書を書いてもいる。

多様体の参考書としては下記を参照した。通読してはいないがかなり平易な教科書だと思う。

複素解析の参考書としては下記を参照した。なお、学生時代に使っていたものではなく社会に出てから購入したものである。

Appendix

ちなみに私の読書時のツイートはこちらからスレッドでぶら下げてある。