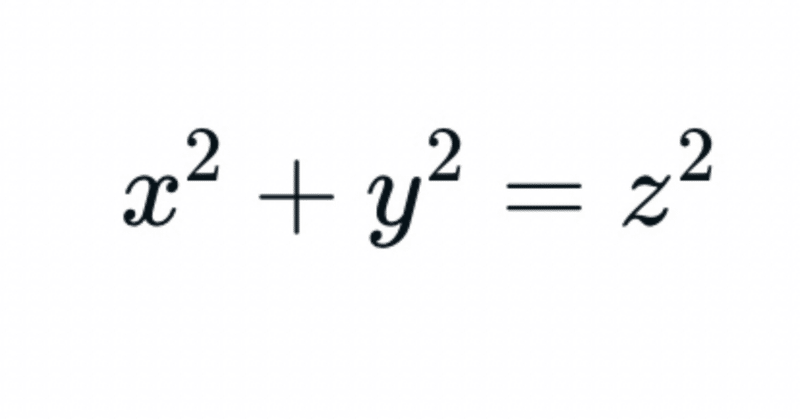
Mathematics short story #3
-------------------------------------------------
$${Published}$$ $${Online}$$ $${First}$$ $${(19/2/2024)}$$
$${Latest}$$ $${additions}$$ $${(19/2/2024)}$$
-------------------------------------------------
数学のどうでもいい小話シリーズ #3
前回で用語の簡単な説明はしたと思います
まず学校で教わる解き方から
結果だけで満足な方は証明をとばして下さい
-------------------------------------------------
【定理1.3】既約(原始)ピタゴラス数
$${\rm(primitive~Pythagorean~triple)}$$
$${x^2+y^2=z^2}$$
の既約な整数解$${(a,b,c)}$$は
$${(a,b,c)=(m^2-n^2,2mn,m^2+n^2)}$$
で表される
$${(m,n)=1}$$つまり$${m,n}$$は互いに素
$${m > n}$$
$${m,n}$$の奇偶は異なる
-------------------------------------------------
まず次の補題を用意します
[補題$${1}$$]
奇数の平方を$${8}$$で割ると$${1}$$余る
[証明]
ある自然数を$${k}$$とし、ある奇数を$${2k+1}$$と表す。
この平方は下記の様になる
$${\begin{aligned}(2k+1)^2&=4k^2+4k+1\\&=4k(k+1)+1 \end{aligned}}$$
このとき$${k(k+1)}$$は連続$${2}$$数の積ゆえ偶数なので、$${4k(k+1)}$$は$${8}$$で割り切れる
ゆえに、$${(2k+1)^2}$$は$${8}$$で割ると$${1}$$余る$${\rm (Q.E.D.)}$$
[補題$${2}$$]
$${x,y}$$は(奇数,偶数)または(偶数,奇数)
の組合せとなる
[証明]
$${x, y}$$が互いに素であると仮定する
$${(i)}$$
どちらも偶数である場合$${x=2m,y=2n}$$$${~(m,n}$$は自然数$${)}$$と表せるので、どちらも$${2}$$で割ることができ互いに素であるという仮定に矛盾
$${(ii)}$$
どちらも奇数である場合
[補題$${1}$$]から、$${x^2+y^2}$$を$${8}$$で割ると$${2}$$余るので$${z}$$も偶数になるが$${z^2}$$は$${4}$$で割り切れるが$${x^2+y^2}$$は$${4}$$で割り切れないので矛盾
$${(i),(ii)}$$から、$${x,y}$$は一方が奇数、 一方が偶数
$${\rm (Q.E.D.)}$$
[補題$${3}$$]
$${2}$$つの互いに素である数の積が平方数のとき、
この$${2}$$数はどちらも平方数でなければならない
[証明]
$${2}$$つの整数の共通の素因数がないことから、$${2}$$つの整数の積が平方数なら、$${2}$$つの整数を素因数分解すると、それぞれの素因数の偶数乗と表せます
よって$${2}$$つの整数は共に平方数となる
$${\rm (Q.E.D.)}$$
-------------------------------------------------
[解法$${1}$$]
[補題$${2}$$]から$${x, y}$$の組の一方が奇数で、もう一方が偶数になるので、$${x}$$を奇数$${y}$$を偶数とすると$${z}$$は奇数となる
ピタゴラス方程式を変形させると
$${y^2=z^2-x^2=(z-x)(z+x)}$$
としたとき$${z-x}$$と$${z+x}$$は、$${x,z}$$が共に奇数だから、共に偶数となる
よって整数$${a,b}$$を用いて
$${z+x=2a,z-x=2b}$$と表すことができる
ゆえに、$${z=a+b, x=a-b}$$となる
この等式から$${a,b}$$が互いに素であることがわかる
なぜならば背理法を用いて、$${a,b}$$が$${1}$$より大きな公約数$${d}$$をもつと$${d}$$は$${x,z}$$の公約数となる
ゆえに$${z+x,z-x}$$も公約数$${d}$$をもつことになるから$${d^2}$$は$${y^2}$$の約数になり、$${d}$$は$${y}$$の約数になる
このとき$${d}$$は$${x,y}$$の公約数となり$${x,y}$$が互いに素であるという仮定に反する
ゆえに$${a,b}$$は互いに素になる
また、自然数$${c}$$を用いて$${y=2c}$$と表すと、$${4c^2=2a・2b}$$
つまり、$${c^2=ab}$$となる
ここで、[補題$${3}$$]から、$${a=m^2,b=n^2}$$と表せる
いま、$${a,b}$$が互いに素なので、$${m,n}$$も互いに素になる
$${x=m^2-n^2, z=m^2+n^2}$$となる
さらに、$${c^2=ab=m^2n^2}$$より
$${y=2c=2mn}$$である
こうして、互いに素な$${m,n}$$を用いて、
$${x,y,z}$$はそれぞれ
$${x=m^2-n^2,y=2mn,z=m^2+n^2}$$
$${\rm (Q.E.D.)}$$
-------------------------------------------------
⭐︎世界一簡単な[解法$${2}$$]はこちらへ
-------------------------------------------------
【まとめ】
ユークリッドの式またはピタゴラスの公式とは、
原始ピタゴラス数$${(a, b, c)}$$は
$${(a,b,c)=(m^2-n^2,2mn,m^2+n^2)}$$または$${(2mn, m^2-n^2, m^2+n^2)}$$
の形のことであり、$${m, n}$$は自然数で、
$${m, n}$$は互いに素
$${m > n}$$
$${m,n}$$の奇偶は異なる
である
次回 #4 ではブラフマグプタの式を説明します
-------------------------------------------------
続きは #4 へ
バックナンバー
#1・#2
最後まで見て頂きありがとうございました😊
-------------------------------------------------
この記事が気に入ったらサポートをしてみませんか?
