D - Shortest Path Queries 2（1190）

問題

問題文

高橋王国には N 個の都市と M 本の道路があります。
都市には 1 から N の番号が、道路には 1 から M の番号が割り振られています。道路 i は都市 Ai から Bi へ向かう一方通行の道で、移動するのに Ci 分かかります。
f (s, t, k) を次のクエリへの答えとして定めます。
・都市 s を出発して都市 t に到着するまでの最短時間を計算してください。ただし、通ってよい都市は s, t および番号が k 以下の都市のみとします。また、都市 t に到着できない場合や s = t である場合におけるクエリの答えは 
0 とします。
全ての s, t, k に対して f (s, t, k) を計算して総和を出力してください。より厳密には、∑_{s=1}^N∑_{t=1}^N∑_{k=1}^N f (s, t, k ) を出力してください。

制約

1 ≤ N ≤ 400
0 ≤ M ≤ N (N−1)
1 ≤ Ai ≤ N ( 1 ≤ i ≤ M )
1 ≤ Bi ≤ N ( 1 ≤ i ≤ M )
Ai ≠ Bi ( 1 ≤ i ≤ M )
1 ≤ Ci ≤ 10^6 ( 1 ≤ i ≤ M )
i ≠ j ならば Ai ≠ Aj または Bi ≠ Bj
である。
入力は全て整数である。

考察　

距離に関するちょっと変なクエリが飛んできますのでそれを処理していきます。

本問題は

ワーシャルフロイド法

という、最短経路を求めるアルゴリズムを用いることで解くことが可能です。と言いますか、ワーシャルフロイド法のアルゴリズムを理解していますか？ということが問われています。ですので、ライブラリをペタリと貼り付けるだけでは、ACが貰えません。裏を返しますと、このアルゴリズムを理解していれば、それだけで正解できます。

ということで、本記事ではワーシャルフロイド法について簡単にですが説明していきます。

まず、ワーシャルフロイド法の前提についてです。このアルゴリズムは

全頂点間の最短経路

を求めることが可能です。ですので、実装に当たっては

各頂点間の距離を管理する2次元配列

を作成することが目標となります。ということで、実際に距離を求めていきましょう。

次の2つのグラフを考えましょう。いきなりですが質問です。このグラフで頂点AからBまでの経路を求めるのはどっちが簡単だと感じますか。

１）

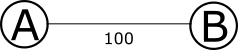
２）

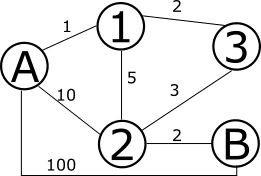
ほとんどの人はグラフ1と答えると思います。最短距離を求める際に難しいのは、考えられる選択肢が多すぎる、ということが原因です。ちょうどそれがグラフ2ですね。それに対してグラフ1はふざけてるのかと思うほど簡単ですね。一目で最短距離が分かります。

グラフ1を少し拡張してみます。

頂点1が増えました。ここで、直接繋がっている辺の距離は分かっているものとします。頂点AとBの距離はこの場合でもまだなんとか求められそうです。直接行く場合と1を経由する場合を比較して小さい方が採用されます。式で表すと次のような感じでしょうか。

最短距離=min((A-B), (A-1-B))

(A-1-B)の１は経由する頂点番号です。ちょっと変形しますと。

最短距離=min((A-B), (A-1)+(1-B))

ですね。このように取りうる選択肢が少なければ一つ一つ比べることでその最短距離がわかるようになります。

また、上記の式は

頂点１を０つ以上経由した際のA-Bの最短距離

と言い換えることができます。少しまどろっこしいですがこの考えが大切になります。

もう一つ頂点を増やしてみましょう。頂点２を追加します。

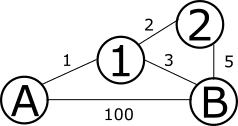
頂点１と同様に次の計算に移りたいのですが、その前にこれまでの計算（頂点１を０個以上経由した際の最短距離）をすべての頂点間に対して行います。ここで経由できるのは頂点１だけであることに注意です。

(A-1-2)
(B-1-2)
(2-1-A)
(2-1-B)

上記の距離は既に計算ができています。

これが計算できたら、頂点２を追加した時の挙動に戻ります。このとき、最短距離となりうるのは

（A-B）
（A-1-B）
（A-2-B）
（A-1-2-B）
（A-2-1-B）

のいずれかです。幸いなことに必要な情報は既に計算できていますので、頂点１の場合と同様に計算しましょう。新しく追加されたのは下３つですね。

最短距離=min(
(A-B),
 (A-2)+(2-B)
 (A-1-2)+(2-B)
 (A-2)+(2-1-B))

これで、頂点1と２が追加された際の最短距離がわかりました。繰り返しとなりますがこれを言い換えますと、

頂点１、２のうち０個以上を経由した際の最短距離

が求まったことになります。ここまで、来ればなんとなく見えて来るのではないでしょうか。これを繰り返していくと、

頂点１、２、３のうち０個以上を経由した際の最短距離
頂点１、２、３、４のうち０個以上を経由した際の最短距離
...

となり最終的には全頂点を考慮したA-Bの最短経路を求めることができます。各段階の遷移を一般化すると次のようになります。

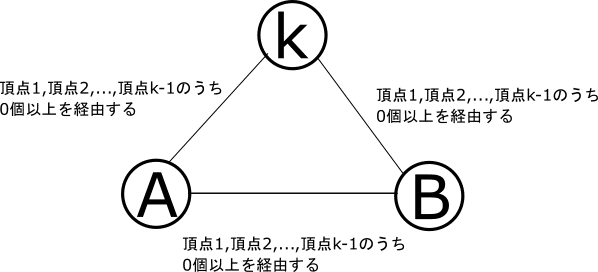
また、その過程ですべての頂点に対して同様の計算を行う必要があるので（２を追加した際に2-1-Aなども求めた）、この計算ですべての頂点間の最短距離を求めることができています。

このように、ワーシャルフロイド法では一番小さなグラフの状態から少しずつ拡張していき最終的に全頂点間の距離を求めることが可能となります。

厳密には各段階ですべての頂点間を計算するので、頂点を追加するという表現は正しくない気がしていますが、小さい状態から順に計算することの説明にこの表現がしっくりきたのでこのように書いています

実装のお話をします。上記の説明では

最短距離=min((A-B), (A-1)+(1-B))

このようにして、最短距離を更新していきます。冒頭にて、ワーシャルフロイドの目的は、各頂点間距離の２次元配列の表を作成することであると述べました。ですので、各頂点間の表の[A][B]の値を計算により更新しましょう。これをすべて計算する頃には表が完成していることでしょう。小さい状態から考えて表を完成させるのってまるで動的計画法（dp）みたいですね。dpと対応付けることで私はすんなりとこのアルゴリズムが理解できました。

最後に具体的な実装です。次のプログラムを書けばこのアルゴリズムは動作します。

//経由する頂点
   for(int k= 0;k<N;++k)
   {
       //始点
       for(int i =0;i<N;++i)
       {
           //終点
           for(int j=0<N;++j)
           {
               dp[i][j] = min(dp[i][j],dp[i][k]+dp[k][j]);
           }
       }
   }

ポイントは経由する頂点がforの外側に来ていることです。説明の通りまずは小さい状態から順に考えているのです。

ここまでくれば本問題は解けたも同然です。本問題では

経由する頂点がk以下の場合の最短距離

を足し合わせます。これってこのアルゴリズムそのものですよね。ということで、各経由点kが終わったタイミングでその時点での距離を足し合わせてましょう。

それを出力すればACがもらえます。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<ll, ll>;
using T = tuple<int, int, int, int>;

int main()
{
   int n, m;
   cin >> n >> m;
   const int INF = 1e9;
   //はじめは全部INFにしておく
   vector<vector<int>> dp(n, vector<int>(n,INF));
   //直接繋がっている部分を更新
   rep(i, m)
   {
       int a, b, c;
       cin >> a >> b >> c;
       --a, --b;
       dp[a][b] = c;
   }
   //1->1みたいな同じ頂点の距離は０となる。
   rep(i, n) dp[i][i] = 0;
   ll ans = 0;
   rep(k,n)
   {
       rep(i, n)rep(j, n)
       {
           dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
           //まだ繋がっていない場合にはINFが書かれてるので足さない
           if (dp[i][j] == INF) continue;
           ans += dp[i][j];
       }
   }
   cout << ans << endl;
   return 0;
}

あとがき

ワーシャルフロイド法の問題でした。いってしまえばアルゴリズムを書くだけなのですが、どうしてそのアルゴリズムで解けるのか、このアルゴリズムは何をやっているのかを考えさせられる良い問題だったと思います。私も大変勉強になりました。

本記事の説明はPAST本を参考にさせてもらっていますが、本説明では私が理解できた噛み砕き方や感覚のようなものを織り交ぜていますので、理解しにくい方もいるかと思います。そのような方はぜひPAST本を購入してみてください。