E - Shiritori（2153）

問題

問題文

高橋辞書には N 個の単語が載っており、i ( 1 ≤ i ≤ N ) 番目の単語は si
です。高橋君と青木君は高橋辞書を使って 3 しりとりをします。 3 しりとりのルールは以下です。
・高橋君と青木君は、高橋君から始めて交互に単語を言い合っていく。
・各プレーヤーは前の人が言った単語の最後の 3 文字で始まる単語を言わなければならない。例えば、前の人が Takahashi と言った場合、次の人は ship、shield などを言うことができ、Aoki、sing、his などを言うことはできない。
・大文字と小文字は区別される。例えば、Takahashi のあとに ShIp を言うことはできない。
・言う単語がなくなった方が負ける。
・高橋辞書に載っていない単語を言うことはできない。
・同じ単語は何度でも使ってよい。
各 i ( 1 ≤ i ≤ N ) について、高橋君が 3 しりとりを単語 si ( 1 ≤ i ≤ N ) について、高橋君が 3 しりとりを単語 sから始めたときどちらが勝つかを判定してください。ただし、二人とも最善に行動するとします。具体的には、自分が負けないことを最優先し、その次に相手を負かすことを優先します。

制約

N は 1 以上 2×10^5 以下の整数
si は英小文字と英大文字のみからなる長さ 3 以上 8 以下の文字列

考察

ちょっと特殊なしりとりをしていきます。問題文を見てどうやって考えるかその一歩目に悩んでしまうかもしれません。

まずは、このゲームをグラフにして考えましょう。グラフの頂点は３文字の文字列になり、問題文に与えられた文字列間に辺を張りましょう。具体例を見ます。

まず、各頂点は「aaa」「aab」「aac」...「aaA」...「aaZ」「aba」,,,「ZZY」「ZZZ」このようになっています。その種類数は、３文字ある各文字に(26*2)種類のアルファベットが入りますので、52^3になります。これは1.4*10^5程度になりますので、O( N )程度の探索なら可能ですね。

次に辺です。「Takahashi」を使って辺を張ります。まず、各頂点には文字が書かれているのですが、この文字は「自分がこの文字から開始しなければいけない３文字」を表しています。ですので、「Takahashi」が使えるのは自分が「Tak」という頂点にいる時だけです。ということで、辺の始点は「Tak」になります。あなたが「Takahashi」を言ったとき、次の人は「shi」から始まる単語をいう必要があります。これは先ほどの「Tak」と同じ状況ですね。ですので、頂点「shi」にいるということです。以上より「Takahashi」がある場合には「Tak」から「shi」に有向辺を貼ってあげましょう。

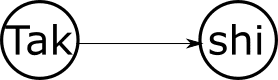
入力で与えられる全ての単語に関して、上記の有効辺を貼ることができれば無事にグラフの完成です。

以上で、問題文からグラフを構築する段階はおしまいです。次はこのグラフ上で「勝ち」「負け」「引き分け」を判定していきましょう。

次にような有向グラフを考えます。

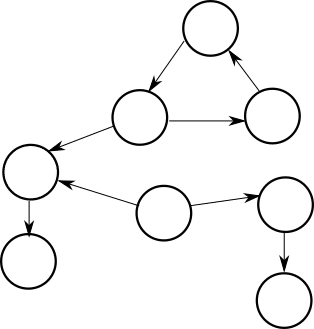
ここでゲーム問題の大切な考え方を使います。

後ろから考える

これをしてみましょう。このゲームの後ろというのは「しりとりにていう言葉がなくなる」ことです。このグラフでいいますと「どこの頂点にも遷移できない頂点」ということになります。

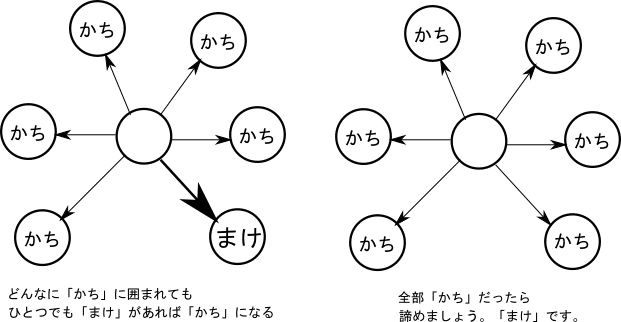
ですので、まず移動することができない頂点を「負け」としましょう。この頂点にいる時に手番が回ってきてしまったら文字通り負けとなる頂点です。

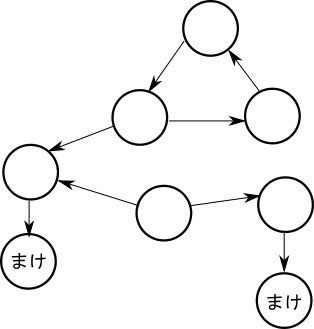
続きまして、負けに遷移できる頂点を考えます。もし自分の手番の時に遷移できる頂点の中に「一つでも」負けの頂点があればその頂点は勝ちになります。これは相手に負けの状態を渡すことができるからですね。この辺りの考え方が、問題文に与えられている「相手を負かすことを優先します」という点につながります。

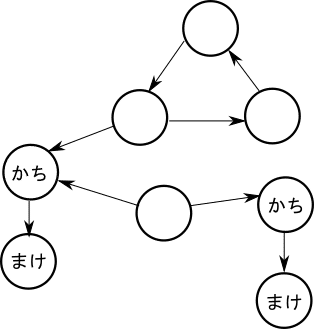
次に、勝ちに遷移できる頂点を考えます。この場合は負けの場合とは異なり「一つでも」勝ちの頂点があったら負け、ということにはなりません。勝ちの頂点があっても、その頂点に遷移しなければいいのです。その頂点にいるのはあなたで好きな選択肢を選ぶことが可能なのですからね。

ただし、移動できる頂点が全て勝ちの場合には話が変わってきます。どんなに良い頂点を選ぼうとしても、敗北しか待ち受けていません。四面楚歌ってやつです。このように遷移できる「全て」の頂点が「勝ち」となってしまったら、その頂点は負けとなります。

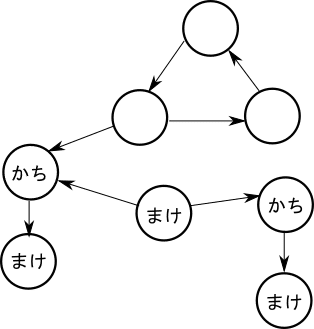
上記の操作をしていくとこで、どんどんグラフが埋まっていきます。ただし、全ての頂点が決定されるわけではないです。例のグラフでも空欄のままの頂点があります。これらの頂点は「引き分け」となります。

これがなんでこれが引き分けになるの？

と考える方もいると思います。そんな方は、あとがきで紹介している記事にて詳しく解説されていますのでそちらを見ていただけると助かります。

本記事でも簡単に説明をします。次の頂点にいると考えます。「ココ」ってやつです。

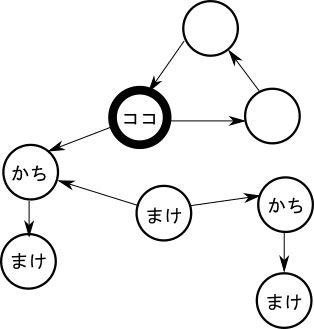
この頂点から下にいけば、ループを回避することができますが、次の頂点は「勝ち」の頂点です。ですので、相手に勝ちを渡してしまって、自分は「負け」てしまいます。ということで、それは嫌なので、一旦は勝ちも負けもしない右に移動してお茶を濁します。ループ長は奇数なので、次にこの頂点に来るのは、別の人になります。しかし、状況は同じです。その人も負けたくありません。ですので、また右に行ってお茶を濁します。

ということを繰り返していくと永遠に勝負がつきません。ということで「ひきわけ」になるわけです。今回はループ長が奇数でしたが、これが偶数でも同じです。この頂点が同じ人に巡って来るだけです。この点が「自分が負けないことを最優先」になります。

以上の遷移のイメージはこんな感じです。

これをプログラムで実装してあげれば答えが求まります。実装の工夫を２点説明します。

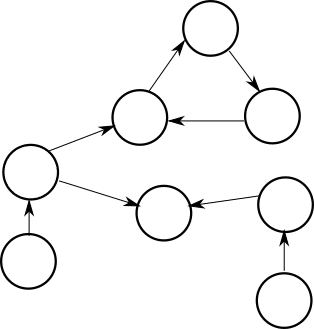
１点目です。グラフ上で考えるときは、「負けの頂点に遷移できる頂点」みたいなことをやっていました。これをプログラム上でやりたいので、冒頭で説明した辺を逆向きに張ります。「Takahashi」なら「Tak」から「shi」ではなく、「shi」から「Tak」に辺を張ります。これで、後ろから考えることが可能になります。上のグラフですと逆向きはこんな感じです。

２点目です。上記の操作を愚直に実装してあげるとO( N^2 )の計算時間がかかります。ですが、制約をみるとこれでは間に合いません。工夫しましょう。まず、

・各頂点において遷移できる頂点の個数

を管理してあげましょう。いわば、各頂点の選択肢の数ですね。この個数がわかれば、まずは負けの頂点が判明します。この値が０の頂点です。もう遷移のしようがありません。ですので、遷移できる頂点数が０個の頂点に「負け」を書き込みましょう。「負け」「勝ち」が決まった頂点とつながっている頂点を考えていくため、queueを用意して、この頂点を詰めていきます。

次にこの負けの頂点から（逆向きのグラフで）遷移できる頂点を考えていきます。実装の際には、queueに入っている、頂点を一つ取り出してくればOKです。負けの頂点に遷移できる頂点は「勝ち」の頂点になります。ですので、その頂点に「勝ち」を書き込みます。「勝ち」が決まったので、この頂点もqueueに詰めていきます。

続きまして、その「勝ち」の頂点から遷移できる頂点を考えます。「勝ち」の頂点から（逆向きのグラフで）遷移できる頂点だからと言って、すぐに負けと決まるわけではありません。ただし、その頂点の選択肢の数は一つ減ってしまったわけです。まだ、確定はしていませんが、頂点数を−１しましょう。この値がその頂点の残機となり、これが０となったら「負け」が確定します。「負け」が確定した時点でその頂点をqueueに詰めます。−１しただけでは詰める必要はありません。未確定の頂点からは何も絞れることがありません。

このような遷移を繰り返し行って、「勝ち」「負け」を断定できなくなったら探索終了です。決まらなかった頂点は「引き分け」です。探索の終了はqueueが空になることで判断ができます。

上記の探索を行えば、各頂点の「勝ち」「負け」「引き分け」がわかります。あとは、全ての単語についてその頂点の状態からどちらが勝つかを出力してあげればACがもらえます。

実装の細かいところはコメントにて補足します。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int,int>;
using T = tuple<int, int, int>;
//文字列を数字に変換する
int s2i(string s)
{
   int res = 0;
   for(auto c:s)
   {
       res *= 52;
       int now = c-'a';
       if(now<0) now += 58;
       res += now;
   }
   return res;
}

const int M = 52*52*52;
int main()
{
   int n;
   cin >> n;
   vector<string> s(n);
   rep(i,n) cin >> s[i];
   vector<vector<int>> g(M);
   //同じ辺を張らないように管理する
   map<P,int> mp;
   //その頂点から出ている辺の本数
   vector<int> deg(M,0);
   rep(i,n)
   {
       int a = s2i(s[i].substr(0,3));
       int b = s2i(s[i].substr(s[i].size()-3));
       if(mp[make_pair(a,b)]) continue;
       ++mp[make_pair(a,b)];
       //通常はa->bに遷移可能
       //逆辺なのでb->aの辺を貼る
       g[b].emplace_back(a);
       ++deg[a];
   }
   queue<int> q;
   vector<int> ans(M,-1);
   rep(i,M)
   {
       if(deg[i] == 0) 
       {
           q.emplace(i);
           ans[i] = 0;
       }
   }
   while(!q.empty())
   {
       int v = q.front();
       q.pop();
       if(ans[v] == 0)
       {
           for(auto nv:g[v])
           {
               //もう既に勝ちが決定していたら計算しない
               if(ans[nv] == 1) continue;
               ans[nv] = 1;
               q.emplace(nv);
           }
       }
       else
       {
           for(auto nv:g[v])
           {
               //勝ちが決まっている頂点には計算しない
               if(ans[nv] == 1)continue;
               --deg[nv];
               if(deg[nv] == 0)
               {
                   ans[nv] = 0;
                   q.emplace(nv);
               }
           }
       }
   }

   for(auto si:s)
   {
       int num = s2i(si.substr(si.size()-3));
       if(ans[num] == 0) cout << "Takahashi" << endl;
       else if(ans[num] == 1) cout << "Aoki" << endl;
       else cout << "Draw" << endl;
   }

   return 0;
}

あとがき

本問題のようにグラフ上の各状態の勝ち負けを考えていくことを

後退解析

というみたいです（厳密な定義はわかりません）。これは本問題みたいに状態がループするような問題も扱うことが可能となります。このアルゴリズムを使えば「どうぶつしょうぎ」で最強になれるらしいので、張り切って学んで見てはいかがでしょうか。

また、考察において、私が参考にさせていただいた記事となります。非常に詳しくかつ分かりやすく書かれていますので、一度読んでみるとさらに良いことがあると思います。