F - Cumulative Sum（2772）

問題

問題文

非負整数 n, mに対して関数 
f(n,m) を正の整数 Kを用いて次のように定めます。
f(n, m)
= 0 (n=0)
  n^k (n>0,m=0)
 f(n-1,m)+f(n,m-1) (n>0,m>0)
N, M, K が与えられるので、
f(N, M) を (10^9+7)で割った余りを求めてください。

制約

0 ≤ N ≤ 10^18
0 ≤ M ≤ 30
1 ≤ K ≤ 2.5×10^6
入力は全て整数である。

考察

本記事では「ラグランジュ補間」を用いて本問題を考えていきますが、その詳細な解説や証明には触れません（大変ですので、、、）。本記事では、本問題をACすることができる最低限の説明をしていきます。

そのため、「何をする問題なのか」「どんな感じで解いていくのか」などの概要や全体像を掴む際にはお役に立てると思います。一方で、踏み込んだ話はしていませんので、そちらは公式解説や後ほど紹介する記事にお任せしようと思います。

本記事は次のような構成で書いていきます。

１）何をする問題なのか
２）ラグランジュ補間の簡単な説明
３）f(N+M)がM+K次になる簡単な説明
４）ラグランジュ補間と本問題の対応
５）実装の注意点

ではいきます。

１）何をする問題なのか

まず、なにを求めればいいかを説明してきます。制約などを考えずに、NとMが小さい場合の表を実際に作ってみましょう。このときK=2としておきましょう。

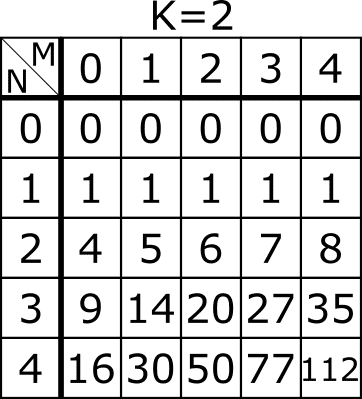
この表はYoutubeの公式放送と同じです。ここで、入力がN=4,M=3としてみましょう。このとき、上の表から

f(4,3) = 77

とわかります。本問題は様々なN,M,Kに対してこの値を求めるという問題です。問題の設定は非常にシンプルだと思います。

ただし、本問題の制約に注目しますと。N<=10^18と非常に大きくなっています。小さい方から表を埋めていくと、N*M回の計算が必要になります。これは流石に間に合わないです。

ですので、２）以降ではこのf(N,M)を高速に求めるために色々と工夫をしていきます。その手法がラグランジュ補間というわけです。

２）ラグランジュ補間の簡単な説明

ラグランジュ補間の説明をしますので、一旦、１）での説明は忘れてください。４）で対応させます。

ラグランジュ補間の前にちょっと中学生の数学に戻ります。

y = ax + b

という式があります。1次関数ですね。このとき（x, y）の情報がいくつあれば(a, b)を求めることができますか？言い方を変えますと、

xy平面上に直線（一次関数）を引きたいです。この情報だけだと無限に直線が引けててしまいます。でも、「ある点を通ってください」という条件が与えられるとだんだん直線が限られてきますね。では、いくつの条件（通る点）が与えられたときに直線はただ一つに定まりますか？

という感じですね。早速結論なのですが、この場合には２点あれば直線が唯一に定まります。まあそうなんですけども、この性質がとっても大事になります。

先ほどは１次関数でしたが、2次関数の場合には３点必要になります
3次関数では4本です。

ということで、一般に次のことがわかります。

N次関数はN+1個の点があれば求めることが可能

厳密な表現でもないし唯一性の証明なんかも省きますが、これがとっても大切なんです。この「N+1個の点からN次関数を求める」ことを一般化したのが本節のテーマとなっている「ラグランジュ補間」で、次の式で表されます。

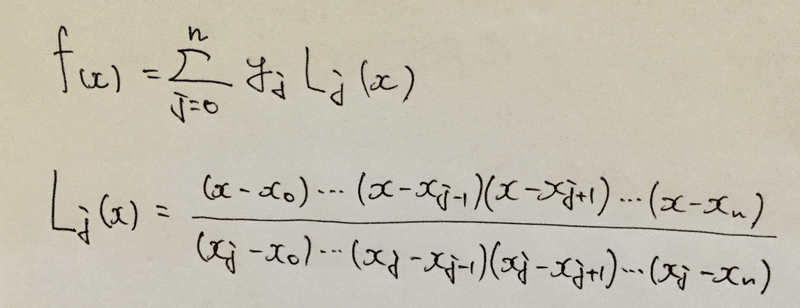
証明は本記事末尾で紹介している記事を参考にしていただきたいです。また、これだけだといまいちパッとしませんが2次関数なんかで実際に計算をしてくれていますので一度覗いてみると良いと思います。

３）f(N+M)がM+K次になる簡単な説明

先に結論です。

今回求めたいf(N, M)は M+K 次式で表されます。

ということは２）の性質より、 M+K+1点がわかればf(N, M)が求められてしまうわけです。不思議ですね。制約の中でネックとなっていた N を使いませんので、この方法でなら計算が間に合いそうです。

この節の説明は公式解説 2.3.4. で説明されていますので、ここではその補足と言いますか、私が理解に苦労した点を説明します。

まず、全体を通しまして、表の各マスの値f(.)と縦列の総和S(.)を勘違いしないように注意しましょう。私はこの点で非常に時間を使いました。

M=0 のときから始めましょう。問題文よりこの時の各マスf(n, 0)の値は n^K となります。これはもちろんK次式ですね。また、M=0のときの縦列の総和S(n, 0)はK+1次式で表されます。ここまでが、公式解説2. 3.までの内容です。

一つ横の列に移りましょう。m=1です。このとき、f(n, 1)はK+1次でS(n, 1)はK+2次で表されます。という説明が公式解説4.でされています。なんかそうなるみたいです。

これを繰り返していくとf(n, M)はK+M次式ということがわかります。

ほとんど説明していませんが、f(n, M)はK+M次式ということだけわかれば十分です（少なくとも本問題を解くだけであれば）。

４）ラグランジュ補間と本問題の対応

１）２）３）において確認したことをおさらいしましょう。

・f(N, M)を高速に求めるという問題である
・N次式はN+1点あれば求められる
・ラグランジュ補間を使うと簡単に求められる
・f(N, M)はK+M次式

です。

これを踏まえて本問題の全体図を次に示します。

M+K+1点は(0, f(0,M)), (1, f(1,M)), ... , (d, f(d, M))が対応します。

ここで、L(0,M),L(1,M),...,には似たような部分が出現していますね。この部分は工夫しながら高速化が必要です。詳しくは５）で説明します。

あとは必要な情報を一番上の式に詰め込んで行けば答えが求まります。こうしてみると理論こそは難しいもののやることは結構単純なのではないでしょうか。

５）実装の注意点

あとは４）の通りに計算するだけなのですが、この実装には私は２時間かかりました。つまづいた点を説明していきます。

・Lの分子
L(i, M)の分子の値は i の値に関係なくそのほとんどが一定です。ですので、N-0からN-dまでの積をもとめてL(i, M)のときに(N - i)で割れば一発で計算できます。と思っていました。ただ、これ入力例３でうまくいきません。その理由は、本問題は10^9+7で割った値を出力するからです。計算をしていくと、i = 50付近でその積が 10^9+7 で割り切れてしまいます（というよりかはN-iが10^9+7の倍数になります）。一度、割り切れてしまうと剰余が0となってしまいます。あとから、その値を取り除こうと(N-i)で割ったところで復元できません。ですので、少し大変ですが、左右からの累積積で計算しましょう。

・Lの分母
一般化すると

i ! * (-1)^{d-i} * (d-i)!

なんですが、このまま実装すると、(-1)^{d-i}を毎回計算する必要があります。繰り返し２情報でlogがつくとしても流石に間に合いません。今回必要なのは正負、d-iの偶奇だけですので、おとなしくif分で場合分けしましょう。

これらの高速化は本問題の各 x が0,1,2,3, ... と連続であるため可能となっています。一般のラグランジュ補間ではできませんのでその点注意です。　

・少数
特に説明もなくLの分母として割り算をしています。でもmodintのライブライを作っておけばこれで問題ありません。勝手に逆元の計算をしてくれています。もしライブラリがなかったらmod-2乗で計算しましょう。フェルマーの小定理というやつです。

説明は以上でおしまいです。あとはコメントにて補足しています。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
using T = tuple<int, int, int>;

const int mod = 1e9 + 7;

class mint
{
public:
   long long x;
   mint(long long x = 0) :x((x% mod + mod) % mod) {}
   mint operator -() const { return mint(-x); }
   mint& operator +=(const mint a)
   {
       if ((x += a.x) >= mod) x -= mod;
       return *this;
   }
   mint& operator -=(const mint a)
   {
       if ((x += -a.x + mod) >= mod) x -= mod;
       return *this;
   }
   mint& operator *=(const mint a)
   {
       (x *= a.x) %= mod;
       return *this;
   }
   mint operator+(const mint a)
   {
       mint res(*this);
       return res += a;
   }
   mint operator-(const mint a)
   {
       mint res(*this);
       return res -= a;
   }
   mint operator*(const mint a)
   {
       mint res(*this);
       return res *= a;
   }
   mint pow(long long t) const
   {
       if (!t) return 1;
       mint a = pow(t >> 1);
       a *= a;
       if (t & 1) a *= *this;
       return a;
   }
   //for only prime number
   //Fermat's little theorem
   mint inv() const
   {
       return pow(mod - 2);
   }
   mint& operator/=(const mint a)
   {
       return (*this) *= a.inv();
   }
   mint operator/(const mint a)
   {
       mint res(*this);
       return res /= a;
   }
};


int main()
{
   ll n, m, k;
   cin >> n >> m >> k;
   int d = m + k;
   //まず愚直な計算でd*mの表を埋める
   vector<vector<mint>> table(d + 1, vector<mint>(m + 1));
   //繰り返し2乗法にて高速に計算
   rep(i, d + 1) table[i][0] = mint(i).pow(k);
   reps(i, 1, d + 1)reps(j, 1, m + 1)
   {
       table[i][j] = table[i - 1][j] + table[i][j - 1];
   }

   //n<=dなら表から答えを出力して終了する
   if (n <= d)
   {
       cout << table[n][m].x << endl;
       return 0;
   }
   //ラグランジュ補間の分子
   //左右からの累積積
   vector<mint> mol_l(d + 2), mol_r(d + 2);
   mol_l[0] = 1;
   mol_r[d + 1] = 1;
   rep(i, d + 1)
   {
       mol_l[i + 1] = mol_l[i] * mint(n - i);
       mol_r[d - i] = mol_r[d - i + 1] * mint(n - (d - i));
   }

   //分母
   //dまでの各値の！を求めておく
   vector<mint> den(d + 1);
   den[0] = 1;
   rep(i, d) den[i + 1] = den[i] * (i + 1);

   //ラグランジュ補間の各項の計算
   mint ans = 0;
   rep(i, d + 1)
   {
       mint Li = mol_l[i] * mol_r[i + 1];
       Li /= den[i] *  den[d - i];
       if ((d - i) % 2 == 0) ans += table[i][m] * Li;
       else ans -= table[i][m] * Li;
   }
   cout << ans.x << endl;
   return 0;
}

あとがき

上記コードの計算時間は1878 msです。ギリギリでした。一応、一番初めの表を求める部分で配列を使いまわすことで1331msまで高速化をしています。そちらのコードはgithubにてあげてますのでもしよければご覧ください。

ただ、C++でこれだけかかっていますので、他の言語だと厳しいのかもしれません。高速化できそうな部分があったらお知らせいただけると嬉しいです。

また、本記事は問題をACするだけの最低限の説明にとどめています。詳細な説明は次のサイトにてご確認いただければと思います。ACできた後は、証明にも目を通しておくと良いと思います。