D - National Railway（1507）

問題

問題文

高橋王国は H 行 W 列のグリッドで表されます。北から i 行目、西から
j 列目のマスを(i, j)で表します。
このたび、高橋王国の国民から交通の利便性のために鉄道の建設を求める声が多数寄せられ、国王の高橋君は鉄道を建設しなければならなくなりました。
鉄道建設は以下の 2 つのステップからなります。
まず、2 つの異なるマスを選び、それぞれに駅を建設する。マス (i, j) に駅を建設すると Ai, j 円の費用がかかる。
その後、建設した 2 つの駅を結ぶ線路を建設する。2 つの駅がマス(i, j)とマス
( i′, j′ ) にあるとき、これらを結ぶ線路の建設をすると C×(|i−i′|+|j−j′|)円の費用がかかる。（ここで、|x|は x の絶対値を表す。）
高橋君は国民の利便性を上げることよりも、鉄道建設にかかる費用を少なく抑えることを優先したいと考えています。
鉄道建設にかかる費用として考えられる最小値を出力してください。

制約

2 ≤ H, W ≤ 1000
1 ≤ C ≤ 10^9
1 ≤ Aij ≤ 10^9
入力はすべて整数

考察

マンハッタン距離に関わるスコアとそのマスに与えられた建設費の和の最小値を求める問題です。

まず、制約をみますと、グリッドの1辺は10^3ですので、最大マス数は10^6になります。ですので、駅１と駅２の組み合わせを全探索するといったようなO(N^2)の解法では間に合いません。

計算量の改善を考えていきます。ここで問題となるのが

「距離が近い」ことを優先するべきなのか「建設費が小さい」ことを優先すべきなのか

ということです。あちらを立てればこちらが立たないといった設定になっています。今回は、駅１と駅２に条件を設けることによりスコアの式を変形して解いていきます。問題文から与えられるスコアの式は次のようになります。

Aij + Ai'j' + C×(|i−i′|+|j−j′|)

ここで、(i, j)は駅１の座標、(i', j')は駅２の座標です。ここで、駅１は駅２よりも右下にあるという条件を勝手に設けます。式で表しますと次の通りです。

i' ≦ i かつ j' ≦ j

こうしますと、嬉しいことにスコアの式の絶対値が外れますので、次のように変形できます。

Aij + C * (i+j) + Ai'j' - C * (I'+j')

ここで、この式の前半部（１,２項）は駅１、後半部（3,4）項は駅２に関する高となっています。

この式を用いて問題を考えます。説明のために

X = Aij + C * (i+j)
Y = Ai'j' - C * (I'+j')

としておきます。このXとYはそれぞれ独立しています。そのマスと他のマスにより算出されるということはなく、そのマスの情報だけで計算されるということです。また、各マスはXとYの両方の値を保持しています。

とすると、この問題は

Xから１つ、Yから１つ選んだ時の値の最小値を求める問題

と言い換えることができます。この時点でマンハッタン距離とかは登場しなくなりますね。説明が駆け足になってしまったので具体例を示します。次のような状態を考えます。

この表の各X,Yは次のようになります。

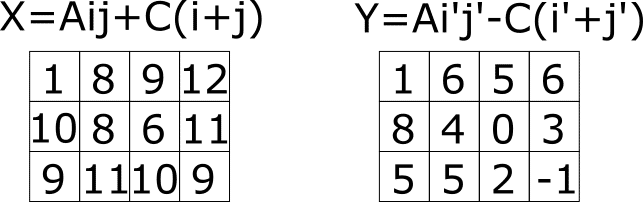
この２つの図の左から１つ、右から１つ値を選んだ時、その和の最小値を答える問題となります。ただし、勝手に制約をつけましたので、Xの場所によって、Yで選ぶことのできる範囲が変わってきます。

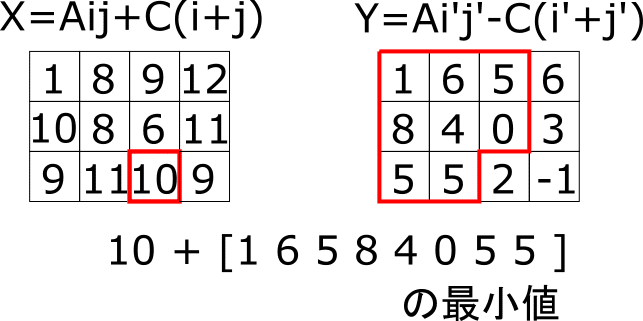
Yではこの範囲内での最小値を採用してあげれば良いのですが、これを一つずつ調べてしまうと時間が足りません。もう少しだけ工夫します。

Yの図を工夫します。Yの値を各マスよりも左上にあるマスの最小値としてあげましょう。こうすることで、Xを選んだ時、そのマスの上と左を見るだけで、選択可能なYの最小値を求めることができます。

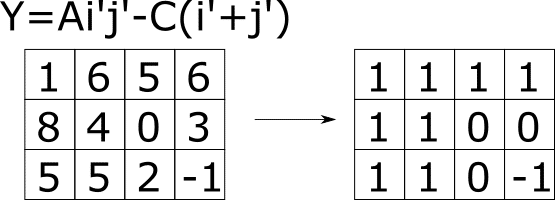
左上に１があってあんまり面白くはないですね。でも、このようにしておくことで、次のように一発で値を求めることが可能です。

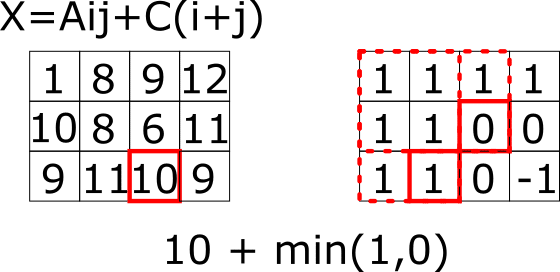
これをすべてのXに対して行います。

ただし、今回は

i' ≦ i かつ j' ≦ j

を勝手につけていましたね。ですので、Xより右上にあるYを選ぶことができませんので、これでは全ての組み合わせを調べたことにはなりません。ですので、値の表を上下反転して同じことをもう一度行います。こうすることで、全ての組み合わせに対して計算を行うことができました。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
using T = tuple<int, int, int>;

int main()
{
	int h, w;
	ll c;
	cin >> h >> w >> c;
	vector<vector<int>> a(h, vector<int> (w));
	rep(i, h)rep(j, w) cin >> a[i][j];
	const ll INF = 1e18;
	ll ans = INF;
	rep(i, 2)
	{
		vector<vector<ll>> dp(h, vector<ll>(w,INF));
		rep(hi, h)rep(wi, w)
		{
			ll now = INF;
            //nowにはYの値を入れる
			if (hi > 0) now = min(now, dp[hi - 1][wi]);
			if (wi > 0) now = min(now, dp[hi][wi - 1]);
            //X = a[hi][wi]+c*(hi*wi)
            ans = min(ans, a[hi][wi]+c*(hi+wi)+now);
			dp[hi][wi] = min(now,a[hi][wi]-c*(hi+wi));
		}
        //上下反転
     	reverse(a.begin(), a.end());
	}
	cout << ans << endl;


}

あとがき

実装では、最小値を更新しながら表を埋めていきましたが、まず表を埋めてから一つずつ計算を行っても十分間に合います。ですので、なんか実装できないな、となった方は、一つずつ処理していくと良いと思います。

マンハッタン距離に制約を加えて独立して解くこの方法すごいですね。公式放送の解説を聞いていて感動しました。マンハッタン距離といえば45度回転みたいな、単純な覚え方をしていましたが、絶対値を外して各要素ごとに考えられることが重要なんですね。とっても学びの多い問題でした。