E - Digit Products（2024）

問題

問題文

N 以下の正の整数のうち、各桁の数字の積が K 以下であるものは何個ありますか？

制約

1 ≤ N ≤ 10^18
1 ≤ K ≤ 10^9
入力は全て整数である。

考察　

桁DPをやりましょう。というメッセージが伝わってきますので、それに従います。桁DPを考えていきます。

今回は最も工夫をしない単純な3次元dpにて解いていきます。dpの構成は次の通りです。

dp[ i ] [ j ][ t ]:
上から i 桁目にて
現在の各桁の積が t であり、
もし、現在の桁まで N の と一致していたら
 j=1していなかったら、 j = 0

です。入力のKと被るので t を使っています。

解けた後に見直してみると結構無駄の多い構成となっていますが、そのくらいの方が理解しやすかったりするので、とりあえずはこれで考えます。計算時間も十分に間に合いますので大丈夫です。

ここで、制約に注目します。各桁の積 K は10^9 までありますので、愚直に回すと全然計算が間に合いません。これは困りました。

でも、本問題の構造を考えるとこの制約は全く問題になりません。というよりもむしろ K に合わせてfor文を回してしまいますと正しい答えにたどり着けません。その点に関して説明します。

１）Kの制約が問題にならない理由

本問題にて取りうる t の値について考えていきます。t は各桁の積ですので、1~9は出現しそうですね。先頭の桁を１つ取ってきた場合に各数字の状態は発生します。また、一つでも0を選びますとtは0になりますので、0もありそうです。また、2桁の数字でも2と5を取ってくると10は出現しそうです。

一方で、11や13なんかはどんなに頑張っても発生することはありません。0~9をどんなにうまく組み合わせてもこれらの数を表現することができません。

以上のことより、出現する数（tとしてあり得る値）は

0~9の積で表現できる

ことが条件となります。もう少し狭めますと

0, 1, 2, 3, 5, 7

の掛け算で表現できる数になります。では、これらの掛け算でできる数字はどのくらいあるのでしょうか。

本問題では最大で18桁あります。そのすべてが9だった時の値が取りうる t の最大値となります。ということで計算すると9^18 ≃ 1.5*10^17となるそうです。だいたい、10^18ですね。ですので、上記の数（2,3,5,7）を色々と組み合わせてその積が10^18以下になる数字の組み合わせ数を求めます（0と1を含めると無限通りできますので使いません）。

求めます、と書きましたが、公式放送で既に求めてくれていますのでありがたく使わさせていただきます。放送曰く「66000」程度になるそうです。つまり、各桁において t は 6*10^4 程度しか回りません。最初の10^9からだいぶ少なくなりましたね。この値でしたら、各桁で計算しても、18倍するだけですので十分に間に合いそうです。

実装では出現した数だけを回すためにmapを使用しています。

２）Kまでで回すと正しくない理由

こちらは１）よりは簡単です。１）でも少し触れました。0で掛けると0になってしまうからです。各桁の積がKを超えた時点で計算をやめてしまうと、現在の積が「K+100」でも次の桁で「0」を選ぶから、はいセーフ、みたいな遷移ができなくなってしまいます。

ですので、１）の説明の通り出現した t は捨てずにとっておきましょう。

これで、 t についての説明はおしまいです。あとは通常の桁dpをやるだけななので、上記のdpの構成通りに丁寧に実装してあげれば答えが求まります。

方針としてはN以下の条件は守り、K以下の条件は無視したdpを行って、あとでKの条件を満たしているものをカウントする。

なんですが、実装がなかなかややこしいのでコメントにて補足しています。

実装です。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int,int>;
using T = tuple<int, int, int>;

int main()
{
   ll n, k;
   cin >> n >> k;
   vector<int> d;
   while (n > 0)
   {
       d.emplace_back(n % 10);
       n /= 10;
   }
   int sz = d.size();
   vector<vector<map<ll, ll>>> dp(sz + 5, vector<map<ll, ll>>(2));
   ll x = 1;
   bool first = true;
   rep(i, sz)
   {
       int di = d[sz-i-1];

       //1桁目の処理
       if (first)
       {
           //1桁目はdiまでしか入らない。
           for (int next = 1; next < di; ++next)
           {
               //di以下であればj=0
               dp[i + 1][0][next] += 1;
           }
           //もしdiのときはj=1となる
           dp[i + 1][1][di] += 1;
           x *= di;
           first = false;
           continue;
       }
       //2桁目以降でその桁で初めて0以外の数を追加する
       for(int next = 1;next<10;++next)
       {
           dp[i + 1][0][next] += 1;
       }
      
       //前の桁の時点で小さい
       for (auto [t, val] : dp[i][0])
       {
           rep(next, 10)
           {
               //val = dp[i][0][t]です。autoで定義してます。
               dp[i + 1][0][t * next] += val;
           }
       }
       //前の桁の時点では等しい
       //その時の掛け算は一意に決まる（x）
       //その桁で小さくなる
       rep(next, di)
       {
           dp[i + 1][0][x * next] += dp[i][1][x];
       }
       //その桁でも同じ
       dp[i + 1][1][x * di] += dp[i][1][x];
       //その桁までの積を保持しておく（j=1の条件）
       x *= di;
   }
   //最終桁まで計算後、kの条件を見たいしているものをカウントする
   //Nの条件はdp時に考慮している
   ll ans = 0;
   for (auto [t, val] : dp[sz][0])
   {
       if (t <= k) ans += val;
   }
   if (x <= k) ++ans;
   cout << ans << endl;
   return 0;
}

あとがき

補足です。まず桁dpについてです。完全にイメージの話なのですが私は桁dpがわからないときに次の図を書いたら非常にすんなりと理解できました。問題によって細かなところは異なりますが、本問題はこんな感じになると思います。

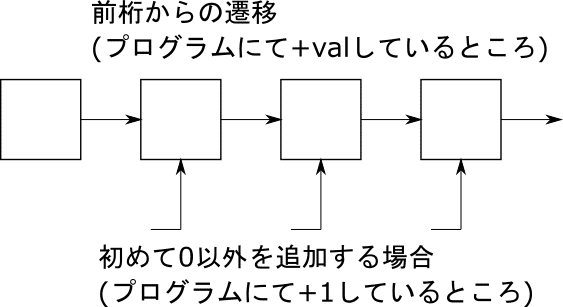
これに、j=1とかの条件を加えてあげればdp遷移が書けると思います。

つぎに j についてです。状態を考えてみますと、j = 1になるのは i 桁目までが N とすべて等しい場合です。ということは、その時の t の値って１つに決まってしまいますね。N の i 桁目までの積です。

ですので、 t = Π_{0}^{i} di （プログラムでは x です）をj=1の状態とみなすことができますので、j を情報として保持しておく必要はなくなります。

また、循環参照を避けるために一度仮の配列を用意してあげれば i の情報も必要なくなります。これは、インラインdp、配列の使いまわし、実家dpと呼ばれるやつです。

公式放送では上記２点を用いて、1つのmapで実装しています。これ本当に賢いですよね。初めて見たときは何事かと思いました。

3次元実装ができたら、ぜひ次元削減に挑戦してみてはいかがでしょうか。