F - Deforestation（2307）

問題

問題文

N 本の木が左右一列に並んでおり、左から i ( 1≤ i ≤ N ) 本目の木 i の高さは
Hi です。
あなたは、好きな順番でこれら N 本の木を全て伐採します。具体的には、
( 1, 2, … ,N ) の並び替えによって得られるある順列 P について、i = 1, 2, 3, ... , N の順に、H_{P_{i−1}}+H_{P_{i}}+H_{P_{i+1}} のコストを支払った後、木 Pi を伐採する。すなわち、H_{P_{i} } を 0 にする。
という操作を行います。ただし、H_{0}=0, H_{N+1}=0とします。
言い換えると、ある木を伐採するのにかかるコストは木を伐採する直前での、その木と両隣の木の高さの総和となります。支払うコストの総和が最小となるような P の個数を求めてください。答えは非常に大きくなる可能性があるので、(10^9+7)で割った余りを出力してください。

制約

1 ≤ N ≤ 4000
1 ≤ Hi ≤ 10^9
入力は全て整数

考察

まずは、最適な木の切り方について考えていきます。木がたくさんあると分かりにくいので、限りなく少なくします。

例１）1  5兆

高さが1の木と5兆の木があります。この2つの木を切る切り方は2通りあります。

１） 1→5兆
２）5兆→1

それぞれ計算してみましょう。

１）の場合では、まず1を切った時には、そのコストは「5兆1」となり、次に5兆を切りますので、「10兆1」が総コストになります。

２）の場合も同様に計算しますと、「5兆2」になります。

ということで2)の切り方が最適です。選ばれなかった方は2回コストがかかってしまうためにこのようになります。また、この状況ではどんなに頑張っても1+2=3回のコストがかかります。

１）1を1回、5兆を2回
２）1を2回、5兆を1回

ですので、値が小さい方を2回にした方がそうコストは小さくできそうです。

今回は木が2本でしたが3本以上ある場合には、さらに3回計上される木が出現します。この回数はその木と隣り合う2本の木と自分を含めた3本の木を切る順番によって決まります。また、この場合も全体の計上される回数はどんな順番で切っても変わりません。

でしたら、より小さい値の木に3回を割り当てて、高い木には1回を割り当てたいです。

これを踏まえて例を考えます。

例２） 4 1 8 7

先頭から行きましょう。まず4の隣には1があります(左に0があるとみなします）。ですので、1よりは先に切りたいですね。次に1です。4、8より小さいのでどんなに遅くても大丈夫です。8は1、7より大きいのでとにかくはやく切りたいです。とは言っても、4より先に切る必要はありません。あくまで隣よりも先に切りたいだけです。

このようなことを考えていくと、隣よりも先に切る、後に切るという情報だけわかれば良さそうです。

ということで、<、>の記号で表現しましょう。

4 1 8 7
 < > < 

この隣り合う不等号を満たす組であればなんでも良さそうです。例えばこんな順番が一例になります。

1 4 2 3

1 < 4
4 > 2
2 < 3

ですので、「<><」の関係が成り立ってきます。また、今回は登場しませんでしたが、同じ高さの時には「<」「>」でもどちらでもよいです。 

ここまで長々と説明してきましたが、本問題では

隣り合う数字の不等号の関係を満たす組み合わせ数

を求めることが求められています。

このような関係を求めていきましょう。このような、関係は次のようなdpを用いて求めていきます。構成は次の通りです。

dp[ i ][ j ]：
i 番目の「<」「>」の記号を考えたときに
一つ前 （ i 番目）の数字が前から j 番目にある
場合の数

です。遷移は次のようになります。

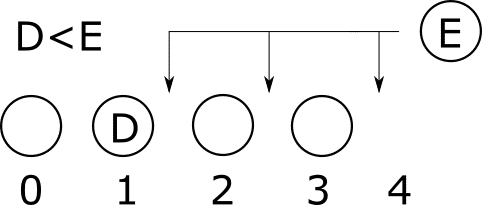
Eを考えるときに必要な情報は「Dがどこにあるか」だけです。ですので、ABCの関係は遷移に影響しません。

dp[ i+1 ][ 2 ] += dp[ i ][ 1 ]
dp[ i+1 ][ 3 ] += dp[ i ][ 1 ]
dp[ i+1 ][ 4 ] += dp[ i ][ 1 ]

と遷移します。「>」の場合には前側に挿入することができます。挿入前後で既に並んでいる個数が増えて、j がずれますのでその点注意です。特に「>」の場合には気をつけましょう。

しかし、この方法では計算時間が間に合いません。高速化が必要です。今回は累積和を使って遷移を高速化します。そのために、上図のようないわゆる「配る」dpでなく、「貰う」dpを使用します。「貰う」場合の遷移は次の通りです。

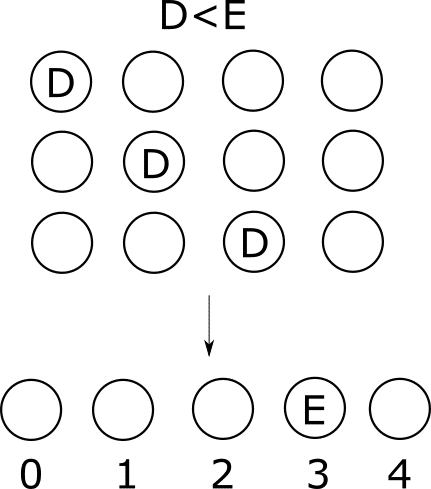
dp[ i+1 ][ 3 ] +=
 dp[ i ][ 0 ] + dp[ i ][ 1 ] + dp[ i ][ 2 ]

少し見方を変えてみました。

「現状態からどんな状態に遷移するか」

ではなく

「遷移先の状態はどんな状態から遷移されるか」

という感じです。Eの位置を一つずらしてみます。

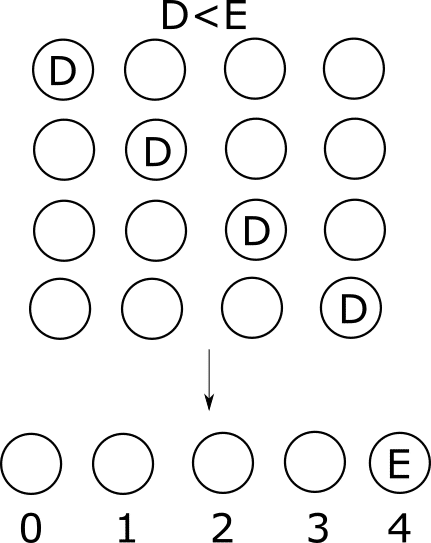
dp[ i+1 ][ 3 ] +=
 dp[ i ][ 0 ] + dp[ i ][ 1 ] + dp[ i ][ 2 ] + dp[ i ][ 3 ]

となります。なんか累積和っぽくなってきましたね。上の２つ遷移において同じ状態が出てきています。この辺まとめられそうです。

このように、累積和を管理しながら「遷移先の状態が貰う」遷移を書いていけば、無事ACがもらえます。この辺の実装方法はコメントにて補足します。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
using T = tuple<int, int, int>;

const int mod = 1e9 + 7;
class mint
{
public:
   long long x;
   mint(long long x = 0) :x((x% mod + mod) % mod) {}
   mint operator -() const { return mint(-x); }
   mint& operator +=(const mint a)
   {
       if ((x += a.x) >= mod) x -= mod;
       return *this;
   }
   mint& operator -=(const mint a)
   {
       if ((x += -a.x + mod) >= mod) x -= mod;
       return *this;
   }
   mint& operator *=(const mint a)
   {
       (x *= a.x) %= mod;
       return *this;
   }
   mint operator+(const mint a)
   {
       mint res(*this);
       return res += a;
   }
   mint operator-(const mint a)
   {
       mint res(*this);
       return res -= a;
   }
   mint operator*(const mint a)
   {
       mint res(*this);
       return res *= a;
   }
   mint pow(long long t) const
   {
       if (!t) return 1;
       mint a = pow(t >> 1);
       a *= a;
       if (t & 1) a *= *this;
       return a;
   }
   //for only prime number
   //Fermat's little theorem
   mint inv() const
   {
       return pow(mod - 2);
   }
   mint& operator/=(const mint a)
   {
       return (*this) *= a.inv();
   }
   mint operator/(const mint a)
   {
       mint res(*this);
       return res /= a;
   }
};

const int M = 4005;
mint dp[M][M];
int main()
{
   int n;
   cin >> n;
   vector<int> h(n);
   rep(i, n) cin >> h[i];
   dp[0][0] = 1;
   rep(i, n-1)
   {
       //数が等しい場合には両方処理するため「＝」となっている

       //次の数字の方が大きい場合
       if (h[i] <= h[i+1])
       {
           //j 番目までの累積和
           mint s = 0;
           rep(j,i+1)
           {
               s += dp[i][j];
               dp[i + 1][j + 1] += s;
           }
       }
       //次の数字の方が小さい場合
       if (h[i] >= h[i+1])
       {
           mint s = 0;
           //小さい場合には i 番目から減らしていく
           for (int j = i; j >= 0; --j)
           {
               s += dp[i][j];
               dp[i + 1][j] += s;
           }            
       }
   }
   //最後の数字がどこにあってもいいので
   //dpテーブルを足し合わせていく
   mint ans = 0;
   rep(i, n) ans += dp[n-1][i];
   cout << ans.x << endl;
   return 0;
}

あとがき

このように、現在の並び順に新しいものを「挿入」していくdpを挿入dpというみたいですね。私は初めて知りました。でも、不等号列「<, >」を満たす数列の数の数え上げは他の問題でも使えそうですね。これを機に覚えておきます。

また、本問題では木の切り方から、不等号列の組み合わせに言い換えるのも難しかったのはないかと思います。やはりF問題は難しいですね。