前回、ガチャコンプの確率と期待値についてnoteにまとめました。
毎週一定の閲覧数があるので、前回書かなかったことも含めて、ちゃんとまとめてみようと思います。
以下、ガチャはすべて等確率であるとします。レアとかSSRとか考えたらちょっと私の力では無理…。
高校数学レベルの内容です(ただし難関大レベル)。

この記事の中で、$${m}$$種類のガチャを$${n}$$回引いた時点で、$${k(1\leqq k \leqq m)}$$種類そろっている確率$${p(m,n,k)}$$について求めました。$${n}$$回目でちょうど揃う確率ではありません。

$$

k \geqq 2\ のとき\ p(m,n,k) = \frac{k^n\cdot _n C_k}{m^n} -\sum_{l=1}^{k-1} \frac{_m C_k \cdot _k C_l}{_m C_l}\cdot p(m,n,l) \\
k =1\ のとき\ p(m,n,1) = \frac{1}{m^{n-1}}

$$

導出は上記の記事をご覧ください。
8種類の場合について、$${n}$$回目に初めてコンプできる確率は$${p(8,n,8)-p(8,n-1,8)}$$になります。グラフにしたものが下図です。

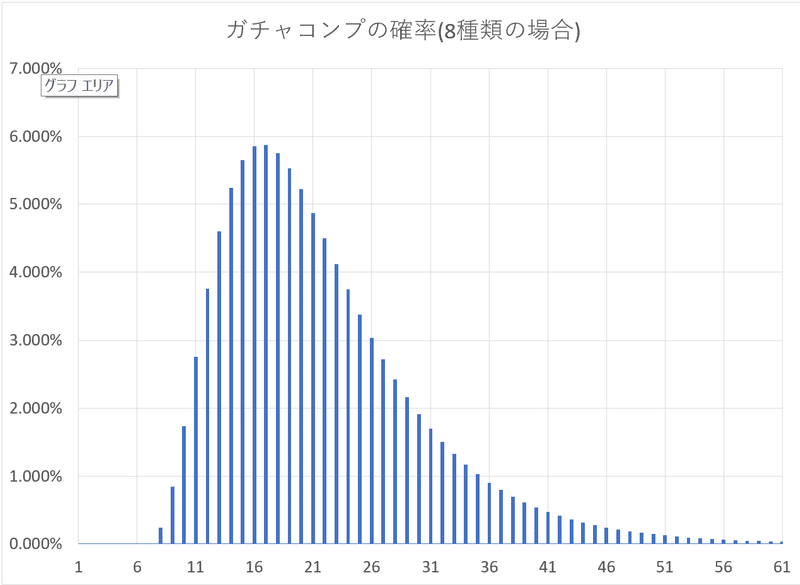
しかし、上式は再帰的で、$${p(m,n,k)}$$を求める為に、$${p(m,n,k-1),\ p(m,n,k-2),\ \cdots }$$を求めなければなりません。

この記事では、より演算速度の速い、別の方法について紹介します。

そこで、別のアプローチを試みました。
$${m}$$種類のガチャで、欲しい$${k}$$種類があるとき、$${n}$$回目までにそろう確率を、$${P_n^k}$$と定義します。

導出(証明は出来てない)は後回しにして、さきに結論から述べます。

$$
P_n^k = 1-_k C_1 \left(\frac{m-1}{m}\right)^n+_k C_2\left(\frac{m-2}{m}\right)^n-\cdots +(-1)^k\cdot _k C_k\left(\frac{m-k}{m}\right)^n \\
=\sum_{l=0}^k (-1)^l\cdot _k C_l\left(\frac{m-l}{m}\right)^n
$$

以下、簡単のため8種類の場合について考えます(すなわち$${m=8}$$)。
8種類が簡単か？というのはおいといて。
8種類のガチャにA, B, C, D, E, F, G, Hと名前をつけます。

まず、8種類のうち欲しい2種類を引く確率$${P_n^2}$$を求めましょう。
A, Bが自分の欲しいもの(当たり)、残りC~Hをはずれとします。

例として、4回以内で当たる確率を考える。
余事象の確率として、「4回まわしてもA, Bが揃わない」確率を考える。
(i)AもBも出ない場合、(ii)Aのみ出る場合、(iii)Bのみ出る場合、という場合分けを行う。

(i)の確率を求める。
すべての場合の数は$${8^4}$$通り。
AもBも出ない、すなわちC~Hのみ出る場合の数は$${6^4}$$通り。
よって確率は、$${\frac{6^4}{8^4}}$$

(ii)の確率。
Aは何回出ても良いが、0回の場合を除く。
[A, C~H]の並べ方は$${7^4}$$通り。
うち、Aが1回も出ない確率は$${6^4}$$通り。
よって確率は、$${\frac{7^4-6^4}{8^4}}$$

(iii)の確率は、(ii)と同様に$${\frac{7^4-6^4}{8^4}}$$

よって、余事象の確率は、

$$
\frac{6^4}{8^4}+\frac{7^4-6^4}{8^4}+\frac{7^4-6^4}{8^4}
=2\cdot\left(\frac{7}{8}\right)^4-\left(\frac{6}{8}\right)^4
$$

故に、求めたい確率$${P_4^2}$$は、

$$
P_4^2=1-\{ 2\cdot\left(\frac{7}{8}\right)^4-\left(\frac{6}{8}\right)^4 \}
=1-2\cdot\left(\frac{7}{8}\right)^4+\left(\frac{6}{8}\right)^4
$$

同様に考えると、n回目までに欲しい2種類がそろう確率は、

$$
P_n^2=1-2\cdot\left(\frac{7}{8}\right)^n+\left(\frac{6}{8}\right)^n
$$

各項の係数は1, -2, 1となっている。これは二項係数$${_nC_r}$$と関係ありそうだ……！

次に、3種類揃えたい場合を考えます。
A, B, Cが当たり、D~Hがはずれとして、n回目までにA, B, Cが揃う確率$${P_n^3}$$を求めましょう。

再び余事象の確率を考える。

(i) A, B, C 3種類いずれも出ない確率は、$${\left(\frac{5}{8}\right)^n}$$

(ii) A, B, C いずれか1個だけ出る場合。
A~Cから1つ選ぶ選び方は$${_3 C_1}$$通り。
仮にAを選ぶ。Aが何回出ても良い、言い換えると[A,D~H]の6種類が出るが、0回の場合、すなわち[D~H]の5種類が出る場合を除く。
上述の2種そろえたい場合の考え方を使うと、求める確率は

$$
_3C_1\cdot\frac{6^n-5^n}{8^n}=3\cdot\left(\frac{6}{8}\right)^n-3\cdot\left(\frac{5}{8}\right)^n
$$

(iii) A, B, C いずれか2個だけ出る場合。
A~Cから2つ選ぶ選び方は$${_3 C_2}$$通り。
仮にAとBを選ぶ。A, Bが何回出ても良い(C以外の7種類が出る)が、AもしくはB(選び方2通り)が0回の場合(6種類が出る)を除く。また、A, Bともに0回の場合(5種類が出る)も除く。重複に注意して数える。

$$
_3C_2\cdot\frac{7^n-2\{ 6^n-5^n\} -5^n}{8^n}=3\cdot\left(\frac{7}{8}\right)^n-6\cdot\left(\frac{6}{8}\right)^n+3\cdot\left(\frac{5}{8}\right)^n
$$

よって、余事象の確率は、

$$
\left(\frac{5}{8}\right)^n+3\cdot\left(\frac{6}{8}\right)^n-3\cdot\left(\frac{5}{8}\right)^n+3\cdot\left(\frac{7}{8}\right)^n-6\cdot\left(\frac{6}{8}\right)^n+3\cdot\left(\frac{5}{8}\right)^n \\
=3\cdot\left(\frac{7}{8}\right)^n-3\cdot\left(\frac{6}{8}\right)^n+\left(\frac{5}{8}\right)^n
$$

故に、求めたい確率は、

$$
P_n^3 = 1-\{3\cdot\left(\frac{7}{8}\right)^n-3\cdot\left(\frac{6}{8}\right)^n+\left(\frac{5}{8}\right)^n \} \\
=1-3\cdot\left(\frac{7}{8}\right)^n+3\cdot\left(\frac{6}{8}\right)^n-\left(\frac{5}{8}\right)^n
$$

この式を見ると、各項の係数が、1, -3, 3, -1となっていることが分かる。
これが$${(-1)^k\cdot _3 C_k}$$のように二項係数になっていることに注目して、一般の場合を推測したのが、結論としてあげた式である。再掲すると

$$
P_n^k = 1-_k C_1 \left(\frac{m-1}{m}\right)^n+_k C_2\left(\frac{m-2}{m}\right)^n-\cdots +(-1)^k\cdot _k C_k\left(\frac{m-k}{m}\right)^n \\
=\sum_{l=0}^k (-1)^l\cdot _k C_l\left(\frac{m-l}{m}\right)^n
$$

この式はこの記事では証明しないでおきます。たぶん数学的帰納法と二項係数の性質とか使ったら出来るんでしょうが、面倒なのでやめておきます。
それに、以下に示すとおり、コンプする場合の確率を数値計算した場合は正しい値を返しています。

n回目までにm種(全種)コンプ出来る確率は、

$$
P_n^m=\sum_{l=0}^m (-1)^l\cdot _m C_l\left(\frac{m-l}{m}\right)^n
$$

この式を使って、8種類のガチャについて、n回目までにコンプできる確率を数値計算しました。前回求めた$${p(8,n,8)}$$と比較して差を求めました。

n	p(8,n,8)	 	P_n^8		　　差
1	0.0000000000 	0.0000000000 	0.0000000000 
2	0.0000000000 	0.0000000000 	0.0000000000 
3	0.0000000000 	0.0000000000 	0.0000000000 
4	0.0000000000 	0.0000000000 	0.0000000000 
5	0.0000000000 	0.0000000000 	0.0000000000 
6	0.0000000000 	0.0000000000 	0.0000000000 
7	0.0000000000 	0.0000000000 	0.0000000000 
8	0.0024032593 	0.0024032593 	0.0000000000 
9	0.0108146667 	0.0108146667 	0.0000000000 
10	0.0281631947 	0.0281631947 	0.0000000000 
11	0.0557631254 	0.0557631254 	0.0000000000 
12	0.0933064241 	0.0933064241 	0.0000000000 
13	0.1393206837 	0.1393206837 	0.0000000000 
14	0.1917180140 	0.1917180140 	0.0000000000 
15	0.2482475596 	0.2482475596 	0.0000000000 
16	0.3067978817 	0.3067978817 	0.0000000000 
17	0.3655622114 	0.3655622114 	0.0000000000 
18	0.4231023388 	0.4231023388 	0.0000000000 
19	0.4783476425 	0.4783476425 	0.0000000000 
20	0.5305582405 	0.5305582405 	0.0000000000 
21	0.5792723223 	0.5792723223 	0.0000000000 
22	0.6242501484 	0.6242501484 	0.0000000000 
23	0.6654216742 	0.6654216742 	0.0000000000 
24	0.7028410753 	0.7028410753 	0.0000000000 
25	0.7366492133 	0.7366492133 	0.0000000000 
26	0.7670438184 	0.7670438184 	0.0000000000 
27	0.7942565489 	0.7942565489 	0.0000000000 
28	0.8185358557 	0.8185358557 	0.0000000000 
29	0.8401345615 	0.8401345615 	0.0000000000 
30	0.8593011613 	0.8593011613 	0.0000000000 
31	0.8762739868 	0.8762739868 	0.0000000000 
32	0.8912775310 	0.8912775310 	0.0000000000 
33	0.9045203642 	0.9045203642 	0.0000000000 
34	0.9161941994 	0.9161941994 	0.0000000000 
35	0.9264737644 	0.9264737644 	0.0000000000 
36	0.9355172232 	0.9355172232 	0.0000000000 
37	0.9434669545 	0.9434669545 	0.0000000000 
38	0.9504505450 	0.9504505450 	0.0000000000 
39	0.9565818977 	0.9565818977 	0.0000000000 
40	0.9619623830 	0.9619623830 	0.0000000000 
41	0.9666819828 	0.9666819828 	0.0000000000 
42	0.9708203963 	0.9708203963 	0.0000000000 
43	0.9744480853 	0.9744480853 	0.0000000000 
44	0.9776272488 	0.9776272488 	0.0000000000 
45	0.9804127204 	0.9804127204 	0.0000000000 
46	0.9828527869 	0.9828527869 	0.0000000000 
47	0.9849899297 	0.9849899297 	0.0000000000 
48	0.9868614937 	0.9868614937 	0.0000000000 
49	0.9885002854 	0.9885002854 	0.0000000000 
50	0.9899351083 	0.9899351083 	0.0000000000 

完全に一致しているのが分かります。

【感想】
texを使って数式を書くのは久々であまり慣れてないので、何とか書き上げることが出来て良かった。
【おまけ】
noteで書くときのtexの使い方をメモしておく。
$${P_n^k}$$の式を書くとき:

ただの数学の記事でした。
最後までお読みいただきありがとうございました。