前回までは、Walras均衡が成り立っている時に満たされる様々な性質について論じてきたが、そもそもWalras均衡の存在は常に保証されるのだろうか。今回は、Walras均衡の存在定理とそのために必要な条件について議論する。これまでの連載を含めたエッセンシャル版はこちら。

超過需要関数

以下では純粋交換経済：$${Y_1=\cdots= Y_J=\{0\}}$$について論じる。また、$${\forall i \in \{1, \cdots, I\}:X_i = \mathbb R_+^N}$$とし、選好関係$${≿_i}$$は連続性、厳密な凸性、強単調性を満たすと仮定する。更に$${\bar\omega = \displaystyle\sum_{i=1}^I \omega_i \in \mathbb R_{++}^N}$$とする。これらの条件の下では、任意の価格準均衡は価格均衡を成す(強単調性により示される)。

ここで、超過需要関数を、次を満たす写像$${z:\mathbb R_{++}^N\rightarrow \mathbb R^N}$$と定義する。

但し、任意の$${i}$$に対して$${x_i}$$は第$${i}$$消費者のWalras需要関数である。任意の$${i}$$に対して$${≿_i}$$は厳密な凸性を満たすため$${x(p, p\cdot\omega_i)}$$は1点集合であり、従って超過需要対応は関数である。

価格ベクトル$${p}$$がWalras均衡価格ベクトルであることと、$${z(p)=0}$$は同値である。$${z(p)>0}$$の時は超過需要、$${z(p)< 0}$$の時は超過供給である。

任意の$${i}$$に対して$${X_i=\mathbb R_+^N}$$とし、$${\bar\omega =\displaystyle \sum_{i=1}^I \omega_i \in \mathbb R_{++}^N}$$と仮定する。選好関係$${≿_i}$$は連続性、厳密な凸性、強単調性を満たすとする。$${Y_1=\cdots= Y_J=\{0\}}$$とする。この時、超過需要関数$${z}$$は以下の性質を持つ。

• 連続性：$${z}$$は連続である

• 0次同次性：$${z}$$は0次同次である

• Walras法則：$${\forall p \in \mathbb R_{++}^N: p\cdot z(p)=0}$$

• 下への有界性：$${z}$$は下に有界、つまり$${\exist s \in \mathbb R, \forall n \in \{1, \cdots, N\}, \forall p \in \mathbb R_{++}^N: z^n(p) ≥ s}$$、但し$${z^n(p)}$$は$${z(p)}$$の第$${n}$$成分である

• 境界挙動条件：$${\mathbb R_{++}^N}$$内の点列$${(p_1, p_2, \cdots)}$$が価格ベクトル$${p \in \mathbb R_+^N \setminus (R_{++}^N \cup \{0\})}$$(0の成分が必ずあるが全てではないようなベクトル)に収束するとき、$${\max \{z^1(p_k), \cdots, z^N(p_k)\} \rightarrow \infin (k \rightarrow \infin)}$$である。但し$${z^n(p_k)}$$は$${z(p_k)}$$の第$${n}$$成分を表す

境界挙動条件は、ある財の価格がゼロに収束するとき、なんらかの財の消費が予算制約上で無限に消費できるようになり、かつ強単調な選好の場合はより多くの消費を好むため消費量が無限大に発散する、という条件である。

連続性、0次同次性、Walras法則、下への有界性は、それぞれ各消費者の需要関数が同様の性質を持つことから直ちに導出される。境界挙動条件も以下の証明により、各消費者の需要関数の性質から導ける。$${p\cdot \big(\sum_{i=1}^I \omega_i\big)>0}$$より、少なくとも一つの$${i}$$に対しては$${p\cdot \omega_i > 0}$$である。この$${i}$$ に対し、

$${\max\{x_i^1(p_k, p_k \cdot \omega_i), \cdots, x_i^N(p_k, p_k \cdot \omega_i)\}\rightarrow \infin  (k \rightarrow \infin)}$$

を示せば十分である。背理法で証明しよう。数列$${(\max\{x_i^1(p_k, p_k \cdot \omega_i), \cdots, x_i^N(p_k, p_k \cdot \omega_i)\})_{k=1}^\infin}$$を上に有界と仮定する。$${X=\mathbb R_+^N}$$なので、この数列は下にも有界であり、従って有界な部分列が存在する。その部分列を再び$${(\max\{x_i^1(p_k, p_k \cdot \omega_i), \cdots, x_i^N(p_k, p_k \cdot \omega_i)\})_{k=1}^\infin}$$と書くことにする。

点列$${(\{x_i^1(p_k, p_k \cdot \omega_i), \cdots, x_i^N(p_k, p_k \cdot \omega_i)\})_{k=1}^\infin}$$の極限を$${v \in \mathbb R_+^N}$$と書く。Walras需要関数に対するWalras法則より、$${p_k\cdot x_i(p_k, p_k \cdot \omega_i)=p_k\cdot \omega_i}$$より、$${k\rightarrow \infin}$$とすれば$${p_k\cdot v=p_k\cdot \omega_i}$$を得る。

もし$${v}$$が価格$${p}$$の下での選好最大化問題の解なら、これは選好関係$${≿_i}$$の強単調性に矛盾するため、これを示す。そこで、$${p\cdot x_i ≤ p \cdot \omega_i}$$とする。ここで$${x_{i, k}=\dfrac{p_k\cdot \omega_i}{p_k\cdot x_i}x_i}$$とすると、$${p_k\cdot x_{i,k}=p_k\cdot \omega_i}$$を得る。従って、$${x_i(p_k, p_k \cdot \omega_i)≿_i x_{i, k}}$$が成り立つ。選好関係$${≿_i}$$は連続より、$${k → ∞}$$の時、$${\dfrac{p_k\cdot \omega_i}{p_k\cdot x_i}\rightarrow \dfrac{p\cdot \omega_i}{p\cdot x_i}}$$となるため、$${v ≿_i \dfrac{p\cdot \omega_i}{p\cdot x_i}x_i}$$が成立する。$${≿_i}$$は強単調なので、$${\dfrac{p\cdot \omega_i}{p\cdot x_i}≥ 1}$$より$${\dfrac{p\cdot \omega_i}{p\cdot x_i}x_i≿_i x_i}$$、よって$${v ≿_i x_i}$$が成立する。このように$${v}$$は$${p}$$の下での選好最大化問題の解であるという矛盾が得られた。

ただし、境界条件が満たされるからと言って$${p_k^n → 0}$$ならば必ず$${z^n(p_k) → ∞}$$であるとは限らないことに注意(価格がゼロに収束する財と超過需要が無限大に発散する財が異なる場合もある)。

効用最大化問題と超過需要関数

3財1消費者の経済で以下のような例題を考える。初期保有量は$${\mathbb R_{++}^3}$$に属すると仮定する。選好関係は効用関数$${u:\mathbb R_+^3 \rightarrow \mathbb R}$$で表されるとする。超過需要関数を$${z}$$で表し、その第$${n}$$成分を$${z_n}$$とする。$${p \in \mathbb R_+^3 \setminus \{0\}}$$とし、$${p_1, p_2, \cdots}$$を、$${p}$$に収束する$${\mathbb R_{++}^3}$$内の点列とする。この時、

1. 効用関数$${u}$$が$${u(x_1, x_2, x_3)=x_1\sqrt{x_2}\sqrt{x_3}}$$で定義されるとき、$${\forall n: p_n = 0 \Rightarrow k \rightarrow \infin}$$の時$${z_n(p_k) \rightarrow \infin}$$を証明せよ

2. 効用関数$${u}$$が$${u(x_1, x_2, x_3)=x_1+\sqrt{x_2}+\sqrt{x_3}}$$で定義されるとき、上記で証明された性質は成り立つか

1.の証明
この効用関数の下でのLagrangian$${\mathcal L = x_1\sqrt{x_2}\sqrt{x_3}-\lambda p\cdot z(p)}$$と予算制約式：$${p\cdot z(p)=0}$$からLagrangeの未定乗数法により、各財の需要関数は以下のように求まる。

$${x_1(p) = \dfrac{1}{2p_1}p\cdot z(p),     x_2(p) = \dfrac{1}{4p_2}p\cdot z(p),     x_3(p) = \dfrac{1}{4p_3}p\cdot z(p)}$$

従って初期保有と価格ベクトルの内積は定数より、$${\forall n: p_n = 0 \Rightarrow k \rightarrow \infin}$$の時$${z_n(p_k) \rightarrow \infin}$$が成り立つ。

2.の証明
同様に需要関数を求めると、

$${x_1(p)=\dfrac{1}{p_1}p\cdot z(p)-1,          x_2(p)=\bigg(\dfrac{p_1}{2p_2}\bigg)^2,          x_3(p)=\bigg(\dfrac{p_1}{2p_3}\bigg)^2}$$

となる。$${x_2(p)}$$と$${x_3(p)}$$については、$${p_1=0}$$の時に上記の性質が必ず成り立つとは限らない。

Walras均衡の存在

これまでWalras均衡の性質を論じてきたが、その存在は常に保証されるのだろうか。実はWalras均衡は上述の仮定の上で存在することが知られている。

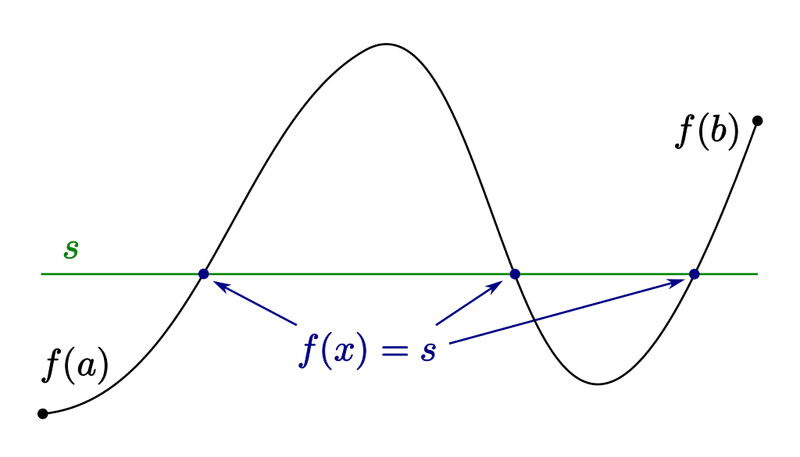
本格的な証明を与える前に、中間値の定理によって簡単に示すことができる。$${N=2}$$の場合で考察してみよう。$${N=2}$$の場合はグラフを用いて視覚的に表現でき、またより一般的な場合への示唆を与えるという点でも重要である。価格ベクトルを$${(p^1, 1)}$$とする(但し$${p^1>0}$$)。

Walras法則から第 1 財に関してのみ論じれば良いから、Walras均衡の存在を示すには$${z_1(p^1, 1)=0}$$となるような$${p^{1∗}}$$が存在することを示せばよい。境界挙動条件より、もし$${p^1}$$が十分に小さければ第 1 財には超過需要が発生するから$${z_1(p^1 , 1) > 0}$$ が成立する。一方、もし$${p^1}$$が十分に大きければ第 1 財には超過供給が発生するから$${z_1(p^1 , 1) < 0}$$ が成立する。超過需要関数$${z_1(p^1 , 1)}$$は連続だから、中間値の定理により、確かに少なくともひとつの$${p^{1∗}}$$が存在して$${z_1(p^{1∗} , 1) = 0}$$が成立することが分かる。

存在定理の仮定と不動点定理

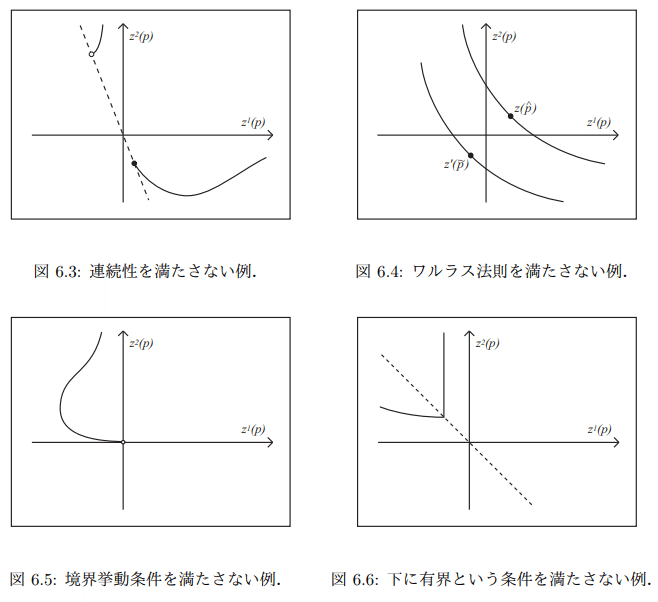
Walras均衡の存在定理は上述の性質を満たす関数$${z}$$に対し、$${z(p) = 0}$$となる価格体系$${p}$$が存在することを示せば十分である。ここでは$${N = 2}$$のケースにおいて$${z}$$が0 次同次性を除く4性質のうち1つを満たしていなければ、$${z(p) = 0}$$を満たす$${p \in \mathbb R_{++}^N}$$が存在しないことを図を用いて示す。0 次同次性が満たされない場合でも、残りの4性質を満たせば均衡は存在する。0 次同次性は均衡の存在ではなく局所的一意性を保証するために欠かせない。

以下の4つの図は、0次同次性以外のいずれか一つの条件に抵触している。

均衡の存在定理のために次の定理を用いる。この定理の証明には数学的な準備が必要なため ここでは省略する。

角谷の不動点定理はコンパクト集合からそれ 自身への対応に関して成立している命題であるため$${z}$$に直接適用することができず、少し工夫を要する。

$${\mathbb R_+^N}$$の部分集合$${P}$$を、$${P=\{p \in \mathbb R_+^N| \sum_{n=1}^N p^n =1\}}$$と定める。この時$${P}$$は非空、凸、コンパクト集合である。$${P}$$の内部を$${\text{int} P \equiv \{p \in P | \forall n : p^n > 0\}}$$、境界を$${\partial P \equiv \{p \in P | \exist n : p^n = 0\}}$$と定義する。対応$${f:P \twoheadrightarrow P}$$を、

$${f(p)=\begin{cases} \{q \in P| \forall r \in P: z(p)\cdot q ≥ z(p) \cdot r\},    \text{for}   p \in \text{int} P \\ \{q \in P| p\cdot q =0\},    \text{for}   p \in \partial P \end{cases}}$$

によって定める。$${f}$$の定義と以下は同値である。

$${f(p)=\begin{cases} \{q \in P| z^n < \max_m z^m(p) \Rightarrow q^n =0\},    \text{for}   p \in \text{int} P \\ \{q \in P| p^n > 0 \Rightarrow q^n =0\},    \text{for}   p \in \partial P \end{cases}}$$

対応$${f}$$は市場の価格調整メカニズムを表現していると解釈できる。つまり調整前価格ベクトル$${p}$$と調整後価格ベクトル$${q \in f(p)}$$を比較すると、超過需要$${z^n(p)}$$が相対的に小さな財$${n}$$について$${q^n < p^n}$$が成り立っている。

$${f}$$の定義より$${p}$$が$${f}$$の不動点ならば$${p \in \text{int} P}$$であり、また簡単な議論から$${f}$$の任意の不動点がWalras均衡価格であることが分かる。ゆえに$${f}$$が角谷の不動点定理の仮定を満たすことを示せば証明が完了する。また任意の$${p}$$に対し、$${f(p)}$$が凸、非空であることは定義から明らかであるので、閉グラフを持つことを示せば十分である。

Euclid空間で集合$${A}$$が閉であるとは、 集合内の任意の収束列の極限が$${A}$$に属することと同値である。$${P × P}$$上の点$${(p, q)}$$に収束す るグラフ上の収束列$${\{(p_k, q_k)\}}$$ を任意にとる。つまり$${q_k \in f(p_k)}$$とする。ここで$${p \in \text{int} P}$$の場合と$${p \in \partial P}$$の場合に分けて$${q \in f(p)}$$を示す。他のケースもあり得るのだが、これらの2つの場合を考えれば十分である。

$${(\text{i})    p \in \text{int} P}$$の場合
$${p}$$が内点であるので、十分大きな$${k}$$に対して$${p_k \in \text{int} P}$$が成立する。この場合、任意の$${r \in P}$$に対して$${z(p_k) \cdot q_k ≥ z(p_k) \cdot r}$$が成立する。極限をとると、$${z(p)\cdot q ≥ z(p) \cdot r}$$であり、従って$${q \in f(p)}$$である。

$${(\text{ii})    p \in \partial P}$$の場合
$${p^n >0 \Rightarrow q^n =0}$$であることを示す。もし$${p_k \in \partial P}$$ならば、十分大きな$${k}$$に対して$${p_k^n >0}$$なので定義から$${q_k^n = 0}$$。そこで一般性を失うことなく$${p_k \in \text{int} P}$$とする。まず境界挙動条件より、点列$${p_k}$$がベクトル$${p\in \mathbb R_+^N \setminus (\mathbb R_{++}^N \cup \{0\})}$$に収束するとき、$${\max_m z^m(p_k) \rightarrow \infin}$$が成立する。

次に、任意の$${n}$$について$${p^n >0}$$ならば$${(z^n(p_k))_k}$$は上に有界であることを示す。$${s}$$を、任意の$${p \in \mathbb R_{++}^N}$$と任意の$${n}$$に対して$${z^n (p_k) > s}$$が成立する定数とすると、

$${z^n(p_k) =-\dfrac{1}{p_k^n}\displaystyle \sum_{m \not= n}p_k^mz^m(p_k) < -\dfrac{1}{p_k^n}\displaystyle \sum_{m \not= n}p_k^ms < -\dfrac{s}{p_k^n} < -\dfrac{2s}{p^n}}$$

となる。ここで最右辺の不等式は、十分大きな$${k}$$に対し$${p_k^n >p^n/2}$$と取れることによる。以上より、任意の$${n}$$に対して$${p^n >0}$$ならば$${(z^n(p_k))_k}$$も有界である。従って十分大きな$${k}$$に対しては$${z^n(p_k) < \max_m z^m(p_k)}$$が成立する。よって$${q_k^n=0}$$であり、$${q^n=0}$$である。