奇妙なタイトルと思うかもしれない．人生の一部をインターネット上で過ごす時代である．
サイトが出現し，それがコンテンツで埋め尽くされ，それらが結びつけ（リンク）られる． すべて自然発生的なもので，誰かが明示的に制御しているわけではない．
多数の「自由」な要素からなる他の複雑系と同様に，インターネットは，
全体として，細部の乱れに依存しない安定した性質を持ち，数学的に調べることができる媒体となる．
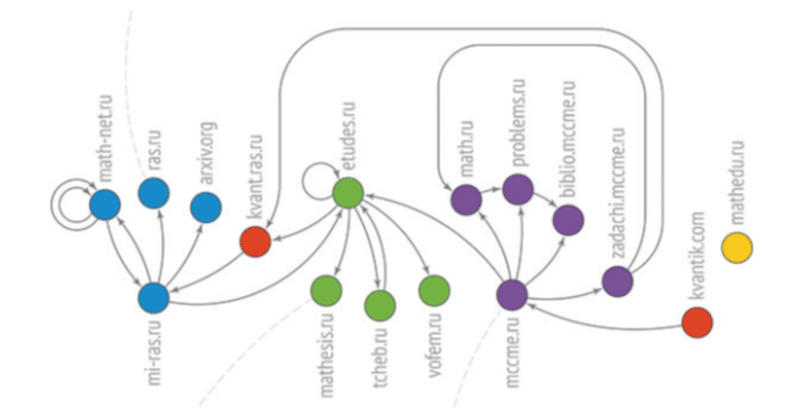
ここでは，インターネットをグラフで表現することにする．
グラフとは，有限個の円弧（グラフ辺）で結ばれた点（グラフ頂点）の集合で，頂点はインターネットのサイト，辺はあるサイトから別のサイトへのハイパーリンクである．
このグラフのエッジには方向性がある（誰が誰にリンクするかが重要）．リンクには多重リンク（あるサイトから別のサイトへの複数のリンク）もあり，ループ（同じサイトのページ間のリンク）もある．
ウェブのグラフは，何十億もの頂点と辺を持つ怪物である．
このグラフは常に変化しており，サイトが追加されたり消滅したり，リンクが消えたり現れたりしている．
しかし，そのような変化にもかかわらず，インターネットのいくつかの特性は，研究の歴史を通じて変わることがなかった．

ここでは，そのような「安定した」特性の例をいくつか紹介する．
ウェブのグラフはまばらであり，辺の数は頂点の数の数倍（頂点の数より数倍多いだけ）程度である．あらゆる種類のリンクが可能なのに，それでもまだ辺の数は十分ではないのは不思議なことである．
まばらではあるが，インターネットの世界はとても狭い．
すなわち，5〜6回の「クリック」で，どのウェブサイトからもリンクを介して他のウェブサイトに移動することが可能である（有名な「6つの握手の法則」）．
ウェブのグラフでは， ある頂点の「隣人」（この頂点にリンクしているサイト）は，高い確率でそれ自体が辺で結ばれている："私の知り合いは知り合い "である．
グラフの頂点の重要な特性は，頂点の次数（注入する辺と流出する辺の数）とその数が，ある法則に従って分布していることである：
次数$${d}$$の頂点の割合は，$${1/d^γ}$$に比例する．ここで$${γ≒2.3}$$である．
この式には明確な「カーネル」があり，高次数$${d}$$のノード（リンク数の多い（頂点）サイト）のシェアは小さい．
しかし，驚くべき詳細がある．定数$${γ}$$はウェブグラフの頂点数に依存しない，つまり，インターネットの進化に伴って変化しないのだ．この冪乗則は，$${γ}$$がネットワークごとに微妙に異なることを除けば，生物学的ネットワークから銀行間ネットワークに至るまで，複雑なネットワークに普遍的なものである．
インターネットは全体として，サイトへのランダムな攻撃に対して回復力がある．すなわち，サイトの破壊が独立かつ等確率で起こる場合，確率が1に近いウェブのグラフは「巨大な」接続性成分を保持する．
この成分は、攻撃されたハブの割合がある臨界値を超えない限り、ハブ（最も次数の高い頂点）をターゲットにしても維持される．

インターネットを知るには，「偶然のグラフ」モデルを構築できるようになる必要がある．それは，実際のインターネットが持つ期待される特性を高い確率で持っているものだ．
しかし，実用上はもちろん，純粋に数学的な目的でも，モデルが複雑すぎないことが肝要である．この困難で魅力的な課題は，完全には解決されていない．
インターネットの優れた数学的モデルを構築することは，情報検索の改善，スパムの特定，拡散の予測など，インターネット全体やソーシャルネットワークにおける質的に新しいツールに直結します．

一方，インターネットの数学的モデルは，生物群集のモデルや銀行間相互作用のモデルに非常に似ている．生物学的あるいは金融的なコミュニティの研究は，インターネットよりもずっと早く始まったが，後者の発展の激しさとその研究の進歩は，これらすべてのモデルの相互影響を豊かなものにしている．

このようなシステムの研究は，応用数学の中心的な分野であり，すべての数学にとっても新しい問題の無尽蔵の源泉である．

Райгородский
Андрей Михайлович　p.16-17
応用：コンピュータネットワーク、生物学、金融
数学：離散数学、グラフ理論