フォースプレートの力学

はじめに

前章で，フォースプレートで計測可能な４つの物理量について概説したが，ここで，その物理的意味と数理について述べる．

なお，本章ではバイオメカニクスの解析を意識し，「身体に作用する力（＝床・地面に作用する反力）」として床反力（地面反力，ground reaction force）を記述し，座標系も解析用の$${z}$$軸が鉛直上向きの座標系を使用する．一方，多くのフォースプレートメーカーは，$${z}$$軸が鉛直下向きの座標系を採用し，「床に作用する力（＝身体に作用する反力）」という，あえて床反力という名称とは反対の力を出力している．

また，本章の多くの式は成分表示せず幾何ベクトルのまま記述しているが，成分を記述した一部の式では座標系の選択の仕方に依存して式の成分が異なるので注意されたい．このことについては最後の補足10に記載した．

１．床反力（ground reaction force）

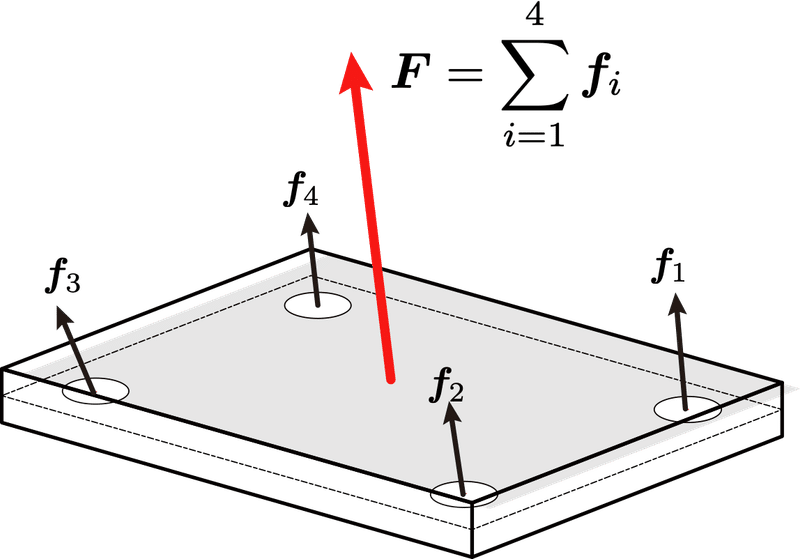
通常，フォースプレートは４つの３軸力覚センサを備え，各方向の合力を床反力（地面反力）ベクトル$${\bm{F}}$$として出力する．ここでイタリック・ボールドの記号はベクトルを意味し，各力覚センサの出力を$${\bm{f}_1,\bm{f}_2,\bm{f}_3,\bm{f}_4}$$とすると，床反力$${\bm{F}}$$は

$$
\bm{F} = \sum_{j=1}^4 \bm{f}_j = \bm{f}_1 +\bm{f}_2 +\bm{f}_3 +\bm{f}_4
$$

となる．

なお，ここでは床反力を，地面反力，すなわち身体が地面から受ける反力として定義し，上向きに図示している．

２．力のモーメント（moment of force）

モーメントは能率，積率などと呼ばれ，原点（中心）からの距離に応じて変化し，力学では回転と密接に関係した物理量である．力学におけるこの他のモーメントとしては，慣性モーメント，角運動量などがあり，慣性モーメントは質量分布に関係する回しにくさ，角運動量は回転の運動量（回転の勢い）と関係した物理量である．

モーメントについては補足１を参照されたい．

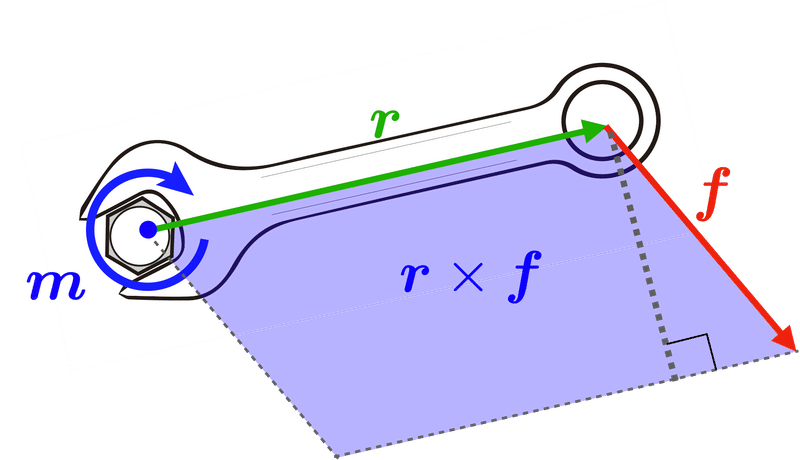
力のモーメント$${\bm{m}}$$は，力ベクトルに関する１次のモーメントで，座標系の原点（中心）からの距離に比例し，その物体を回転させるための力（回転力）を意味する．図２のような原点（中心）からみた位置ベクトル$${\bm{r}}$$の位置に力$${\bm{f}}$$が作用しているとすると，そのとき回転力，すなわち力のモーメントは，

$$
\bm{m} = \bm{r} \times \bm{f}
$$

で与えられる．ここで記号（$${\times}$$）は外積を表す．外積については

を参照されたい．

図２のようにレンチでネジを回す際，ネジを回す力の大きさ，すなわち力のモーメントは，ネジの中心から力の作用点までの位置ベクトル$${\bm{r}}$$と力ベクトル$${\bm{f}}$$が作る外積（$${\bm{r} \times \bm{f}}$$）の大きさ（図２の青の領域の面積）で決まる．この外積の意味から，力$${\bm{f}}$$が$${\bm{r}}$$の位置ベクトルと垂直になる時にもっとも大きな力のモーメントを与える．反対に，$${\bm{f}}$$と$${\bm{r}}$$が平行になる時に力のモーメントは$${0}$$となる．これは図２のレンチが作る力のモーメントの大きさを表す面積で考えるとわかるであろう．

さて，力のモーメント$${\bm{m}}$$は，原点が異なるとその値も異なる物理量で，このような座標系の原点の選択に依存するベクトルを束縛ベクトル（bound vector）と呼ぶ（補足６参照）．フォースプレートの場合，原点は通常フォースプレートの上板の下面，または力覚センサの原点の高さに設定し，各力覚センサから等距離のフォースプレートの中心$${\text{S}}$$に定められる．また，フォースプレートでモーメントといえば，ほぼ力のモーメントを指すので，省略して単にモーメントと呼ばれることが多い．

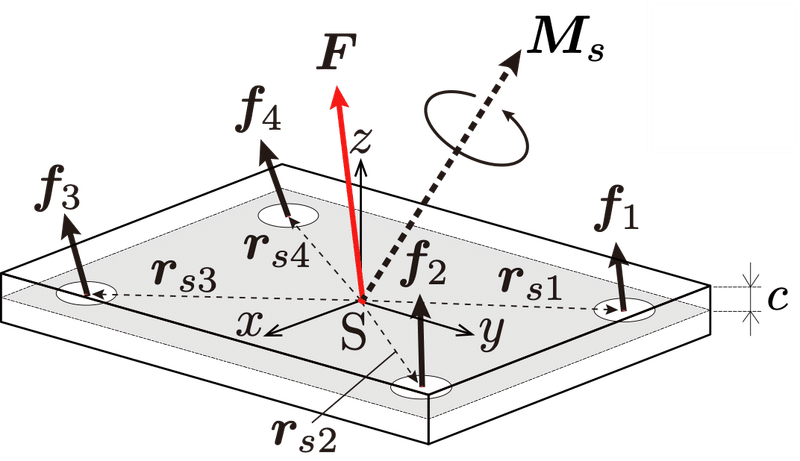
一般的なフォースプレートには４箇所に力覚センサが装備されているので，フォースプレート座標系の原点を$${\text{S}}$$とすると，原点$${\text{S}}$$まわりの力のモーメント$${\bm{M}_s}$$は

$$
\bm{M}_s = \sum_{j=1}^4 \left(\bm{r}_{sj} \times \bm{f}_j \right)
$$

で与えられる．ここで，$${\bm{r}_{sj}}$$は原点$${\text{S}}$$から各センサ$${j (j=1,\cdots ,4)}$$への位置ベクトルを表し，$${\bm{f}_j}$$は各センサ$${j}$$に作用する（で計測される）力ベクトルを表す．

くどいが，モーメントは座標系の原点の選択に依存した束縛ベクトルであって，通常メーカが定めた座標系（センサ座標系）の原点まわりの力のモーメントが出力されることに留意されたい．そして，次のCOPの計算ではこの原点の位置（フォースプレート表面からセンサ座標系の原点までの距離）が計算に必要となる．

なお，物体に力$${\bm{f}}$$が作用し，その力に関する原点$${\text{O}}$$回りの力のモーメント$${\bm{m}_O}$$が既知で，さらに異なる原点$${\text{O}'}$$まわりの力のモーメント$${\bm{m}_{O'}}$$を知りたい時に，$${\text{O}}$$から見た$${\text{O'}}$$の位置ベクトルが$${\bar{\bm{r}}}$$であることも利用すれば，平行軸の定理を用いて

$$
\bm{m}_{O'} = \bm{m}_{O} + \bar{\bm{r}} \times \bm{f}
$$

のようにモーメントの座標変換を行い簡単に$${\bm{m}_{O'}}$$を計算することができる．平行軸の定理については補足５を参照されたい．

３．圧力中心（COP，center of pressure）

フォースプレートには力が分布して作用する．このとき総和の力（床反力）が作用する代表点をCOP（圧力中心，足圧中心）と呼ぶ．圧力中心は力分布の重心点で，フォースプレートに作用する各力がつくる，全ての力のモーメントが釣り合う点である．

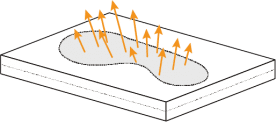
ここでは，さらにCOPの物理的意味について以下で説明を行う．図４のように足でフォースプレートを踏んでいる際，力は接触している部分に分布して３次元方向の各方向に作用する．ここで，この力の鉛直方向成分だけを示したのが図５になる．

図５では，この力分布を，鉛直力の矢印の先が作る曲面とフォースプレートの表面で構成される均一な密度の塊として表現した．このグレーの物体だけ取り出し，「グレーの塊に対して，その下側の床面でバランスのとれる点」がCOPに相当する．このCOPに，合力である１つの床反力$${\bm{F}}$$が作用していると考えてよく，この「代表点」をCOPと呼び，これは床反力の重心を意味する．

なお，床反力には水平力が含まれるが，力の釣り合いを考えたときに，水平方向に作用する力はバランス，すなわち力のモーメントの計算には影響しない．したがってCOPの計算には鉛直力だけが寄与する．

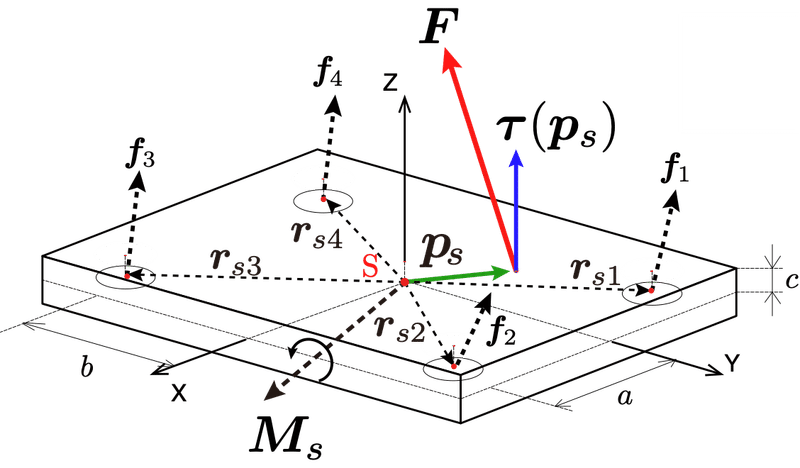
さて，具体的にフォースプレートの出力を利用したCOPの計算方法であるが，１で述べた床反力を$${\bm{F}=[F_x~F_y~F_z]^T}$$，２で述べた原点$${\text{S}}$$まわりの力のモーメントを$${\bm{M}_s = [M_{sx}~M_{sy}~M_{sz}]^T}$$とするとき（図６参照），フォースプレートのCOPの位置ベクトル$${\bm{p}_s=[p_x~p_y~c]^T}$$の$${x,y}$$成分$${p_x, p_y}$$は

$$
p_x = \frac{-M_{sy}+c F_{x}}{F_{z}}\\ p_y =\frac{M_{sx}+c F_{y}}{F_{z}}
$$

で与えられる．ここで，$${c}$$は原点$${\text{S}}$$とフォースプレート表面までの鉛直方向の距離パラメータである（図６参照）．

このCOP（$${p_x, p_y}$$）の導出は補足２，３を参照されたい．

なお，COPの算出では$${F_z}$$による除算を含んでいる．したがって，特に小さい$${F_z}$$に対して，COPの誤差が生じやすい．

この事も踏まえ，COPの計算に関して，さらに以下のことにも留意されたい．

• フォースプレートのアンプは，計測前の無負荷状態で常にゼロリセットなどを行い，オフセットを取り除く．

• 無負荷状態でもフォースプレートの出力にノイズを含むので，COPの計算に$${F_z}$$に対する閾値を設けて，閾値以下の場合，COPの計算を行わない．

• フォースプレートの計測，特にCOPの計算では，フォースプレートに対して表面から下方に押す力を想定している．吸盤で固定したり身体とフォースプレート間の粘着物質を使用するなどして，上方に引っ張るような力を与えたり，フォースプレートの側面に力を与えてはいけない．

• フォースプレートの上に何らかのマットやシートを敷いている場合，その厚さをパラメータ$${c}$$に加えてCOPの計算を行う必要がある．

４．摩擦モーメント（frictional moment, vertical moment）

COPは，水平方向を軸とする力のモーメントがバランスする点として定義した．しかし，鉛直軸回りの力のモーメントは残り，これが摩擦モーメントである．この摩擦モーメントは，フォースプレートと身体（足）間の摩擦力全体がつくる，ひねり・ねじりに相当する力のモーメントベクトルで，フォースプレートの面に対して垂直な鉛直軸回りのベクトルである．

一般的にはこれはフリーモーメント（free momen）と呼ばれるが，ここでは摩擦モーメントと呼ぶこととする．

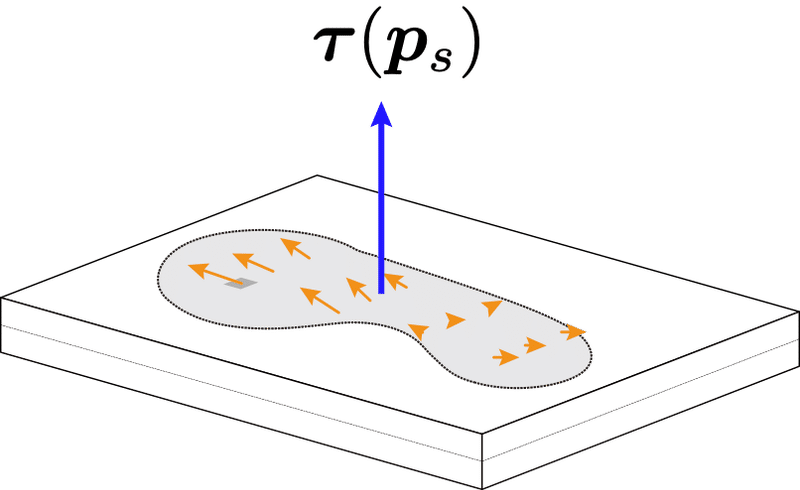
フォースプレートの摩擦モーメント$${\bm{\tau}(\bm{p_s})}$$は

$$
\bm{\tau}(\bm{p}_s) = \begin{bmatrix} 0 \\ 0 \\ \tau_{z} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ M_{sz} + p_{y} F_{x} -p_{x} F_{y} \end{bmatrix}
$$

で与えられる（図６参照）．ここで，摩擦モーメントを$${\bm{\tau}(\bm{p_s})}$$をあえてCOPの位置ベクトル$${\bm{p}_s}$$の関数で示した理由は，これが原点$${\text{S}}$$とCOPの位置に依存して決まることを示しているためである．

摩擦モーメントの導出は補足２，３を，これに関連して偶力，自由ベクトルなどについては補足６，７，８を参照されたい．

ここまで，フォースプレートに関係する基本的な力学を述べた．次章「複数のフォースプレートによる計測」では，複数のフォースプレートを使用する際に必要となる，合成のCOPについて述べる．なお合成のCOPの計算でも平行軸の定理が必要となる．

補足

補足１：モーメント

モーメントは，力学にとどまらず多くの分野で用いられる用語である．

回転半径，すなわち原点からの距離の０乗に比例するモーメントを０次モーメント，距離の１乗に比例するモーメントを１次モーメント，２乗に比例するモーメントを２次モーメント，$${n}$$乗に比例するモーメントを$${n}$$次モーメントと呼ぶ．

ここでは，質量分布に関する以下の３つのモーメントを例として取り上げる．密度$${\rho}$$の物体を考え，その０次のモーメントは

$$
\begin{aligned}
m&=\int_V \rho~ dV\\&= \iiint_{xyz} \rho~ dxyz
\end{aligned}
$$

と書ける．これは密度$${\rho}$$の微小な体積$${dV}$$を全て足し合わせるという意味であり，２行目は３方向に渡って積分することと等しいことを示している．

0次のモーメントは，原点からの長さ$${\bm{x}}$$の０乗，すなわち距離と無関係であるので，密度$${\rho}$$を微小体積$${dV}$$を全て加算するだけとなり，質量$${m}$$となる．

密度$${\rho}$$の１次のモーメントを質量$${m}$$で割ると

$$
\bm{x}_G=\frac{1}{m}\int \bm{x}\rho ~dV
$$

重心$${\bm{x}_G}$$となる．微小体積$${dV}$$に原点からの長さ$${\bm{x}}$$を掛けたものの積分なので，原点から遠いほど重みがかかって加算されることを示している．

密度$${\rho}$$の２次のモーメント

$$
\bm{J}=\int \bm{x}^2\rho ~dV
$$

は距離の２乗に比例する慣性モーメント$${\bm{J}}$$となる．

ここでは物理量として「スカラ」である密度の分布に関するモーメントを取り上げた．この他に，力のモーメントや角運動量のような，「ベクトル」に関するモーメントがあり，ベクトルのモーメントの場合，回転中心（原点）からの位置ベクトル$${\bm{r}}$$との外積で計算を行うことになる．

力のモーメントは$${\bm{r} \times \bm{f}}$$のように$${\bm{r}}$$と力$${\bm{f}}$$との外積で記述され，角運動量は$${\bm{r} \times m\bm{v}}$$のように$${\bm{r}}$$と運動量$${m\bm{v}}$$との外積で記述される．

補足２：圧力中心と摩擦モーメントの力学と物理的意味

ここでは，「３．COP」と，「４．摩擦モーメント」の物理的意味をモデルを使用して示す．

COPは，定義から床反力の重心点であることを３で述べた．すなわち，COPの位置では鉛直方向の力分布がつくる水平軸まわりの力のモーメントが０であることが求められるが，水平方向の摩擦力がつくる鉛直軸回りの力のモーメントは残る．ここでは，このことをモデルで確認する．

図８に示すように，床反力の分布を，鉛直方向の力分布$${\sigma_z (x, y)}$$と水平方向の力分布$${\sigma_x (x, y), \sigma_y (x, y)}$$に別けて考える（文献１）．

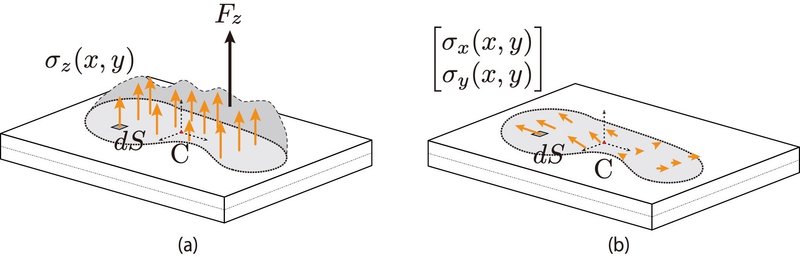
ここで，「フォースプレート表面上に原点をもつ座標系$${\text{C}}$$」を考え，フォースプレート表面の位置ベクトル$${\bm{r}=[x~y~0]^T}$$にある微小な単位面積$${dS}$$を考え，この単位面積に鉛直方向の床反力$${\sigma_z (x, y)}$$が分布して作用する（図８(a)参照）．また，同様に$${dS}$$に作用する水平方向の床反力を$${\sigma_x (x, y), \sigma_y (x, y)}$$（図８(b)参照）とし，これらをまとめて

$$
\bm{\sigma}(x,y)=\begin{bmatrix}\sigma_x(x,y) \\ \sigma_x(x,y) \\ \sigma_x(x,y)\end{bmatrix}
$$

と与える．この$${\bm{\sigma}(x,y)}$$を積分し，全てを加算すれば

$$
\bm{F}=
\begin{bmatrix}
F_{x}\\ F_{y}\\ F_{z}
\end{bmatrix}
=
\int_{S}
\begin{bmatrix}
\sigma_{x}(x,y)\\ \sigma_{y}(x,y) \\ \sigma_{z}(x,y)
\end{bmatrix}
dS
\equiv
\int_{S} \bm{\sigma}(x,y)~ dS
$$

のように床反力ベクトル$${\bm{F}}$$となる．これは力ベクトル$${\bm{\sigma}}$$の０次のモーメントに相当する．

そこで，フォースプレートの表面の位置ベクトル$${\bm{p}_c=[p_x~p_y~0]^T}$$まわりの力のモーメント$${\bm{m}(\bm{p}_c)}$$を考えると，

$$
\bm{m}(\bm{p}_c) = \int_S (\bm{r}(x,y)- \bm{p}) \times \bm{\sigma}(x,y) ~dS \\
= \int_{S} \left( \begin{bmatrix} x - p_{x} \\ y -p_{y}\\ 0 \end{bmatrix} \times
\begin{bmatrix}
\sigma_{x}(x,y)\\ \sigma_{y}(x,y)\\ \sigma_{z}(x,y)
\end{bmatrix}
\right)
dS \\ =
\begin{bmatrix}
\int_{S} (y-p_{y}) \sigma_{z}(x,y) dS\\
-\int_{S} (x-p_{x}) \sigma_{z}(x,y) dS\\
\int_{S}\left\{
(x-p_{x}) \sigma_{y}(x,y) - (y-p_{y}) \sigma_{x}(x,y)
\right\}dS
\end{bmatrix}
$$

を得る．これは力ベクトル$${\bm{\sigma}}$$の１次のモーメントに相当する．

ここでCOPの定義から，COPは鉛直方向の力がつくる水平軸の力のモーメントが$${0}$$となる点，すなわち分布する床反力の重心点と考えているため，$${\bm{p}_c=[p_x~p_y~0]^T}$$まわりの力のモーメント$${\bm{m}(\bm{p}_c)=[m_x~m_y~m_z]^T}$$の水平成分$${(m_x,m_y)}$$を$${0}$$とし，

$$
\int_{S} (y-p_{y}) \sigma_{z}(x,y) dS = 0,~\int_{S} (x-p_{x}) \sigma_{z}(x,y) dS = 0
$$

を解くことで，COPの座標

$$
p_{x} = \frac{\int_{S} x \sigma_{z}(x,y) dS}{\int_{S} \sigma_{z}(x,y) dS} = \frac{\int_{S} x \sigma_{z}(x,y) dS}{F_{z}}
\\
p_{y} = \frac{\int_{S} y \sigma_{z}(x,y) dS}{\int_{S} \sigma_{z}(x,y) dS} = \frac{\int_{S} y \sigma_{z}(x,y) dS}{F_{z}}
$$

を得る．この式が，「図５のグレーの塊に対して床面でバランスする重心点」としてのCOPの物理的意味を示している．

さて，COPまわりの，すなわち　COPを原点としたモーメント$${\bm{m}(\bm{p})}$$の$${x,y}$$成分は釣り合いから$${0}$$となるが，モーメントの$${z}$$成分

$$
m_z =\int_{S}\left\{ (x-p_{x}) \sigma_{y}(x,y) - (y-p_{y}) \sigma_{x}(x,y) \right\}dS
$$

は消えずに，

$$
\bm{m}(\bm{p}_c) = \begin{bmatrix} 0\\0\\m_z\end{bmatrix}
$$

となる．そして，この残った鉛直方向の力のモーメント$${\bm{m}(\bm{p})}$$は，バイオメカニクスではフリーモメント（free moment）と呼ばれるが，ここでは摩擦モーメント（frictional moment, vertical moment）と呼び，以後$${\bm{\tau}(\bm{p}_c)}$$と記述する．

なお，この$${\bm{\tau}(\bm{p}_c)=[0~0~\tau_z]^T}$$は「図５のグレーの塊をCOPの鉛直軸回りに回転させる力のモーメント」という物理的意味を持つ．

以上から，フォースプレートの表面に位置する「COPまわりでは，力のモーメントの水平成分をバランスし消えるように定義したが，鉛直成分$${\tau_z}$$だけが残って作用する」ことがわかる．

摩擦モーメントの座標変換
　次に，このことを利用して力のモーメントを，COPまわりの力のモーメントからフォースプレート座標$${\text{S}}$$へ座標変換する．この$${\text{S}}$$まわりの力のモーメント$${\bm{M}_s}$$は，平行軸の定理で$${\text{C}}$$から$${\text{S}}$$まわりのモーメントに座標変換することで，

$$
\bm{M}_s =  \begin{bmatrix} 0\\0\\\tau_z\end{bmatrix} + \left( \begin{bmatrix} p_x\\p_y\\0\end{bmatrix} + \begin{bmatrix} 0\\0\\c\end{bmatrix} \right) \times \begin{bmatrix} F_x\\ F_y\\ F_z\end{bmatrix} \\= \bm{\tau}(\bm{p}_c)+(\bm{p}_c+\bm{c}) \times \bm{F} \\= \bm{\tau}(\bm{p}_c)+ \bm{p}_s \times \bm{F}
$$

と書くことができる．ここで，$${\bm{p}_s}$$は原点$${\text{S}}$$から見たCOPの位置ベクトル，$${c}$$はフォースプレートのセンサ座標系の原点から見たフォースプレート表面までの鉛直方向の距離，$${\bm{c}=[0~0~c]^T}$$である（図９参照）．

具体的には，COPまわりの$${\bm{\tau}(\bm{p}_c)}$$に，座標系$${\text{S}}$$の原点の位置ベクトル$${\bm{p}_s = (\bm{p}_c+\bm{c})}$$と床反力$${\bm{F}}$$の外積として，移動分の力のモーメントを加算することで，$${\text{S}}$$まわりのモーメント$${\bm{M}_s}$$を計算している．平行軸の定理については補足５を参照されたい．

補足３：圧力中心と摩擦モーメントの計算

補足２では，COPと摩擦モーメントの物理的意味を述べたが，ここでは，具体的にCOPの位置ベクトル$${\bm{p}_s = [px ~py~ c]^T }$$と摩擦モーメント$${\bm{\tau}(\bm{p}_s)=[0~0~\tau_z]^T}$$を導出する．

ただし，補足２で述べた座標系$${\text{C}}$$の原点からみたCOPの位置ベクトル$${\bm{p}_c}$$は，座標系$${\text{S}}$$の原点からみると$${\bm{p}_s}$$と書けるので，以下，摩擦モーメント$${\bm{\tau}(\bm{p}_c)}$$は，座標系$${\text{S}}$$からみた摩擦モーメント$${\bm{\tau}(\bm{p}_s)}$$に置き換える．

また，ここではフォースプレート座標系$${\text{S}}$$に基づいて計算を行うが，実際の座標系の向きやパラメータなどはご使用のフォースプレートの仕様を確認されたい．

補足２の最後で述べたように，COPまわりの力のモーメント$${\bm{\tau}(\bm{p}_s)}$$を，座標系$${\text{S}}$$に平行軸の定理を用いて座標変換することで，

$$
\bm{M}_s = \bm{\tau}(\bm{p}_s) + \bm{p}_s \times \bm{F} \\ \begin{bmatrix} M_{sx}\\M_{sy}\\M_{sz} \end{bmatrix}=  \begin{bmatrix} 0\\0\\\tau_z\end{bmatrix} + \begin{bmatrix} p_x\\p_y\\c\end{bmatrix} \times \begin{bmatrix}F_x\\F_y\\F_z\end{bmatrix} \\ =  \begin{bmatrix} 0\\0\\\tau_z\end{bmatrix} + \begin{bmatrix}0 & -c & p_y\\ c & 0 & -p_x\\ -p_y & p_x & 0\end{bmatrix} \begin{bmatrix}F_x\\F_y\\F_z\end{bmatrix} \\= \begin{bmatrix} -c F_y + p_y F_z\\ c F_x - p_x F_z\\ \tau_z - p_y F_x + p_x F_y \end{bmatrix}
$$

のように，フォースプレートの力のモーメントの出力$${\bm{M}_s}$$を，COPの位置ベクトル$${\bm{p}_s}$$，床反力$${\bm{F}}$$，摩擦モーメント$${\bm{\tau}(\bm{p}_s)}$$で置き換えることができるので，COPの位置ベクトル$${\bm{p}_s}$$

$$
\bm{p}_{s}= \begin{bmatrix} p_{x}\\p_{y}\\c \end{bmatrix} = \begin{bmatrix} \frac{-M_{sy}+c F_{x}}{F_{z}}\\ \frac{M_{sx}+c F_{y}}{F_{z}} \\c \end{bmatrix}
$$

と，摩擦モーメント$${\bm{\tau}(\bm{p}_s)}$$

$$
\bm{\tau}(\bm{p}_s) = \begin{bmatrix} 0 \\ 0 \\ \tau_{z} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ M_{sz} + p_{y} F_{x} - p_{x} F_{y} \end{bmatrix}
$$

を得る．これらの計算には，フォースプレートの出力である力$${\bm{F}}$$と力のモーメント$${\bm{M}_s}$$の他に，センサの座標系からフォースプレート表面までの鉛直方向の距離パラメータ$${c}$$が必要となることに注意されたい．

補足４：Kistler社のフォースプレートの出力と力のモーメント

図９に示したフォースプレートの各力覚センサの出力を

$$
\bm{f}_{1} = \begin{bmatrix} f_{1x}\\f_{1y}\\f_{1z} \end{bmatrix}, ~ \bm{f}_{2} = \begin{bmatrix} f_{2x}\\f_{2y}\\f_{2z} \end{bmatrix}, ~ \bm{f}_{3} = \begin{bmatrix} f_{3x}\\f_{3y}\\f_{3z} \end{bmatrix}, ~\bm{f}_{4} = \begin{bmatrix} f_{4x}\\f_{4y}\\f_{4z} \end{bmatrix}
$$

とする．

多くのフォースプレートは，これらをまとめた，力$${\bm{F}=\bm{f}_1+\bm{f}_2+\bm{f}_3+\bm{f}_4=[F_x~F_y~F_z]^T}$$と力のモーメント$${\bm{M}_s=[M_{sx}~M_{sy}~M_{sz}]^T}$$を出力するが，Kistler社のフォースプレートは，力のモーメントを出力せず，図９に示したフォースプレートの各$${z}$$方向の力$${(f_{z1},f_{z2},f_{z3},f_{z4})}$$と，$${x}$$方向の力$${f_{x12} = f_{1x}+f_{2x}, ~f_{x34}=f_{3x}+f_{4x}}$$と，$${y}$$方向の力$${f_{y14}=f_{1y}+f_{4y},~ f_{y23} = f_{2y}+f_{3y}}$$を出力する．したがってKistler社のフォースプレートの力のモーメントの計算には，センサの座標系から力覚センサまでの距離パラメータ$${a,b}$$が必要となることに注意されたい．

図９に示すように，座標系$${\text{S}}$$の原点から各センサまでの$${x,y,z}$$軸における距離が$${a, b, c}$$ならば，原点から各センサまでの各位置ベクトル$${\bm{r}_{sj}}$$は

$$
\bm{r}_{s1} = \begin{bmatrix} -a\\b\\0 \end{bmatrix}, ~ \bm{r}_{s2} = \begin{bmatrix} a\\b\\0 \end{bmatrix}, ~ \bm{r}_{s3} = \begin{bmatrix} a\\-b\\0 \end{bmatrix}, ~\bm{r}_{s4} = \begin{bmatrix} -a\\-b\\0 \end{bmatrix}
$$

で与えられるので，センサ座標系$${\text{S}}$$の原点まわりの力のモーメント$${\bm{m}_{s}}$$は，

$$
\bm{M}_{s} = \begin{bmatrix} M_{sx}\\M_{sy}\\M_{sz} \end{bmatrix} = \begin{bmatrix} b (f_{1z}+f_{2z}-f_{3z}-f_{4z}) \\ - a (-f_{1z}+f_{2z}+f_{3z}-f_{4z}) \\ -b (f_{1x}+f_{2x}-f_{3x} -f_{4x}) + a(-f_{1y}+f_{2y}+f_{3y}-f_{4y}) \end{bmatrix}
$$

から計算することができる．

補足５：平行軸の定理

ある軸回りの慣性モーメントを計測し，さらに平行移動した別の軸回りの慣性モーメントを計算するときに平行軸の定理（parallel axis theorem）が用いられる．したがって，この定理は慣性モーメントの計算にしか適用できないと考えている方も多いかもしれない．しかし，これはモーメント全般に成り立つ定理である．

力のモーメントは，ベクトルのモーメントで，束縛ベクトルである．すなわち，座標系の原点が異なればそのモーメントの値も異なる．

では，ある座標系からみた「ベクトルのモーメント」を，異なる座標系に平行移動した際の新しいモーメントをどのように計算したら良いのであろうか？ちなみに，慣性モーメントのような「スカラ値のモーメント」でも基本的には考え方は同じである．

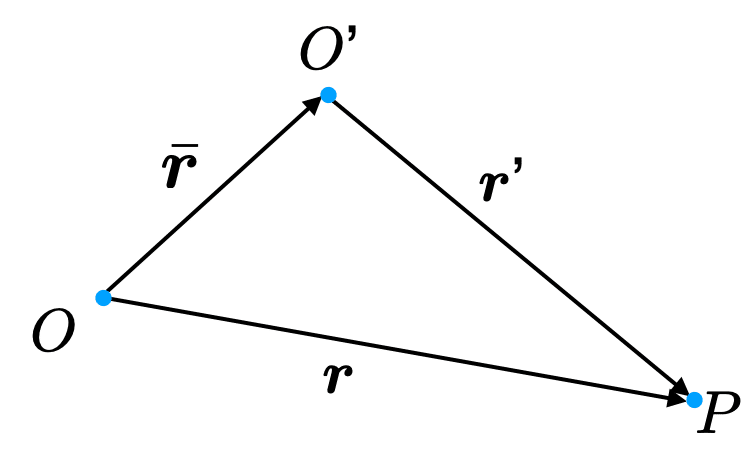
原点$${\text{O}}$$からみた点$${P}$$の位置ベクトルを$${\bm{r}}$$とし，原点$${\text{O}}$$まわりの$${\bm{B}}$$のモーメントを$${\bm{M}(O)\equiv \bm{r} \times \bm{B}}$$とする．また同様に，別の始点$${\text{O'}}$$からみた点$${P}$$の位置ベクトルを$${\bm{r}'}$$とし，$${\text{O}'}$$まわりのベクトル$${\bm{B}}$$のモーメントを$${\bm{M}(\text{O}') \equiv \bm{r}' \times \bm{B}}$$とする．

このとき，

$$
\bm{r} = \bm{r}^{\prime}+\bar{\bm{r}}
$$

とすると，

$$
\bm{r} \times \bm{B} = \bm{r} ^{\prime} \times \bm{B} + \bar{\bm{r}} \times \bm{B}
$$

が成り立つので，

$$
\bm{M}(\text{O}) = \bm{M}(\text{O}^{\prime}) + \bar{\bm{r}} \times \bm{B}
$$

が成立する．すなわち，ある始点まわりのモーメント$${\bm{M}(\text{O}^{\prime})}$$，モーメントを計算するためのベクトル$${\bm{B}}$$，別な始点の位置関係$${\bar{\bm{r}}}$$がわかれば，新しい座標系のモーメント$${\bm{M}(\text{O}^{\prime})}$$も，計算できることを示している．このことは，平行軸の定理が慣性モーメントだけに成り立つのではなく，力のモーメントや角運動量ベクトルに関しても成立することを示している．

例えば，他のベクトルのモーメントである角運動量ベクトルでもこの定理が成立するが，スカラの２次のモーメントである慣性モーメントに関する平行軸の定理は，多くの教科書に取り上げられているので，それらを参照されるとよい．

補足６：自由ベクトルと束縛ベクトル

ここで自由ベクトルと束縛ベクトルについて，補足７で偶力について整理をしておく．

数学におけるベクトルは，単に大きさと方向を定めたベクトルであって，始点Aと終点Bを定めて有向線分的にベクトルを$${\overrightarrow{\text{AB}}}$$と定めても，同じ大きさと同じ方向を持つ別のベクトル$${\overrightarrow{\text{CD}}}$$との区別はされず，それらは同じベクトルとみなされる．すなわち始点はどこにあっても同じ大きさと方向を持てば，それは同じベクトルとみなされる．

ところが，物理では，始点に依存して値が異なるベクトルがあり，ここで取り上げた力のモーメントベクトルも座標系の原点（回転の中心）に依存して値が異なる．たとえば，フォースプレートは４つの力覚センサの出力から計算する，４つの力のモーメントの和であるが，これらは原点（始点）の選択の仕方で値が異なることは，自分で計算を行ってみればすぐに分かるだろう．この他，位置ベクトルも始点に依存する．このような，始点や座標系の選択の仕方に依存したベクトルを束縛ベクトル（bound vector）と呼ぶ．

一方，速度ベクトルや加速度ベクトルは位置ベクトルの微分で記述できるが，原点や始点の選択に依存せず，位置ベクトルの始点と独立に決まる．このようなベクトルを自由ベクトル（free vector）と呼び，平行移動して構わないベクトルと言える．次に述べる偶力による力のモーメントも自由ベクトルである．

補足７：偶力

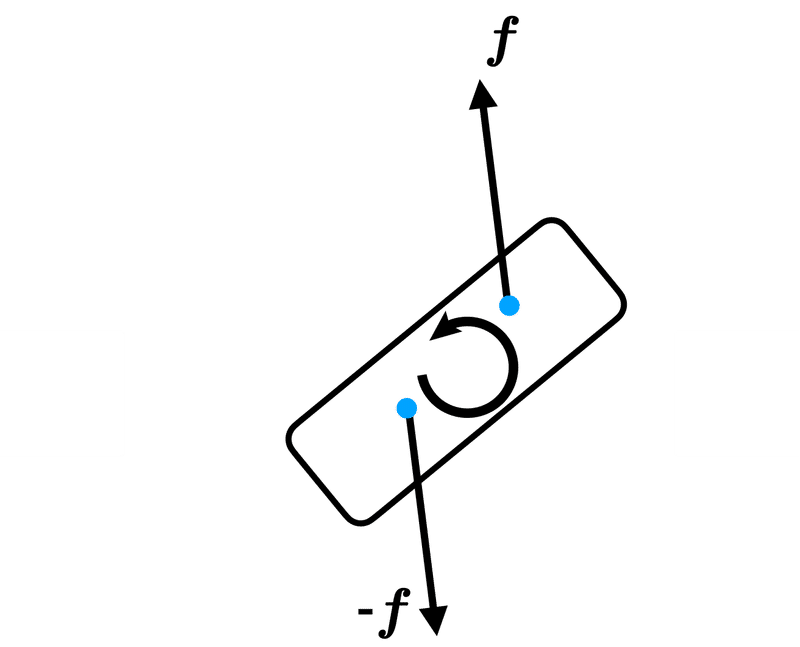
複数の力が異なる位置に作用する際，その力によって力のモーメントが生じることがある．このうち，図11に示したように，反対向きで同じ大きさの力の組み合わせを偶力（force couple）と呼ぶ．ただし，これらの力は，異なる直線上に並び，異なる場所に作用する必要がある．

ここで偶力を$${\bm{f}, -\bm{f}}$$とすると， 偶力の合力は$${\bm{f}+(-\bm{f})=\bm{0}}$$なので，偶力には物体を移動させるはたらきがない．しかし，偶力は力のモーメントをうみ物体を回転させるはたらきがあることがわかる（図11参照）．

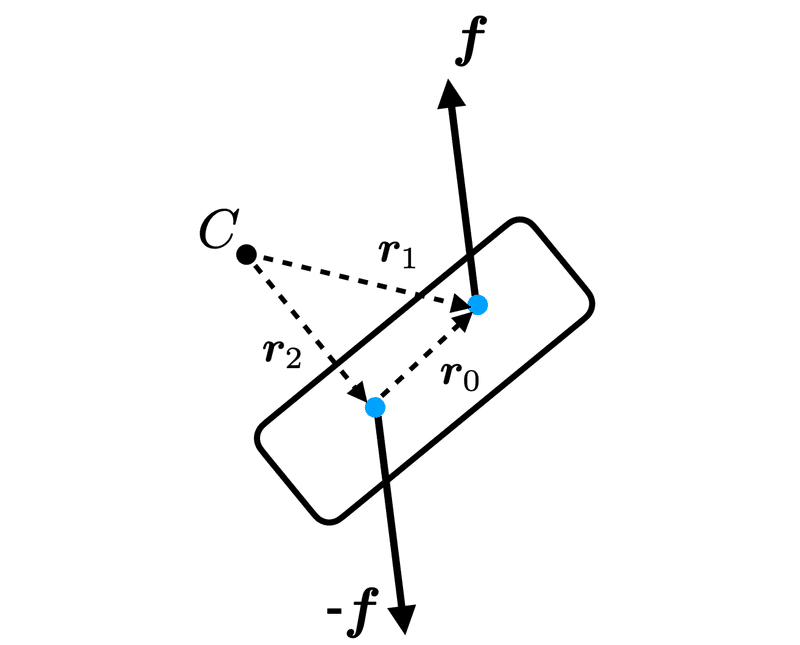
図12に示す偶力が作る力のモーメントを考えると，点$${C}$$から見た偶力$${\bm{f}, -\bm{f}}$$による力のモーメントは

$$
\bm{r}_1 \times \bm{f} + \bm{r}_2 \times (-\bm{f}) = (\bm{r}_2 + \bm{r}_0) \times \bm{f} + \bm{r}_2 \times (-\bm{f}) = \bm{r}_0 \times \bm{f}
$$

のように，どこを回転の中心（座標系の原点）として選択しても，常に偶力間の位置ベクトル$${\bm{r}_0}$$と偶力の外積で計算されることから，偶力が作る力のモーメントは座標系（回転の中心）と無関係に決まる．通常，力のモーメントは座標系の原点に依存して変わる束縛ベクトルであるが，偶力が作る力のモーメントは特別で，自由ベクトルとなる．

補足８：フリーモーメント

一般に力のモーメントは回転の中心（座標系の原点）からの距離に依存して変化する束縛ベクトルである．ただし，力のモーメントが自由ベクトルとなる特別な場合として，偶力による力のモーメントを補足７で述べた．

定義から，作用する力の総和が０となる場合に偶力となるが，力がフォースプレートに作用している間，床反力の水平成分の合力（前述の$${F_x = \int \sigma_x (x,y) dS, F_y = \int \sigma_y (x,y) dS}$$はどちらも$${0}$$でないので，床反力の水平成分は偶力ではなく，これによりCOPまわりの力のモーメント$${\bm{\tau}(\bm{p})}$$は束縛ベクトルとなる．

たとえば，図12(a)のようにフォースプレート表面に対して後方に足をするように蹴るならば，水平力分布は前方に偏り，その合力は$${0}$$にはならず偶力は含まれない．

図12(b)のように足をひねるように摩擦を与えても，偶力として打ち消し合う力を含むため，図12(a)と比べて水平力の合力は小さくなるだろうが，決して$${0}$$にはならない．この場合の床反力の水平成分は，偶力と合力の和で表される．

このことを考えれば，鉛直方向も含めて床反力に作用する力のモーメントは，偶力を含まないこともあるし，偶力を含むことはあっても偶力によるモーメントではない．したがって，力のモーメント$${\bm{\tau}(\bm{p})}$$は，COPの位置$${\bm{p}}$$に依存して変化するベクトルで，自由ベクトルではない．

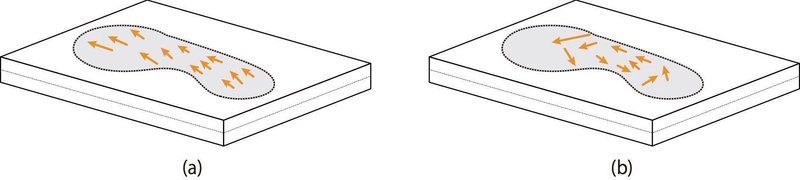
ところが，多くの文献で$${\bm{\tau}(\bm{p})}$$が偶力による力のモーメントと等価になると解釈し，バイオメカニクスではこの$${\bm{\tau}(\bm{p})}$$をフリーモーメント（free moment）と呼んでいる．しかし，ここで確かめたように$${\bm{\tau}(\bm{p})}$$は偶力を含むことはあっても，偶力による力のモーメント，すなわち束縛ベクトルにはならず，この名称は誤用と思われる．この件に関しては現在，文献をたどり調査中である．

このような理由から，ここでは$${\bm{\tau}(\bm{p})}$$をフリーモーメントとは呼ばず，摩擦モーメントと呼んでいる．摩擦モーメントは鉛直摩擦モーメントなどとも呼ばれる．

補足９：力のモーメントとトルク

偶力による力のモーメントは，座標系の原点，すなわち回転の中心を変更しても，一定のベクトルを保つ自由ベクトルであることを補足７で述べた．

偶力のように作用する全ての合力が$${0}$$となる力が生成する力のモーメントを特にトルク（torque）と呼び，トルクと力のモーメントを区別することがある．

この定義によれば，たとえば，モータによって与えられる回転力はトルクである．モータの重さによる効果を除けば，モータ自体は物体に並進力を与えない．そこで，モータに作用する力は偶力が作用していると考えても良い．したがって，モータの回転力が作用している物体には，自由ベクトルとしての，つまり回転中心と独立に決まる回転力が作用している．

ただし，トルクと力のモーメントが同義に用いられることのほうが多いようだ．

補足10：座標系

冒頭で説明したように，本章での説明ではバイオメカニクスの解析を意識し，身体に作用する力として床反力を記述し，使用している座標系も解析用の座標系で記述している．具体的には$${z}$$軸が鉛直上向きの座標系である．一方，多くのフォースプレートメーカは，$${z}$$軸が鉛直下向きのフォースプレート座標系を採用し，床反力はフォースプレートに作用する力として記述される（図13参照）．これが解析の際に問題を引き起こすので注意をされたい．

なお，本章で扱った多くの式は，幾何ベクトルで記述し（たとえば，$${\bm{F}, \bm{M}_s}$$のようにイタリック・ボールドで記述された式），座標系のとり方に依存せず成り立つ．しかし，COPや，Kistlerのフォースプレートで扱った式などでは成分表示したものもあり，それらは座標系のとり方に依存する．計算するときは，ご利用のメーカーのフォースプレートの座標系を確認されたい．

また，実際にバイオメカニクスの解析を行う場合は，各メーカーのフォースプレート座標系から，身体側の座標系である解析用座標系に変換する必要がある．

その際には，まず座標系を

$$
x \rightarrow -x \\ y \rightarrow y \\ z \rightarrow -z
$$

のように$${x,z}$$軸を反転し，力と力のモーメントについては

$$
F_x \rightarrow F_x \\ F_y \rightarrow -F_y \\ F_z \rightarrow F_z
$$

$$
M_{sx} \rightarrow M_{sx} \\ M_{sy} \rightarrow -M_{sy} \\ M_{sz} \rightarrow M_{sz}
$$

のように$${y}$$軸を反転する必要がある．

また，フォースプレート座標系から見たCOPは，解析用座標系と向きが異なり，特に鉛直方向の向きが上下反転していることから，$${\bm{p}_s}$$におけるパラメータ$${c}$$に関連する符号が反転し，

$$
\bm{p}_s= \begin{bmatrix} p_{x}\\p_{y}\\-c \end{bmatrix} = \begin{bmatrix} \frac{-M_{sy}-c F_{x}}{F_{z}}\\ \frac{M_{sx}-c F_{y}}{F_{z}} \\-c \end{bmatrix}
$$

となるので注意されたい．Kistler社は$${c}$$を負の値として使用するなど，メーカによって微妙な違いも多いので，使用するフォースプレートの仕様をよく確認されたい．

参考文献

１）ヒューマノイドロボット（改訂２版），梶田秀司編著，オーム社

【解析・受託開発について】

スポーツセンシングでは，豊富な知見を持つ，研究者や各種エンジニアが研究・開発のお手伝いをしております．研究・開発でお困りの方は，ぜひスポーツセンシングにご相談ください． 
【例】
　・データ解析の代行
　・受託開発
　　（ハードウェア、組込みソフトウェア、PC/モバイルアプリ）
　・測定システム構築に関するコンサルティング　など
その他，幅広い分野をカバーしておりますので，まずはお気軽にお問い合わせください．

株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com