前回（本シリーズ (28)）では『集合』と『群』を説明しました。ここでは『部分集合』と『部分群』について解説していきます。

　前回、３次置換全体の集合
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
は、置換の積（合成）という演算に関して群となることを解説しました。この集合 $${S_3}$$ を『３次対称群』といいます。

（再掲）３次対称群の要素

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I=id(=\rho_1)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)
=\rho_2\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
=\rho_3
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}=\tau_1\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}=\tau_2\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}=\tau_3
\end{rcases}奇置換
\end{align*}
$$

　これらを三角形の図形の移動でとらえると

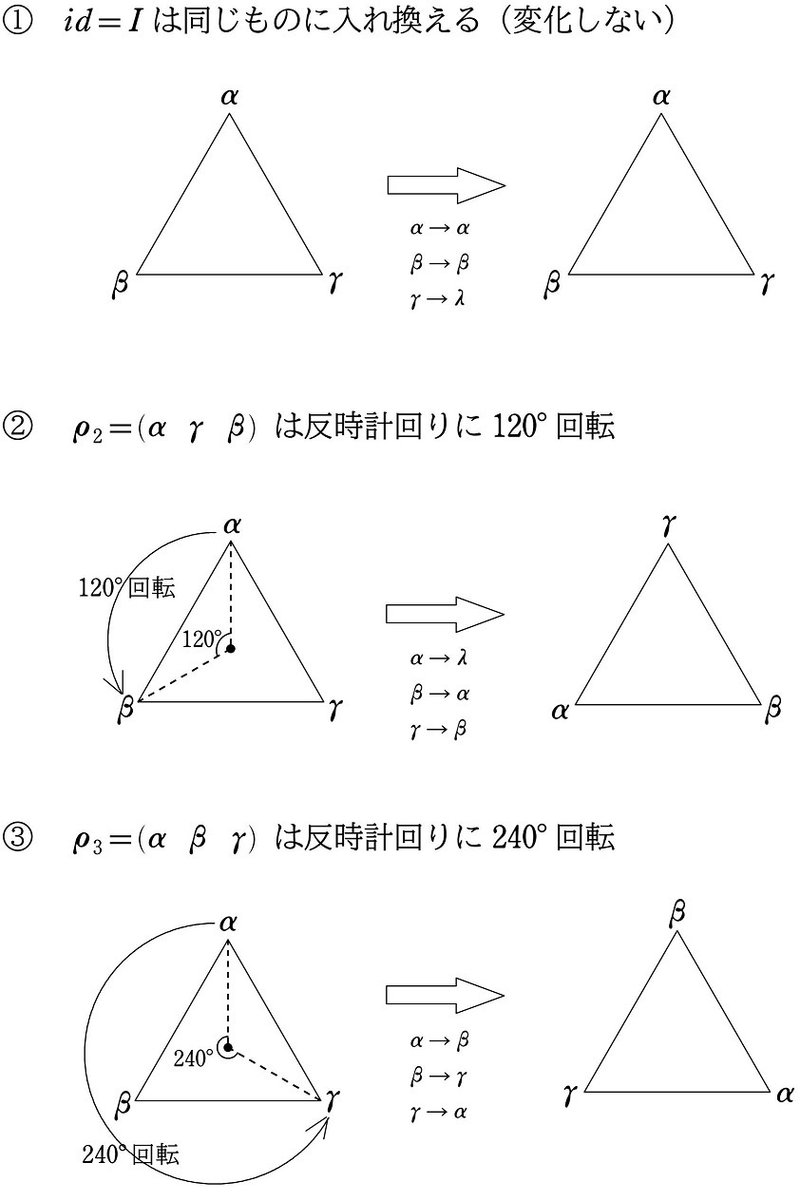
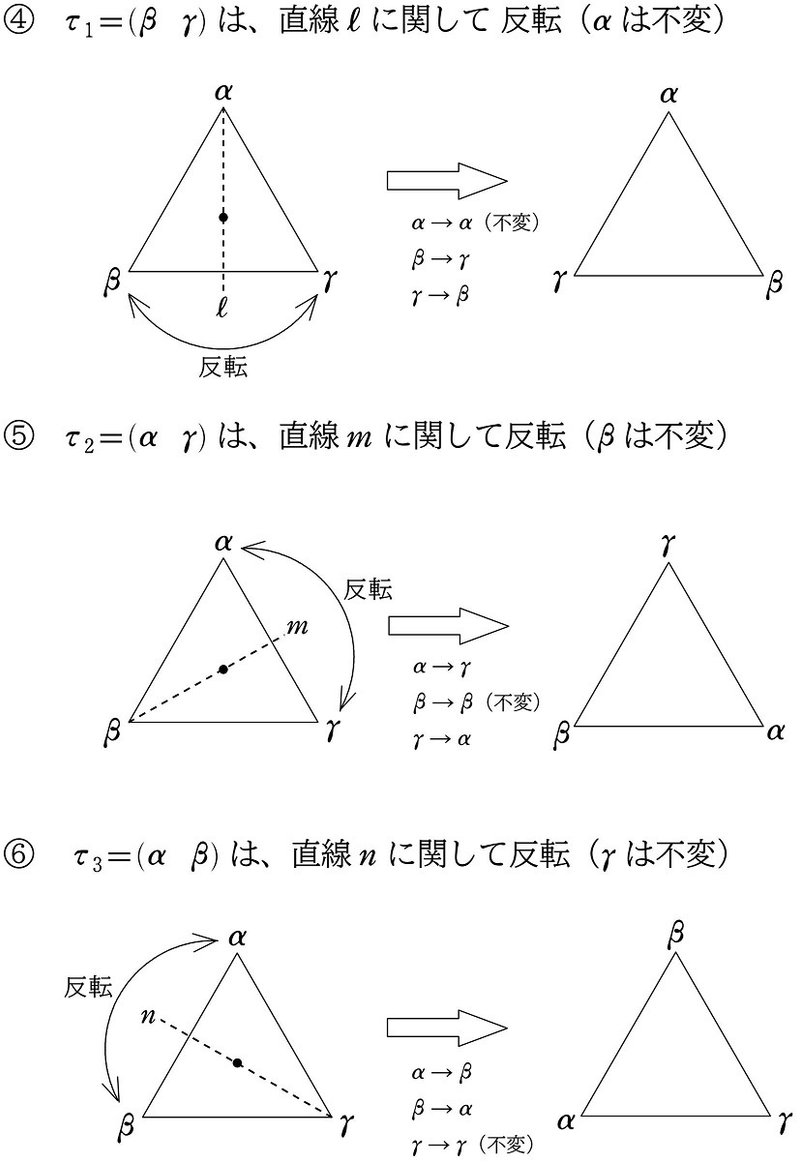
　①～③は回転、④～➅は反転と、２つに分けることができます。　
　ここからは『部分集合』、『部分群』について解説していきます。

部分集合について

　例えば、２つの集合
　$${\text{P}=\{2,  4\}}$$
　$${\text{Q}=\{1,  2,  3,  4,  5\}}$$
では、どの P の要素もまた Q の要素になっています。つまり
　P の要素 $${2}$$ は Q の要素になっている。
　P の要素 $${4}$$ は Q の要素になっている。
　この２つの集合の関係を図で描くと、次のようになります。

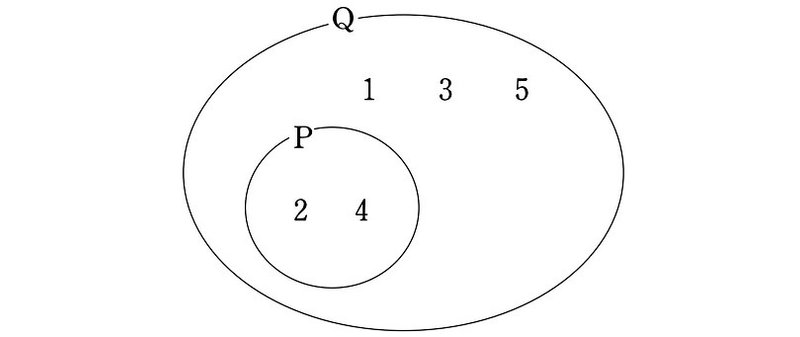
　このように、集合が表す範囲を視覚的に表したものを『ベン図』といいます。
　一般に、２つの集合 A、B において、A のどの要素もまた B の要素であるとき、すなわち

$$
\begin{align*}
x \in\text{A}　ならば　x \in\text{B}
\end{align*}
$$

が成り立つとき、A は B に含まれる、または B は A を含むといいます。

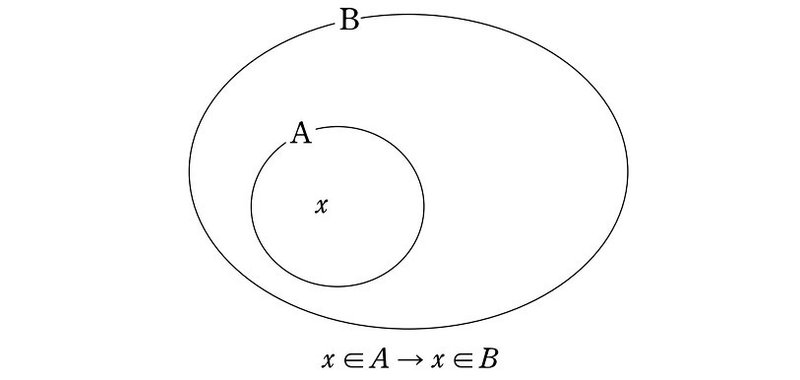
　また、A が B に含まれることを、記号で次のように書きます。

$$
\begin{align*}
\text{A}\subset\text{B}　または　\text{B}\supset\text{A}
\end{align*}
$$

このとき、$${A}$$ は $${B}$$  の『部分集合』といいます。大きい方に開いていると覚えます。２つの集合の一方が他方の部分集合であるとき、この２つの集合の間に包含関係があるといいます。

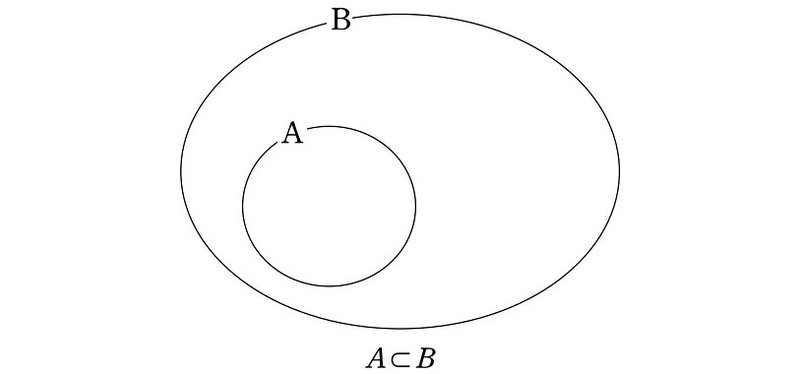
　先ほどの集合
　$${\text{P}=\{2,  4\}}$$
　$${\text{Q}=\{1,  2,  3,  4,  5\}}$$
の例でいえば、P は Q に含まれるので

$$
\begin{align*}
\text{P}\subset\text{Q}　または　\text{Q}\supset\text{P}
\end{align*}
$$

が成り立ちます。

（再掲）

　なお、同じ集合 A に対して

$$
\begin{align*}
x \in\text{A}　ならば　x \in\text{A}
\end{align*}
$$

が成り立つので、A 自身も A の部分集合、つまり

$$
\begin{align*}
\text{A}\subset\text{A}　または　\text{A}\supset\text{A}
\end{align*}
$$

となります。また、$${\text{A}\subset\text{B}}$$ かつ $${\text{B}\subset\text{A}}$$ ならば、A と B はその要素がまったく一致して

$$
\begin{align*}
\text{A}=\text{B}
\end{align*}
$$

となります。

　さて、整数全体の集合 $${\mathbb{Z}}$$ を要素を並べて書くと、次のようになります。

$$
\begin{align*}
\mathbb{Z}=\{\cdots,  -3.  -2.  -1,   0,   1,   2,   3,  \cdots\}
\end{align*}
$$

　ここで、自然数全体の集合を $${\mathbb{N}}$$ を考えます。要素を並べて書くと次のようになります。

$$
\begin{align*}
\mathbb{N}=\{1,   2,   3,   4,   5,  \cdots\}
\end{align*}
$$

記号 $${\mathbb{N}}$$ は、Natural number（自然数）の頭文字からきています。
　すると、集合 $${\mathbb{N}}$$ は、集合 $${\mathbb{Z}}$$ に含まれていることがわかります。つまり

$$
\begin{align*}
\mathbb{N}\subset\mathbb{Z}
\end{align*}
$$

　ベン図で表すと次のようになります。

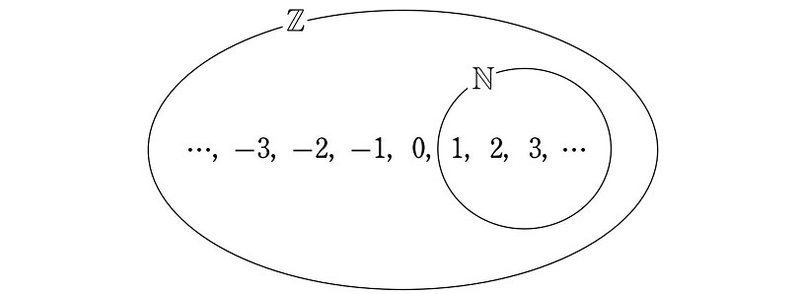
　つまり、集合 $${\mathbb{N}}$$ は、集合 $${\mathbb{Z}}$$ の部分集合です。集合 $${\mathbb{N}}$$ は、集合 $${\mathbb{Z}}$$ に含まれるという包含関係があります。

集合 {1,  2,  3} のすべての部分集合

　ここで、集合 $${\{1,  2,  3\}}$$ のすべての部分集合を考えてみましょう。以下の集合が $${\{1,  2,  3\}}$$ の部分集合になります。
　$${\phi}$$、$${\{1\}}$$、$${\{2\}}$$、$${\{3\}}$$、
　$${\{1,  2\}}$$、$${\{1,  3\}}$$、$${\{2,  3\}}$$、$${\{1,  2,  3\}}$$
　$${\phi}$$（ファイ）は空集合を表します。空集合は要素をまったくもたない集合です。空集合 $${\phi}$$ は、どのような集合の部分集合にもなっていると考えます。また、自分自身も部分集合となるので、$${\{1,  2,  3\}}$$ も部分集合です。

　さて、整数全体の集合 $${\mathbb{Z}}$$ は、たし算に関して群となることは前回示しました。では、その部分集合である $${\mathbb{N}}$$ も、たし算に関して群になるでしょうか？　前回述べた群の定義 (1)～(4) を満たすかどうかで確認していきます。
　まずは。前回やった群の定義の復習です。

群の定義（復習）

　空でない集合 $${G}$$ の任意の要素 $${a,  b,  c}$$ の間に１つの演算 $${*}$$ が規定されているとする。
　この集合 $${G}$$ の任意の要素 $${a,  b,  c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1)　$${a*b}$$ は $${G}$$ の要素である。
(2)　交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3)　$${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4)　$${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。

＊＊＊

(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。その要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元になるような要素の存在です。その要素を逆元といいます。

　要するに群とは、イメージとして
(1)　全部そろっている
(2)　つなげることができる
(3)　変えないことができる
(4)　元に戻すことができる
の４つの条件が成り立つもの（要素）の集まり（集合）です。

部分群とは

　ある群 $${G}$$ の空でない部分集合 $${H}$$ が同じ演算で群になるとき、その部分集合 $${H}$$ を、 $${G}$$ の『部分群』といいます。
　ここで重要なのは、あくまでも「同じ演算で」ということです。もとの群がたし算に関して群となる場合、その部分群もたし算に関して群となります。

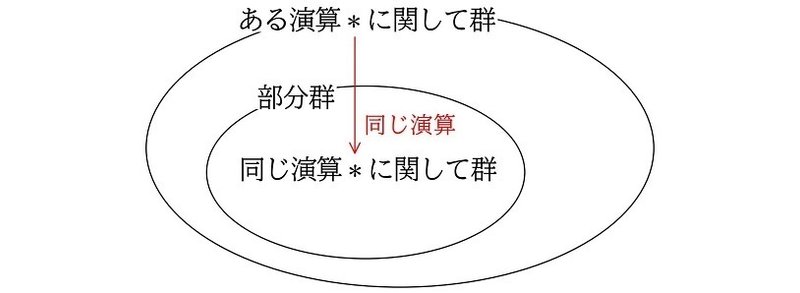
たし算に関してℕはℤの部分群か？

　さて、整数全体の集合

$$
\begin{align*}
\mathbb{Z}=\{\cdots,  -3.  -2.  -1,   0,   1,   2,   3,  \cdots\}
\end{align*}
$$

は、たし算に関して群となることは前回示しました。では、その部分集合である自然数の集合

$$
\begin{align*}
\mathbb{N}=\{1,   2,   3,   4,   5,  \cdots\}
\end{align*}
$$

は部分群になるでしょうか。もちろん部分群は「同じ演算」で考えるので、考える演算はたし算です。
　では、群の定義 (1)～(4) を順に確認していきます。

(1)　自然数同士を足しても自然数である。
　$${2+3=5}$$（自然数）
　自然数はたし算について閉じています。

(2)　結合法則は成り立つ。
例　$${(2+3)+5=2+(3+5)}$$
　結合法則は常になりたちます。

しかし・・・

(3)　単位元は存在しない。
　足しても変化しないのが単位元です。例えば
　$${1+e=e+1=1}$$
を考えます。$${1}$$ に足しても変化しないもの、これ満たす $${e}$$ が単位元となりますが、それは自然数の集合には存在しません。計算上では $${e=0}$$ とすれば成り立ちますが、$${0}$$ は自然数ではないので、(3) は満たさないことが分かります。
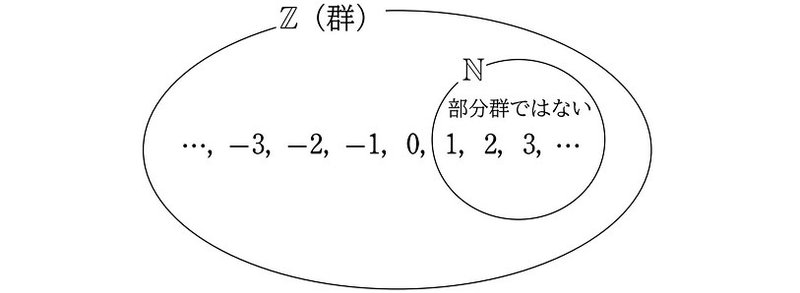
　よって (3) を満たさない（つまり、(1)～(4) のすべてを満たさない）ので、$${\mathbb{N}}$$ はたし算に関して $${Z}$$ の部分群にならないことが示されました。

たし算に関して {-1, 0, 1} はℤの部分群か？

　一方、 $${\mathbb{Z}}$$ の部分集合として
　$${S=\{-1,  0,  1\}}$$
をとったとき、この集合 $${S}$$ はたし算に関して群になるでしょうか。群の定義 (1)～(4) を順に確認していきます。

(1)　$${S}$$ の任意の要素同士を足しても $${S}$$ の要素になる。
　すべての要素について確認します。
　$${-1+0=-1 \in S}$$
　$${0+(-1)=-1 \in S}$$
　$${-1+1=0 \in S}$$
　$${1+(-1)=0 \in S}$$
　$${0+1=1 \in S}$$
　$${1+0=1 \in S}$$
より、足したものはすべて $${S}$$ の要素になります。$${S}$$ はたし算について閉じています。

(2)　結合法則は成り立つ。
例　$${(-1+0)+1=-1+(0+1)}$$
　結合法則は常に成り立ちます。

(3)　単位元は存在する。
　足しても変化しないのが単位元です。
　$${-1+\underline{0}=\underline{0}+(-1)=-1}$$（変化しない）
　$${\hspace{8pt}0+\underline{0}=\underline{0}+0=0}$$（変化しない）
　$${\hspace{8pt}1+\underline{0}=\underline{0}+1=1}$$（変化しない）
より、下線部の $${0}$$ が単位元となります。よって、単位元は $${S}$$ に存在します。

(4)　逆元は存在する。
　たして単位元 $${0}$$ になるのが逆元です。
　$${-1+\underline{1}=\underline{1}+(-1)=0}$$（単位元）
より、$${-1}$$ の逆元は $${1}$$
　$${0+\underline{0}=\underline{0}+0=0}$$（単位元）
より、$${0}$$ の逆元は $${0}$$
　$${1+(\underline{-1})=\underline{-1}+1=0}$$（単位元）
より、$${1}$$ の逆元は $${-1}$$
　下線部が各々の逆元です。よって、すべての要素に対して逆元は $${S}$$ に存在します。

　以上により、群の条件 (1)～(4) をすべて満たしているので
　$${S=\{-1,  0   1\}}$$
は、たし算に関して $${Z}$$ の部分群となります。
　 $${N}$$ も $${S}$$ も $${Z}$$ の部分集合ではありますが、たし算に関して、$${N}$$ は部分群ではなく $${S}$$ は部分群となります。

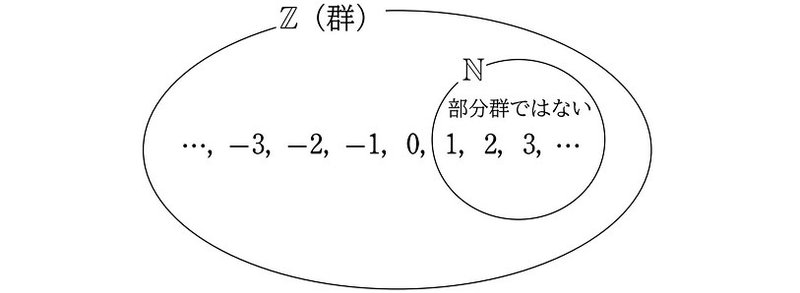
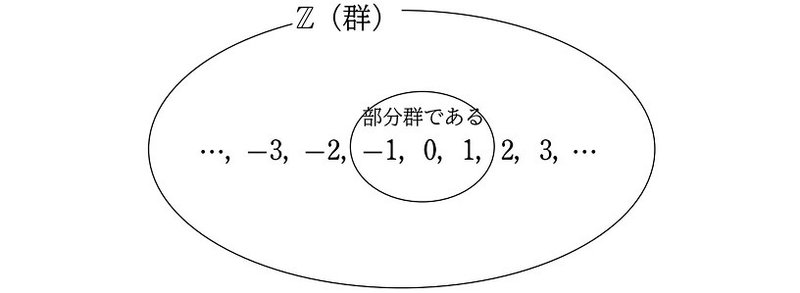
　部分集合であっても、部分群となる場合もあれば、ならない場合もあります。
　ここで部分群について補足です。
　ある群 $${G}$$ の部分群のうち、最大のものは自分自身 $${G}$$ です。また、最小のものは単位元 $${e}$$ だけからなる群 $${\{e\}}$$ です（注１）。この２つは『自明な部分群』といいます。どんな群にも、この自明な部分群は必ず存在します。自明な部分群以外の部分群を『真部分群』といいます。真部分群があるかないかは群によります。

３次交代群について

　さて、３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
は置換の積に関して群となりますが、その遇置換だけを集めた部分集合
　$${A_3=\{id,  \rho_2,  \rho_3\}}$$
は、$${S_3}$$ の部分群となるでしょうか。結論からいうと、$${A_3}$$ は $${S_3}$$ の部分群となります。この $${A_3}$$ を『３次交代群』といいます。

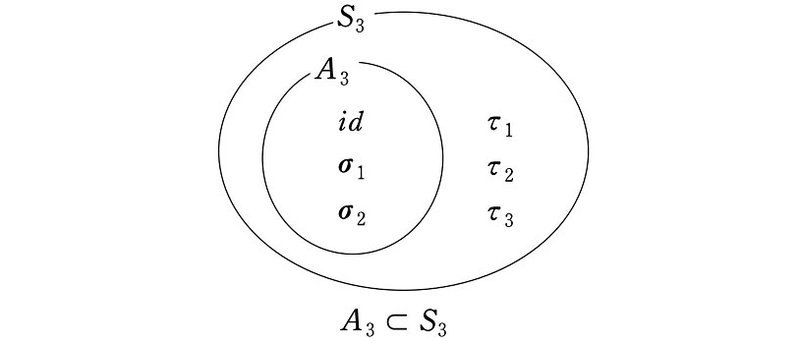
　では、この遇置換だけを集めた３次交代群 $${A_3}$$ が、置換の積に関して群の定義 (1)～(4) を満たしていることを確認していきます。

遇置換の集合が部分群になることの証明

(1)　遇置換同士の積は遇置換である。

　$${A_3}$$ の任意の２つの要素の積は $${A_3}$$ の要素になります。
　$${A_3}$$ の要素は全部で $${3}$$ 通りあるので、その置換の積は全部で $${3\times3=9}$$ 通りありますが、そのすべてが $${A_3}$$ の要素になること、つまり $${A_3}$$ からはみ出さないことを具体的に示していきます。
　前回 $${S_3}$$ に対して行ったのと同じ方法なので、ここでは簡潔に書いていきます。

(a)　先に $${id}$$ を作用させると、結果は次のようになります。$${id}$$ は恒等置換なので、いずれも変化しません。
(a1)　$${idid=id}$$
(a2)　$${id\rho_2=\rho_2}$$
(a3)　$${id\rho_3=\rho_3}$$

　(a1)～(a3) は、すべて $${A_3}$$ の要素になります。
　この結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{0pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
    & id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3
\end{array}
\begin{array}{c}
\\
← \text{(a)}
\end{array}
$$

(b)　先に $${\rho_2}$$ を作用させると、結果は次のようになります。
(b1)　$${\rho_2id=\rho_2}$$
(b2)　$${\rho_2\rho_2=\rho_3}$$
(b3)　$${\rho_2\rho_3=id}$$

　(b1)～(b3) は、すべて $${A_3}$$ の要素になります。
　これまでの結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{0pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
    & id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id
\end{array}
\begin{array}{c}
\\
← \text{(a)}\\
← \text{(b)}
\end{array}
$$

(c)　先に $${\rho_3}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。
(c1)　$${\rho_3id=\rho_3}$$
(c2)　$${\rho_3\rho_2=id}$$
(c3)　$${\rho_3\rho_3=\rho_2}$$

　(c1)～(c3) は、すべて $${A_3}$$ の要素になります。
　これまで結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{0pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c}
    & id & \rho_2 & \rho_3\\ \hline\hline
id & id & \rho_2 & \rho_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id &\\ \hline
\rho_3 & \rho_3 & id & \rho_2
\end{array}
\begin{array}{c}
\\
\leftarrow (a)\\
\leftarrow (b)\\
\leftarrow (c)
\end{array}
$$

　以上により、$${3\times3=9}$$ 通りのすべてが $${A_3}$$ の要素に含まれることが分かりました。$${A_3}$$ は置換の積について閉じています。

(2)　結合法則は成り立つ。

例　$${(\rho_2id)\rho_3=\rho_2(id\rho_3)}$$
　　$${(\rho_2id)\rho_2=\rho_2(id\rho_2)}$$
　任意の要素に対して成り立つので、同じ要素があっても構いません。
　結合法則は常に成り立ちます。

(3)　単位元は存在する。

　置換の積で、変化しないのが単位元です。
　$${id\underline{id}=\underline{id}id=id}$$（変化しない）
　$${\rho_2\underline{id}=\underline{id}\rho_2=\rho_2}$$（変化しない）
　$${\rho_3\underline{id}=\underline{id}\rho_3=\rho_3}$$（変化しない）
より、下線部の $${id}$$ が単位元となります。よって、単位元は $${A_3}$$ に存在します。

(4)　逆元は存在する。

　置換の積で、単位元 $${id}$$ になるのが逆元です。
　$${id}$$ については
　$${id\underline{id}=\underline{id}id=id}$$（単位元）
より、$${id}$$ が逆元となります。
　$${\rho_2}$$ については
　$${\rho_2\underline{\rho_3}=\underline{\rho_3}\rho_2=id}$$（単位元）
より、$${\rho_3}$$ が逆元となります。
　$${\rho_3}$$ については
　$${\rho_3\underline{\rho_2}=\underline{\rho_2}\rho_3=id}$$（単位元）
より、$${\rho_2}$$ が逆元となります。
　下線部が各々の逆元です。よって、すべての要素に対して逆元は $${A_3}$$ に存在します。
　置換を回転とみなすと、$${\rho_2}$$ は $${120^\circ}$$ 回転、$${\rho_3}$$ は $${240^\circ}$$ 回転なので、それらを連続して回転させると $${360^\circ}$$ になり、元に戻る（$${id}$$ になる）というイメージです。

　以上により、群の定義 (1)～(4) をすべて満たしているので、$${A_3}$$ は置換の積に関して群となります。そしてそれは $${S_3}$$ の部分集合であることから、$${A_3}$$ は $${S_3}$$ の部分群となることが示されました。

３次対称群のすべての部分群

　先ほど示したのも含めて、置換の積に関して
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
の部分群になるものには、全部で以下の６通りがあります。
　$${\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}=S_3}$$
　$${\{id,  \rho_2,  \rho_3\}=A_3}$$
　$${\{id,  \tau_1\}}$$
　$${\{id,  \tau_2\}}$$
　$${\{id,  \tau_3\}}$$
　$${\{id\}}$$

　なお、自分自身 $${S_3}$$ や、要素が単位元だけからなる集合 $${\{id\}}$$ は『自明な部分群』となります。また、自明な部分群以外の部分群は『真部分群』となります。
　$${\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$（自明な部分群）
　$${\{id,  \rho_2,  \rho_3\}}$$（真部分群）
　$${\{id,  \tau_1\}}$$（真部分群）
　$${\{id,  \tau_2\}}$$（真部分群）
　$${\{id,  \tau_3\}}$$（真部分群）
　$${\{id\}}$$（自明な部分群）

　群の定義 (3) より、単位元があることは群の条件に必要なので、どの部分群にも単位元 $${id}$$ が含まれます。
　ここでは $${\{id,  \tau_1\}}$$ について、群の定義 (1)～(4) をすべて満たすことを確認していきます。

(1)　$${\{id,  \tau_1\}}$$ の要素の積は $${\{id,  \tau_1\}}$$ に含まれる。
　$${idid=id}$$
　$${id\tau_1=\tau_1}$$
　$${\tau_1id=\tau_1}$$
　$${\tau_1\tau_1=id}$$
より、置換の積はすべて $${\{id,  \tau_1\}}$$ に含まれます。$${\{id,  \tau_1\}}$$ は置換の積について閉じています。

(2)　結合法則は成り立つ。
例　$${(\tau_1id)\tau_1=\tau_1(id\tau_1)}$$
　任意の要素に対して成り立つので、同じ要素があっても構いません。
　結合法則は常に成り立ちます。

(3)　単位元は存在する。
　$${id\underline{id}=\underline{id}id=id}$$（変化しない）
　$${\tau_1\underline{id}=\underline{id}\tau_1=\tau_1}$$（変化しない）
より、下線部の $${id}$$ が単位元となります。

(4)　逆元は存在する。
　$${id\underline{id}=\underline{id}id=id}$$（単位元）
より、$${id}$$ の逆元は $${id}$$ です。
　$${\tau_1\underline{\tau_1}=\underline{\tau_1}\tau_1=id}$$
より、$${\tau_1}$$ の逆元は $${\tau_1}$$ です。
　下線部が各々の逆元となります。

　以上により、群の定義 (1)～(4) をすべて満たしているので、$${\{id,  \tau_1\}}$$ は部分群となります。他の部分群に対しても、同様にして群であることが証明されます。

まとめ

　ここでは『部分群』の解説をしましたが、いよいよ次は、ガロアの証明の核となる『正規部分群』の解説に入ります。部分群のうち、特別な性質をもつ『正規部分群』が、解の公式が存在するかどうかのカギを握ります。次回はそれを解説する予定していきます。

（注１）{id} が群になることの証明。

　恒等置換のみの集合 $${\{id\}}$$ が、置換の積に関して群の定義 (1)～(4) をすべて満たすことを確認していきます。
(1)　$${idid}$$ は $${\{id\}}$$ の要素である。
　$${idid=id}$$
より、$${\{id\}}$$ の要素となります。

(2)　結合法則は成り立つ。
例　$${(idid)id=id(idid)}$$
より、結合法則は成り立ちます。

(3)　単位元は存在する。
　$${id\underline{id}=\underline{id}id=id}$$（変化しない）
より、下線部の $${id}$$ が単位元となります。

(4)　逆元は存在する。
　$${id\underline{id}=\underline{id}id=id}$$（単位元）
より、$${id}$$ の逆元は下線部の $${id}$$ です。

　以上により、群の定義 (1)～(4) をすべて満たしているので、恒等置換だけからなる集合 $${\{id\}}$$ は、置換の積に関して群となります。$${id}$$ は単位元なので、$${\{id\}}$$ は単位元だけからなる群です。一般に、単位元だけからなる群は、すべての群の部分群となります。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について簡単に解説