そもそもなぜ５次以上の方程式に解の公式が存在しないのかについて、『巡回置換』との関連で解説していきます。結論的なことは、本文最後の方で述べています。

　３次方程式の解の公式の導出において、それが
　「累乗根を取ることによる、解の置換の対称性の破壊」
とつながっていることは、全章の本シリーズ (26) でやりました。そのときの（図解）を改めて再掲します。平方根、３乗根と次々と累乗根を取ることによって、式を変化させない置換（対称性）が恒等置換にまで破壊されていく過程がみて取れます。

（再掲）

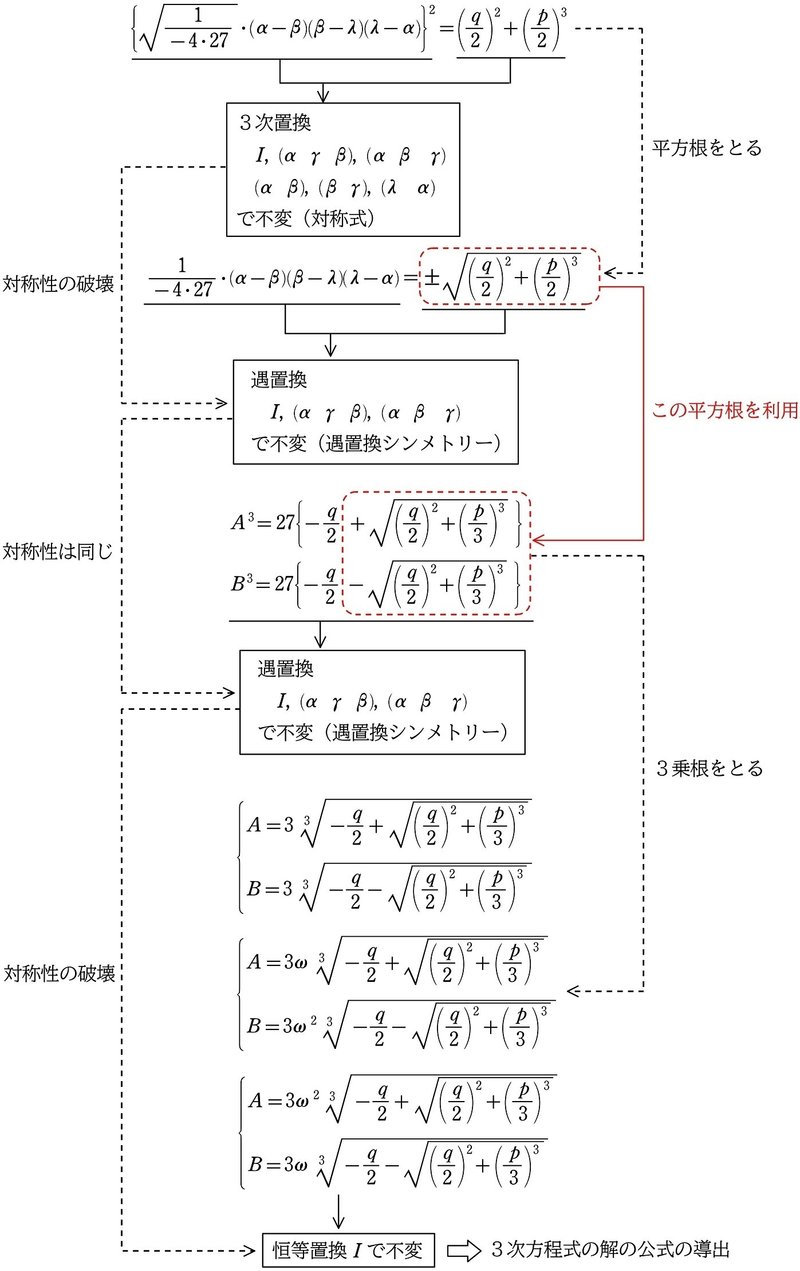
　なお、$${A,  B}$$ はラグランジュ・リゾルベントです。

$$
\begin{align*}
A&=\alpha+\omega\beta+\omega^2\gamma\\
B&=\alpha+\omega^2\beta+\omega\gamma
\end{align*}
$$

　ラグランジュ・リゾルベントの３乗 $${A^3,  B^3}$$ は差積 $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ と同じ対称性（遇置換シンメトリー）をもちます。
　（図解）の赤字部分から、$${A^3,  B^3}$$ は（差積で表せる）平方根の加減乗除で表せることからも、同じ対称性をもつことが確認できます。差積の対称性が、そのまま $${A^3,  B^3}$$ に引き継がれているのです。
　また、本シリーズで述べていませんが、４次方程式においても、解の公式の導出は上記のような「累乗根を取ることによる、解の置換の対称性の破壊」で説明されます（解説は割愛）。

（復習）３次置換の対称性の破壊

　さて、５次以上の方程式には解の公式は存在しません。解の公式が存在すれば、具体的に式変形で作り出せば証明できます。しかし存在しないことを示すためには式変形だけでは難しく、なにか別のアイデアが必要になります。
　そこで、フランスの数学者ラグランジュやガロア、ノルウエーの数学者アーベルらは、解の入れ替えの「対称性」に着目しましました。
　そのことを説明するために、改めて３次置換を復習します。ここでの３次置換とは、３次方程式の３つの解 $${\alpha,  \beta,  \gamma}$$ のすべての入れ替えのことで、次の６種類があります（本シリーズ (14)）。遇置換は３次巡回置換で、奇置換は互換で表すことができます（本シリーズ (16)）。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

　なお、互換は２つの文字の巡回置換、つまり２次巡回置換とみることもできます。例えば、互換 $${(\alpha     \beta)}$$ は、２つの文字 $${\alpha}$$ と $${\beta}$$ を
　$${\alpha \rightarrow \beta \rightarrow \alpha}$$
と巡回するよう入れ替える置換です。
　すると、３次方程式の解の公式の導出過程では、この $${➀～➅}$$ の置換が

$$
\begin{align*}
➀、➁、➂&、➃、➄、➅（３次置換）\\
&\downarrow  {\small 平方根を取る}\\
➀、&➁、➂（遇置換）\\
&\downarrow    {\small ３乗根を取る}\\
&➀（恒等置換）
\end{align*}
$$

と次々と絞られていく（破壊されていく）過程がみて取れます。これは平方根、３乗根と、次々と累乗根を取っていく過程と対応しています。そして最後、恒等置換のみになったときに初めて、解の公式が実現可能となります（本シリーズ (20)）。
　そこで対称性の破壊という観点で、もう一度３次方程式の解の公式の導出過程をみていきましょう。後で詳しく述べますが『巡回置換』という考え方がキーワードになってきます。

３次方程式の解の公式が存在する理由

　ここで、本シリーズでやってきた３次方程式の解の公式の導出方法を改めて眺めると、次のステップを辿っています。ここからのキーワードは『２次巡回置換』と『３次巡回置換』です。
　なお、「対称式」とは文字をどのように入れ替えても変化しない式のこと、「解の式」とは３次方程式の解 $${\alpha,  \beta,  \gamma}$$ で表される式のことです。
　なお、以下の (step1) は、主に本シリーズ (12) の内容をまとめています。主に「条件Ⅰ」の部分です。「２次巡回置換」の「２」という数がキーワードになります。

(step1)
　３次方程式の解を $${\alpha,  \beta,  \gamma}$$ とし、その３つの解の３次置換を考える
$${\longrightarrow}$$ ３次置換はすべて互換（および互換の積）で表せる（本シリーズ (15)）

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta)(\alpha     \beta)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma)(\alpha     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta)(\alpha     \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

$${\longrightarrow}$$ 互換は「２次巡回置換」とみなすこともできる
$${\longrightarrow}$$ 互換は同じものを２回連続作用させると元に戻る
$${\longrightarrow}$$ そこで「２乗した $${X^2}$$ は対称式（つまり２次巡回置換で変化しない）でありながらも、その平方根である $${X}$$ では対称性が破壊される（つまり２次巡回置換で変化する）」ような解の式 $${X}$$ を考える
$${\longrightarrow}$$ そのような解の式 $${X}$$ として、差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を取ることができる
$${\longrightarrow}$$ 差積の２乗
　$${{(X_3)}^2={\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}}^2}$$
は対称式なので、３次方程式の係数の加減乗除で計算できる
$${\longrightarrow}$$ 一方、その平方根（２乗恨）である差積そのもの
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
は対称式ではなく、奇置換で $${-1}$$ 倍に変化する
$${\longrightarrow}$$ 差積を変化させないのは遇置換のみ
$${\longrightarrow}$$ 差積を用いること（平方根を取るという操作）によって、解の置換の対称性を遇置換シンメトリーまで破壊することに成功

＊＊＊

　ここまでが最初のステップです。上の（図説）でいうと、平方根を取る計算過程です。　
　$${X^2=C（対称式）}$$
という２次方程式を、平方根を用いて
　$${X=\pm\sqrt{C}}$$
と解くことに対応しています。
　(step1) で、完全な対称性をもつ対称式の対称性（３次置換で不変）を、遇置換シンメトリーにまで破壊できました。
　そして次の (step2) に入ります。遇置換シンメトリーからスタートします。
　なお、(step2) は主に本シリーズ (13)、(14) の内容をまとめています（注１）。主に「条件Ⅱ」の部分です。「３次巡回置換」の「３」という数がキーワードになります。

(step2)
　遇置換はすべて３次巡回置換（および３次巡回置換の積）で表せる（本シリーズ (16)）。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換
\end{align*}
$$

$${\longrightarrow}$$ 逆に３次巡回置換はすべて遇置換（偶数個の互換で表せる）である
　$${(\alpha     \gamma     \beta)=(\alpha     \gamma)(\alpha     \beta)}$$
　$${(\alpha     \beta     \gamma)=(\alpha     \beta)(\alpha     \gamma)}$$
$${\longrightarrow}$$ ３次巡回置換は同じものを３回連続作用させると元に戻る
$${\longrightarrow}$$ そこで「３乗した $${Y^3}$$ は遇置換シンメトリーをもつ（つまり３次巡回置換で変化しない）が、その３乗根である $${Y}$$ では遇置換シンメトリーが破壊される（つまり３次巡回置換で変化する）」ような解の式 $${Y}$$ を考える
$${\longrightarrow}$$ そのような $${Y}$$ として、ラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
を取ることができる。
$${\longrightarrow}$$ ラグランジュ・リゾルベントの３乗
　$${A^3={(\alpha+\omega\beta+\omega^2\gamma)}^3}$$
は遇置換（３次巡回置換）では変化しない（遇置換シンメトリーをもつ）
$${\longrightarrow}$$ 一方、ラグランジュ・リゾルベントそのもの
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
は遇置換シンメトリーをもたず、恒等置換以外の遇置換（３次巡回置換）で $${\omega}$$ または $${\omega^2}$$ 倍に変化する（注２）
$${\longrightarrow}$$ ラグランジュ・リゾルベントを変化せない置換は恒等置換のみ
$${\longrightarrow}$$ ラグランジュ・リゾルベントを用いること（３乗根を取るという操作）によって、解の置換の対称性を恒等置換まで破壊することに成功
$${\longrightarrow}$$ ３次方程式の解の公式の導出が可能となる

＊＊＊

　これで３次方程式の解の公式が得られることになります。上の（図説）でいうと、３乗根を取る計算過程です。
　$${X^3=D（遇置換シンメトリーをもつ式）}$$
という３次方程式を、３乗根を用いて
　$${X=\sqrt[3]{D},  \omega\sqrt[3]{D},  \omega^2\sqrt[3]{D}}$$
と解くことに対応しています。
　(step2) で、対称性を恒等置換にまで破壊できたことによって、解の公式の導出が可能となりました。
　なお、$${Y}$$ を変化させる３次巡回置換は
　$${(\alpha     \gamma     \beta)}$$ と $${(\alpha     \beta     \gamma)}$$
です。 下の遇置換のうち $${➁}$$ と $${➂}$$ です。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換
\end{align*}
$$

３次巡回置換 $${(\alpha     \gamma     \beta)}$$ と $${(\alpha     \beta     \gamma)}$$ で、$${Y}$$（つまりラグランジュ・リゾルベント $${A}$$）は変化します（本シリーズ (6)）（注２）。

　すると、５次方程式の場合はどうでしょうか。もし解の公式が存在するなら、上記の (step1) ～ (step2) のように、次々と累乗根を取ることによって、恒等置換まで対称性を破壊していくことが可能です。

（大幅修正）対称性の破壊は『巡回置換』が鍵を握ること

　さて、ここからやや抽象的な話になっていきますが、冒頭の方で、キーワードは『２次巡回置換』と『３次巡回置換』といいました。対称性の破壊には『巡回置換』が鍵を握ります。
　なお、２次巡回置換とは互換のことです。

　さて、(step1) では

$$
\begin{align*}
&３次置換はすべて\bm{２}次巡回置換（互換）で表せる\\
&\downarrow\\
&\bm{２}次巡回置換は\bm{２}回連続作用すれば元に戻る\\
&\downarrow\\
&X^2（X  の\bm{２}乗）は対称式\\
&\downarrow\\
&X^2  の\bm{２}乗恨（平方根）を取って、\\
&対称性を遇置換シンメトリーにまで破壊
\end{align*}
$$

という「２」との関連が見られます。このような対称性の破壊を実現させる解の式 $${X}$$（$${X^2}$$ の平方根）として、３つの解の差積

$$
\begin{align*}
X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\end{align*}
$$

がありました。

　(step2) では

$$
\begin{align*}
&遇置換はすべて\bm{３}次巡回置換で表せる\\
&\downarrow\\
&\bm{３}次巡回置換はすべて遇置換である\\
&\downarrow\\
&３次巡回置換は\bm{３}回連続作用すれば元に戻る\\
&\downarrow\\
&Y^3（Y  の\bm{３}乗）は遇置換シンメトリーをもつ\\
&\downarrow\\
&Y^3  の\bm{３}乗恨を取って対称性を恒等置換に破壊
\end{align*}
$$

という「３」との関連が見られます。このような対称性の破壊を実現させる解の式 $${Y}$$（$${Y^3}$$ の３乗根）として、ラグランジュ・リゾルベント

$$
\begin{align*}
A&=\alpha+\omega\beta+\omega^2\gamma
\end{align*}
$$

がありました。この様に、累乗根（平方根や３乗根）を取ることと「巡回置換」は関連があります。「巡回置換」だけに目を向けると、３次方程式の解の公式の導出は次のようにまとめられます。

$$
\begin{gather*}
対称式（\underset{互換}{２次巡回置換}で不変）\\
\hspace{-8pt}{\small 差積  X_2  の添加}  \downarrow  {\small 対称性の破壊}\\
\underset{遇置換シンメトリーをもつ}{平方根のある式体系}（３次巡回置換で不変）\\
\hspace{17pt}{\small A  の添加}  \downarrow  {\small 対称性の破壊}\\
３乗根のある式体系（恒等置換で不変）\\
\downarrow\\
３次方程式の解の公式が導出
\end{gather*}
$$

　すると、５次方程式においても、例えば一例として

$$
\begin{gather*}
対称式（\underset{互換}{２次巡回置換}で不変）\\
\hspace{8pt}{\small 差積の添加} \downarrow  {\small 対称性の破壊}\\
\underset{遇置換シンメトリーをもつ}{平方根のある式体系}（３次巡回置換で不変）\\
\hspace{17pt}{\small ？の添加} \downarrow  {\small 対称性の破壊}\\
３乗根のある式体系（５次巡回置換で不変）\\
\hspace{17pt}{\small ？の添加}  \downarrow  {\small 対称性の破壊}\\
５乗根のある式体系（恒等置換で不変）\\
\downarrow\\
５次方程式の解の公式が導出？
\end{gather*}
$$

のように、「？」のところで何かラグランジュ・リゾルベントのような都合のよい式が存在し、次々と対称性を破壊していけば、５次方程式の解の公式が実現できそうな気もします。
　なお、何次方程式であっても解の差積は作ることができるので、最初に差積を添加して対称性を破壊することは、解の公式を構成する上での常套手段となります（本シリーズ (14)、(21)）。
　また４次巡回置換は４乗根を取ることと関連はしていますが、４乗根は
　$${\sqrt[4]{3}=\sqrt[2]{\sqrt[2]{3}}=\sqrt{\sqrt{3}}}$$（平方根の $${2}$$ は省略する）
のように「平方根の平方根」によって表現できるので、先に平方根の添加があれば、４乗根のある式体系はすでに存在しています。
　しかし、５次以上の方程式には解の公式は存在しません。５次以上の方程式の場合、３次巡回置換で不変な式体系、つまり遇置換シンメトリーまで対称性を破壊できますが、さらに対称性を破壊できないことが証明されます。

$$
\begin{gather*}
対称式（\underset{互換}{２次巡回置換}で不変）\\
\hspace{8pt}{\small 差積の添加} \downarrow  {\small 対称性の破壊}\\
\underset{遇置換シンメトリーをもつ}{平方根のある式体系}（３次巡回置換で不変）\\
\hspace{60pt}{\small ？の添加} \downarrow  \Leftarrow {\small ここがつながらない}\\
？乗根のある式体系
\end{gather*}
$$

　以下、それについて本文より簡潔にした形でみていきます。詳しい証明は本編の方でやっているので、そちらの方もご覧ください（本シリーズ (14) ～ (17)）。

５次方程式に解の公式が存在しない理由

　証明は背理法でおこないます（注３）。
　「５次方程式に解の公式が存在する」と仮定します（背理法の仮定）。詳しく言うと、５次方程式の解の公式を、加減乗除 ($${\small +,  -,  \times,  \div}$$) と累乗根 ($${\scriptsize \sqrt{　},  \sqrt[3]{　},  \cdots}$$) を用いて構成できると仮定します。そして矛盾を導き出すことによって、最初に立てた仮定「５次方程式に解の公式が存在する」ことが間違っていることが分かり、５次方程式に解の公式が存在しないと結論されます。
　まず５次方程式においても (step1) はクリアーできます。３次方程式と同様、「２次巡回置換」が鍵を握り、「２」という数がキーワードになってきます。主に本シリーズ (14) の「条件Ⅰ」の内容です。具体的にみていきますと

(step1)
　５次方程式の解を $${x_1,  x_2,  x_3,  x_4,  x_5}$$ とし、その５つの解の置換を考える。その置換のことを５次置換という
$${\longrightarrow}$$ ５次置換はすべて互換で表せる（本シリーズ (15)）
$${\longrightarrow}$$ 互換は２次巡回置換とみなすこともできる
$${\longrightarrow}$$ 互換は同じものを２回連続作用させると元に戻る
$${\longrightarrow}$$ そこで「２乗した $${X^2}$$ は対称式でありながらも、その平方根である $${X}$$ では対称性が破壊される」ような解の式 $${X}$$ を考える
$${\longrightarrow}$$ そのような解の式 $${X}$$ として、差積

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&\
\end{align*}
$$

を考えることができる
$${\longrightarrow}$$ 差積の２乗 $${{(X_5)}^2}$$ は対称式なので、５次方程式の係数の加減乗除で計算できる
$${\longrightarrow}$$ 一方、その平方根（２乗恨）である差積そのものは対称式ではなく、奇置換（奇数個の互換の積）で $${-1}$$ 倍に変化する（本シリーズ (14)）
$${\longrightarrow}$$ 差積を変化させないのは遇置換（偶数個の互換の積）のみ
$${\longrightarrow}$$ 差積を用いること（平方根を取るという操作）によって、解の置換の対称性を遇置換シンメトリーまで破壊することに成功

＊＊＊

　このようにして、５次方程式について、完全な対称性をもつ対称式の対称性（５次置換で不変）を、遇置換シンメトリーまで破壊できました。
　しかし、次の (step2) が問題です。５次方程式においては、遇置換シンメトリーをさらに破壊していくことができません。以下そのことをみていきます。３次方程式と同様、「３次巡回置換」が鍵を握り、「３」という数がキーワードになってきます。主に本シリーズ (16) の「条件Ⅱ」の内容です。

(step2)
　５次置換のうち、遇置換はすべて３次巡回置換で表せる（本シリーズ (16)）
（例）$${(x_1     x_2)(x_1     x_3)=(x_1     x_2     x_3)}$$
$${\hspace{30pt}(x_1     x_2)(x_3     x_4)=(x_1     x_3     x_2)(x_3     x_4     x_3)}$$
$${\longrightarrow}$$ ３次巡回置換はすべて遇置換である
（例）$${(x_1     x_2     x_3)=(x_1     x_2)(x_1     x_3)}$$
$${\longrightarrow}$$ ３次巡回置換は同じものを３回連続作用させると元に戻る
$${\longrightarrow}$$ そこで「３乗した $${Y^3}$$ は遇置換シンメトリーをもつ（３次巡回置換で変化しない）が、その３乗根である $${Y}$$ では遇置換シンメトリーが破壊される（ある３次巡回置換で変化する）」ような解の式 $${Y}$$ を考える

＊＊＊

　３次方程式では、解の式 $${Y}$$ はラグランジュ・リゾルベントでした。５次方程式においても、このような $${Y}$$ が存在すれば、遇置換シンメトリーをさらに破壊していくことが可能となります。しかし、５次方程式では $${Y}$$ は存在しないことが証明されます。それは、次の式が存在するためです。

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

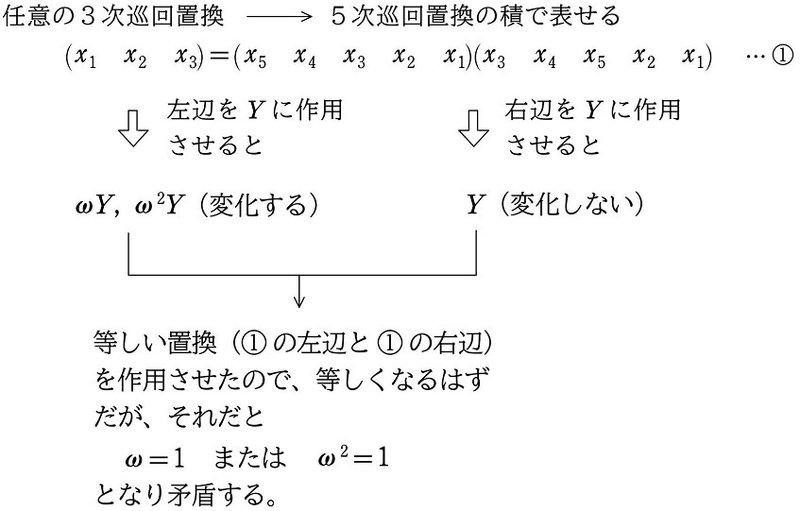
　これは、「任意の３次巡回置換は５次巡回置換の積」で表すことができるという公式です。この式は本シリーズ (17) で（小学５年生の森田君が）証明しています。なぜこの公式が、５次方程式の解の公式の存在を否定するのでしょうか？
　ここからは、その証明をもう一度みていきます。詳しくは本シリーズ (17) を参照ください。

　先ほど (step2) で

「３乗した $${Y^3}$$ は遇置換シンメトリーをもつ（３次巡回置換で変化しない）が、その３乗根である $${Y}$$ では遇置換シンメトリーが破壊される（ある３次巡回置換で変化する）」ような解の式 $${Y}$$ を考える

と書きました。なお、$${Y}$$ を変化させるのは、必ずしもすべての３次巡回置換ではなく、少なくとも１つあればよいことを注意しておきます。「ある３次巡回置換で変化する」と「ある」という言葉を付けているのはそういう理由です。少なくとも１つあれば、遇置換シンメトリーを破壊することができます。
　その $${Y}$$ を変化させる「ある３次巡回置換」を $${(x_1     x_2     x_3)}$$ とすると、$${Y^3}$$ は遇置換シンメトリーをもつので、$${Y^3}$$ に $${(x_1     x_2     x_3)}$$ を作用させても変化しません（遇置換は必ず３次巡回置換で表せる）。よって

$$
\begin{align*}
(x_1     x_2     x_3)Y^3=Y^3　\cdots ➁
\end{align*}
$$

　なお、５次方程式の解 $${x_1,  x_2,  x_3,  x_4,  x_5}$$ はそれぞれ対等で区別が無いので、 代表で選んだ $${(x_1     x_2     x_3)}$$ は、一般性を失わず任意の３次巡回置換とみなすことができます。
　ここで、$${(x_1     x_2     x_3)}$$ は $${Y^3}$$ の $${Y}$$ に作用し、３乗は変えないので

$$
\begin{align*}
(x_1     x_2     x_3)Y^3=\{(x_1     x_2     x_3)Y\}^3　\cdots ➂
\end{align*}
$$

$${➂=➁}$$ より

$$
\begin{align*}
\{(x_1     x_2     x_3)Y\}^3=Y^3
\end{align*}
$$

ここで $${\omega}$$ の性質（本シリーズ (24)）
　$${\omega^3=1}$$
　$${{(\omega^2)}^3=\omega^6={(\underset{1}{\underline{\omega^3}})}^2=1^3=1}$$
に注意すると、これを満たす $${(x_1     x_2     x_3)Y}$$ は

$$
\begin{align*}
(x_1     x_2     x_3)Y=Y,   \omega Y,   \omega^2Y
\end{align*}
$$

の３通りがありえます。これは $${x^3=8(=2^3)}$$ の解は
　$${x=2,   2\omega,   2\omega}$$
となるのと同じ計算形式です（本シリーズ (2)）。

　しかし、$${Y}$$ はその「ある３次巡回置換」 $${(x_1     x_2     x_3)}$$ で変化しなければならないので、$${(x_1     x_2     x_3)Y=Y}$$ は却下されて

$$
\begin{align*}
(x_1     x_2     x_3)Y=\omega Y,   \omega^2Y　\cdots ➃
\end{align*}
$$

の２通りに絞られます。

　ここで、任意の５次巡回置換を考えます。任意の５次巡回置換は、必ず偶数個の互換の積で表せるので遇置換です（本シリーズ (15)）。
（例）

$$
\begin{align*}
\underset{\footnotesize ５次巡回置換}{\underline{(x_1     x_2     x_3     x_4     x_5)}}=\underset{\footnotesize 偶数個（４個）の互換の積}{\underline{(x_1     x_2)(x_1     x_3)(x_1     x_4)(x_1     x_5)}}
\end{align*}
$$

すると、$${Y^3}$$ は遇置換シンメトリーをもつので、遇置換で任意の５次巡回置換を作用させても変化しません。

$$
\begin{align*}
Y^3 \xrightarrow[\overset{\raisebox{5pt}{\small ↑}}{任意の５次巡回置換}]{} Y^3 {\small（変化しない）}
\end{align*}
$$

　そこで、５次方程式の解 $${x_1,  x_2,  x_3,  x_4,  x_5}$$ を用いて得られる任意の５次巡回置換を

$$
\begin{align*}
(l     m     n     o     p)
\end{align*}
$$

とおきます。つまり、$${l,  m,  n,  o,  p}$$ は $${x_1,  x_2,  x_3,  x_4,  x_5}$$ のどれかです。
　この５次巡回置換を $${Y^3}$$ に作用させることは、数式で
　$${(l     m     n     o     p)Y^3}$$
と表記しますが、$${Y^3}$$ は任意の５次巡回置換で変化しないことから

$$
\begin{align*}
(l     m     n     o     p)Y^3=Y^3　\cdots ➄
\end{align*}
$$

さらに、置換は $${Y}$$ に作用して指数部分 $${3}$$ は変化させないので

$$
\begin{align*}
(l     m     n     o     p)Y^3=\{(l     m     n     o     p)Y\}^3　\cdots ➅
\end{align*}
$$

すると $${➅=➄}$$ より

$$
\begin{align*}
\{(l     m     n     o     p)Y\}^3=Y^3
\end{align*}
$$

ここで、先ほどやったように $${\omega}$$ の性質（本シリーズ (24)）
　$${\omega^3=1}$$
　$${{(\omega^2)}^3=\omega^6={(\underset{1}{\underline{\omega^3}})}^2=1^3=1}$$
に注意すると、これを満たす $${(l     m     n     o     p)Y}$$ は

$$
\begin{align*}
(l     m     n     o     p)Y=Y,  \omega Y,  \omega^2Y　\cdots ➆
\end{align*}
$$

の３通りがありえます（本シリーズ (17)）。
　ここで、$${(l     m     n     o     p)Y}$$ の行き先が、$${Y,  \omega Y,  \omega^2Y}$$ のどれになるかを決定します。
　そのためには、５次巡回置換は同じものを５回連続作用させると、変化しないで元に戻るという性質を利用します。５次巡回置換 $${(l     m     n     o     p)}$$ を５回連続作用させることを
　$${(l     m     n     o     p)^5}$$
と表記すると、それを解の式 $${Y}$$ に作用させても変化しないので

$$
\begin{align*}
(l     m     n     o     p)^5Y=Y　\cdots ➇
\end{align*}
$$

　ここで、$${➆}$$ において
(case1)　$${(l     m     n     o     p)Y=Y}$$ のとき
(case2)　$${(l     m     n     o     p)Y=\omega Y}$$ のとき
(case3)　$${(l     m     n     o     p)Y=\omega^2Y}$$ のとき
と場合分けをして、ひとつひとつ確認していきます。先ほどの $${➇}$$ を満たすかどうかを確認します。

(case1)　$${(l     m     n     o     p)Y=Y}$$ のとき
　これは、$${(l     m     n     o     p)}$$ を１回作用させても $${Y}$$ は変化しないという式です。このとき、この５次巡回置換 $${(l     m     n     o     p)}$$ を $${Y}$$ に５回連続作用させると

$$
\begin{align*}
&  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（１回目）}\\
{\small 変化しない \rightarrow}  &  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（２回目）}\\
{\small 変化しない \rightarrow}  &  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（３回目）}\\
{\small 変化しない \rightarrow}  &  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（４回目）}\\
{\small 変化しない \rightarrow}  &  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（５回目）}\\
{\small 変化しない \rightarrow}  &  Y
\end{align*}
$$

より

$$
\begin{align*}
&  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)^5  を作用}　　　　\\
{\small 変化しない \rightarrow}  &  Y
\end{align*}
$$

よって

$$
\begin{align*}
(l     m     n     o     p)^5Y=Y
\end{align*}
$$

これは、$${➇}$$ 式

$$
\begin{align*}
(l     m     n     o     p)^5Y=Y　\cdots ➇
\end{align*}
$$

を満たします。よって、(case1)
　$${(l     m     n     o     p)Y=Y}$$
は正しい結果となります。

(case2)　$${(l     m     n     o     p)Y=\omega Y}$$ のとき
　これは、$${(l     m     n     o     p)}$$ を１回作用させると、$${Y}$$ は $${\omega}$$ 倍に変化するという式です。このとき、この５次巡回置換 $${(l     m     n     o     p)}$$ を $${Y}$$ に５回連続作用させると

$$
\begin{align*}
&  Y\\
{\small \omega  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（１回目）}\\
&\omega Y\\
{\small \omega  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（２回目）}\\
&\omega^2Y\\
{\small \omega  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（３回目）}\\
&\omega^3Y\\
{\small \omega  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（４回目）}\\
&\omega^4Y\\
{\small \omega  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（５回目）}\\
&\omega^5Y
\end{align*}
$$

より

$$
\begin{align*}
&  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)^5  を作用}　　\\
&\omega^5Y
\end{align*}
$$

よって

$$
\begin{align*}
(l     m     n     o     p)^5Y=\omega^5Y
\end{align*}
$$

$${\omega^5=\underset{1}{\underline{\omega^3}}\cdot\omega^2=\omega^2}$$ より

$$
\begin{align*}
(l     m     n     o     p)^5Y=\omega^2Y
\end{align*}
$$

しかし、これは満たしていないことが分かります。$${\omega}$$ は「３乗して１になる数（１の３乗根）のうち複素数である定数」、具体的には
　$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$　または　$${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので（本シリーズ (24)）、$${➇}$$ 式

$$
\begin{align*}
(l     m     n     o     p)^5Y=Y　\cdots ➇
\end{align*}
$$

を満たしません。よって、(case2)
　$${(l     m     n     o     p)Y=\omega Y}$$
は不適となります。

(case3)　$${(l     m     n     o     p)Y=\omega^2Y}$$ のとき
　これは、$${(l     m     n     o     p)}$$ を１回作用させると、$${Y}$$ は $${\omega^2}$$ 倍に変化するという式です。このとき、この５次巡回置換 $${(l     m     n     o     p)}$$ を $${Y}$$ に５回連続作用させると

$$
\begin{align*}
&  Y\\
{\small \omega^2  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（１回目）}\\
&\omega^2Y\\
{\small \omega^2  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（２回目）}\\
&\omega^4Y\\
{\small \omega^2  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（３回目）}\\
&\omega^6Y\\
{\small \omega^2  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（４回目）}\\
&\omega^8Y\\
{\small \omega^2  倍}  &\Downarrow  {\small \leftarrow (l     m     n     o     p)  を作用（５回目）}\\
&\omega^{10}Y
\end{align*}
$$

より

$$
\begin{align*}
&  Y\\
&\Downarrow  {\small \leftarrow (l     m     n     o     p)^5  を作用}　　\\
&\omega^{10}Y
\end{align*}
$$

よって

$$
\begin{align*}
(l     m     n     o     p)^5Y=\omega^{10}Y
\end{align*}
$$

$${\omega^{10}=\omega^3\cdot\omega^3\cdot\omega^3\cdot\omega={(\underset{1}{\underline{\omega^3}})}^3\cdot\omega=1^3\cdot\omega=\omega}$$ より

$$
\begin{align*}
(l     m     n     o     p)^5Y=\omega Y
\end{align*}
$$

しかし、これも満たしていないことが分かります。先に述べたように $${\omega}$$ は
　$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$　または　$${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので、$${➇}$$ 式

$$
\begin{align*}
(l     m     n     o     p)^5Y=Y　\cdots ➇
\end{align*}
$$

を満たしません。よって、(case3)
　$${(l     m     n     o     p)Y=\omega^2 Y}$$
は不適となります。
　以上より、(case1) のときのみが成り立ち、$${(l     m     n     o     p)Y}$$ の行き先は

$$
\begin{align*}
(l     m     n     o     p)Y=Y　\cdots ➈
\end{align*}
$$

とただ１通りに決まります。$${Y}$$ そのものは、任意の５次巡回置換で変化しないことが分かりました。
　ここで最初に示した $${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

が登場します。
　まず、$${➀}$$ の左辺 $${(x_1     x_2     x_3)}$$ は、解の式 $${Y}$$ に作用させると変化させる３次巡回置換です。$${Y}$$ にこの３次巡回置換 $${(x_1     x_2     x_3)}$$ を作用させると、$${➃}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)Y=\omega Y,  \omega^2Y　\cdots ➃
\end{align*}
$$　

となることはすでにやりました。
　次に $${➀}$$ の右辺を見てみます。これは５次巡回置換の積です。先ほど $${➈}$$ 式

$$
\begin{align*}
(l     m     n     o     p)Y=Y　\cdots ➈
\end{align*}
$$

を証明しました。これは、解の式 $${Y}$$ に任意の５次巡回置換 $${(l     m     n     o     p)}$$ を作用させても変化しないという式です。
　$${(l     m     n     o     p)}$$ は任意の５次巡回置換なので、どのような５次巡回置換を持ってきても $${➈}$$ は成り立ちます。つまり、$${➀}$$ の右辺に表れる２つの５次巡回置換を持ってきても $${➈}$$ は成り立つので

$$
\begin{align*}
(x_5     x_4     x_3     x_2     x_1)Y&=Y　\cdots ➉\\
(x_3     x_4     x_5     x_2     x_1)Y&=Y　\cdots ⑪
\end{align*}
$$

ここで、$${Y}$$ に $${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

の左辺である
　$${(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)}$$
を作用させてみましょう。本シリーズでは置換の積を左から（前から）順に作用させると定義しているので

$$
\begin{align*}
&  Y\\
&\Downarrow  {\small \leftarrow (x_5     x_4     x_3     x_2     x_1)  を作用}\\
{\small ➉ より変化しない \rightarrow}  &  Y\\
&\Downarrow  {\small \leftarrow (x_3     x_4     x_5     x_2     x_1)  を作用}\\
{\small ⑪ より変化しない \rightarrow}  &  Y
\end{align*}
$$

より、$${Y}$$ は変化しないので

$$
\begin{align*}
(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)Y=Y　\cdots ⑫ \end{align*}
$$

ここで $${➃}$$ と $${⑫}$$ を並べてみます。

$$
\begin{align*}
(x_1     x_2     x_3)Y&=\omega Y,  \omega^2Y　\cdots ➃\\
(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)Y&=Y\hspace{32pt}　\cdots ⑫
\end{align*}
$$

すると、おかしいことに気付きます。改めて $${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

を確認すると、等しい置換を $${Y}$$ に作用させても等しくなるので

$$
\begin{align*}
(x_1     x_2     x_3)Y=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)Y
\end{align*}
$$

すると、左辺は $${➃}$$ 、右辺は $${⑫}$$ より、$${➃}$$ と $${⑫}$$ は等しくならないといけません。すると、$${➃}$$ は $${\omega Y}$$ または $${\omega^2Y}$$ の２通りがあるので

$$
\begin{align*}
\underset{➃ より \omega Y,   \omega^2Y}{\underline{(x_1     x_2     x_3)Y}}=\underset{⑫ より Y}{\underline{(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)Y}}
\end{align*}
$$

$${➃=⑫}$$ より

$$
\begin{align*}
\omega Y=Y　または　\omega^2Y=Y
\end{align*}
$$

すると、$${Y\ne0}$$ なので

$$
\begin{align*}
\omega=1　または　\omega^2=1
\end{align*}
$$

となり矛盾します。$${\omega}$$ は
　$${\omega=\dfrac{-1+\sqrt{2}i}{2}}$$　または　$${\dfrac{-1-\sqrt{2}i}{2}}$$
という定数なので、これは矛盾です。

　すると、矛盾が生じた理由は「５次方方程式に解の公式が存在する」と仮定したこと、詳しく言うと、５次方程式の解の公式を加減乗除 ($${\small +,  -,  \times,  \div}$$) と累乗根 ($${\scriptsize \sqrt{　},  \sqrt[3]{　},  \cdots}$$) を用いて構成できると仮定したことにあります。つまり、この仮定が間違いであることが示されたので、背理法により５次方程式に解の公式が存在しないことが証明されました。

　なお、２次方程式、３次方程式、４次方程式については、この議論は適用できません。本証明では、次の $${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

が重要な役割を担いましたが、２次方程式は２つの解、３次方程式は３つの解、４次方程式は４つの解までしか持たないので、５次方程式の５つの解
　$${x_1,  x_2,  x_3,  x_4,  x_5}$$
で構成される $${➀}$$ 式は、４次以下の方程式では構成できません。実際、４次方程式までには解の公式は存在します。

　また６次方程式の場合は、６次方程式には６つの解
　$${x_1,  x_2,  x_3,  x_4,  x_5,  x_6}$$
があるので、その６つの解から任意に３つを選んで３次巡回置換を作ることができ、その３次巡回置換は５次巡回置換の積で表すことができるので、５次方程式のときと同様にして、$${➀}$$ を用いて解の公式が存在しないことが証明されます。つまり６次方程式においても、構成可能な式の拡大は差積の添加（平方根の添加）までで、それ以上は拡大できない（つまり、対称性の破壊は遇置換シンメトリーまでで、それ以上破壊できない）ということになります。
　これは７次方程式、８次方程式 $${\cdots}$$ と次数が高くなっても同じことが言えるので、これによって、５次以上の方程式には解の公式が存在しないことが証明されました。

（まとめ）証明の流れをザックリと

　５次以上の方程式に解の公式が存在しないことについて、$${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

が決定的な役割を果たすことはすでに解説しました。
　右辺は３次巡回置換、左辺は５次巡回置換（の積）です。３次巡回置換も５次巡回置換もどちらも遇置換なので、遇置換シンメトリーをもつ解の式 $${Y^3}$$ に作用させても変化しません。
　そこで、$${➀}$$ を用いた証明の流れを再び確認していきます。遇置換シンメトリーまで破壊されたところからスタートします。本記事 (step2) のまとめです。
　まず、$${➀}$$ の左辺については

$$
\begin{gather*}
５次置換のうち遇置換を考える（遇置換シンメトリー）\\
\downarrow\\
任意の遇置換は３次巡回置換で表せる\\
\downarrow\\
逆に任意の３次巡回置換は遇置換である\\
\downarrow\\
ここで、ある３次巡回置換  (x_1     x_2     x_3)  を考える\\
\downarrow\\
Y^3  は遇置換シンメトリーをもつという条件より\\
\downarrow\\
Y^3  に  (x_1     x_2     x_3)  を作用させても変化しない\\
\downarrow\\
このことにより\\
\downarrow\\
Y  に  (x_1     x_2     x_3)  を作用させると\\
\downarrow\\
Y  は  Y,  \omega Y,  \omega^2Y  の３通りの変化の可能性があるが\\
\downarrow\\
Y  は遇置換シンメトリーが破壊されている\\
\hspace{18pt}（ある３次巡回置換で変化する）という条件より\\
\downarrow\\
Y  に  \underset{①  の左辺}{\underline{(x_1     x_2     x_3)}}  を作用させると  \omega Y,  \omega^2Y  に変化する\\
\downarrow\\
つまり、(x_1     x_2     x_3)Y=\omega Y,  \omega^2Y　\cdots (*1)
\end{gather*}
$$

＊＊＊

　ここだけみると、３次方程式のときと同様、遇置換シンメトリーが破壊されたように思えます。

　一方、$${➁}$$ の右辺については

$$
\begin{gather*}
５次巡回置換はすべて遇置換である\\
\downarrow\\
Y^3  は遇置換シンメトリーをもつという条件より\\
\downarrow\\
Y^3  に任意の５次巡回置換を作用させても変化しない\\
\downarrow\\
このことにより\\
\downarrow\\
Y  に任意の５次巡回置換を作用させると\\
\downarrow\\
Y  は  Y,  \omega Y,  \omega^2Y  の３通りの変化の可能性があるが\\
\downarrow\\
５次巡回置換は５回作用させると変化しないことから\\
\downarrow\\
Y  に任意の５次巡回置換を作用させても変化しないことが結論される\\
\downarrow\\
その結果\\
\downarrow\\
Y  に  \underset{① の右辺}{\underline{(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)}}\\
\hspace{24pt}を作用させても、Y  のままで変化しない　\cdots (*2)\\
\downarrow\\
つまり、(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)Y=Y　\cdots (*2)
\end{gather*}
$$

＊＊＊

すると、$${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

より、$${(*1)}$$ と $${(*2)}$$ は等しくならなければいけませんが、等しくないので矛盾します。
　$${➀}$$ の左辺を $${Y}$$ に作用させると $${\omega Y,  \omega^2Y}$$、$${➀}$$ の右辺を $${Y}$$ に作用させると $${Y}$$ となりますが、$${\omega\ne 1}$$ より $${(*1)}$$ と $${(*2)}$$ は等しくなりません。
　この矛盾により、５次以上の方程式には解の公式が存在しないことが証明されます。

結局、なぜ５次方程式に解の公式が存在しないのか

　なかなか言語化するのは難しいですが、３次巡回置換は遇置換です。よって３乗根を取ることで、遇置換シンメトリーを破壊できることが期待できます。
　しかし５次方程式においては、$${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

により、３巡回置換を同じく遇置換である５次巡回置換（の積）で表されてしまうため、遇置換シンメトリーをもちつつもその破壊を誘導してくれる解の式（証明では $${Y^3}$$）をうまく導入しようとしても、遇置換シンメトリーを破壊することができないことになります。
　遇置換シンメトリーをさらに破壊できない、つまり恒等置換にまで破壊できないことをもって、本シリーズでは５次方程式には解の公式が存在しないとの結論に至りました（本シリーズ (20)）。
　また、$${➀}$$ を構成するためには５次巡回置換、つまり５つの解が必要です。よって解の公式が存在しないのは５次以上の方程式だと結論されます。

　うまく言えているのか分かりませんが、この辺の言語化は非常に難しいので、良い表現方法がないかもう一度考えてみます。

終わりに

　アーベルの証明も、この $${➀}$$ 式

$$
\begin{align*}
(x_1     x_2     x_3)=(x_5     x_4     x_3     x_2     x_1)(x_3     x_4     x_5     x_2     x_1)　\cdots ➀
\end{align*}
$$

を用いた証明になっていますが、かなり技巧的な式変形を行っていて、今の視点でみれば分かりにくいものになっていると思います。その当時はまだ、集合などの数学的概念が無かったからかもしれません。

　そこで、本シリーズでは以下の参考文献

『代数学概論』高木貞治著
『不可能の証明』津田文夫著
　内容はアーベルの証明を、現代的な視点を加味して簡潔に書いたもののようです。
　アーベルの原論文は以下を参考。
『群と代数方程式』守屋美賀雄訳・解説
『アーベルの証明「解けない方程式」を解く』ピーター・ペジック著、山下純一訳
　その他
『天才数学者はこう解いた、こう生きた』木村俊一著

を参考にして、「対称性を恒等置換にまで破壊する」という目標を到達点にして、５次以上の方程式には解の公式が存在しないことを証明しました。ガロアによる「群」の概念は登場していませんが、「対称性を破壊していく（絞り込んでいく）」というアイデアを証明の核としたところに、多少なりともガロアの群による証明を参考としています。
　しかし本文の内容は、証明というより、むしろアイデアの解説に近いかもしれません。数学的にはもっと厳密に議論をしていく必要があります。
　なお、本当の意味での厳密な証明は（アーベルの技巧的な式変形を厳密に取り入れるか）、ガロアの創始した『ガロア理論』が必要になります。現代では、古典的なアーベルの証明よりも、より発展的な『ガロア理論』による証明で完全解決とされています。

　ガロアは $${①}$$ 式を使わないで、５次置換そのものの構造に着目しました。それが『群』という概念です。解の置換の群構造に注目して、５次以上の方程式には解の公式が存在しないことを、群という”フィルター”を通すことによって証明しました。
　しかし、これを勉強するには大学レベルの数学が必要です。ガロアの証明については、時間（とモチベーション）があれば解説していきたいですが、大学の教科書のように抽象的にならないように、具体的に分かりやすく解説できないか考察してみます。

（注１）本シリーズ (13) との違い

　３次巡回置換については本シリーズ (14) で初めて登場します。しかし、本シリーズ (13) の段階では３次巡回置換の解説はまだしていないので、３次方定式の解の公式の「条件Ⅱ」については、簡単のために遇置換のままで証明しています。
　具体的には、$${Y}$$（つまりラグランジュ・リゾルベント $${A}$$） に遇置換（ただし恒等置換以外）を作用させると、$${A}$$ は $${\omega}$$ 倍か $${\omega^2}$$ 倍に変化することを証明し、それによって遇置換シンメトリーが破壊されると解説しています（注２）。

　$${(恒等置換以外の遇置換)A=\omega A}$$
または
　$${(恒等置換以外の遇置換)A=\omega^2A}$$

結局、３次置換においては遇置換（$${➀、➁、➂}$$）は３次巡回置換そのものなので、問題はありませんでした（本シリーズ (14)）。$${Y}$$ としてラグランジュ・リゾルベント $${A}$$ を取れることには違いはありません。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)(\alpha     \beta     \gamma)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

　５次方程式においては「遇置換は３次巡回置換で表せる」という定理が本質的に必要になってくるので、３次方程式においても、先に３次巡回置換を解説してから「条件Ⅱ」（３次巡回置換バージョンとして）を提示した方が分かりやすかったかもしれません。その方が５次方程式との関連が見えやすくなりそうです（後で修正するかも）。
　遅ればせながら、ラグランジュ・リゾルベント $${A}$$ に３次巡回置換を作用させると $${\omega}$$ 倍か $${\omega^2}$$ 倍に変化することの証明は（注２）を参照。

（注２）３次巡回置換をラグランジュ・リゾルベントに作用させる（復習）

　ラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
に、遇置換である２つの３次巡回置換
(case1)　$${(\alpha     \gamma     \beta)}$$
(case2)　$${(\alpha     \beta     \gamma)}$$
を作用させます。これによって、(step2) の $${Y}$$ として、ラグランジュ・リゾルベント $${A}$$ を取ればよいことが分かります。

(case1)　$${(\alpha     \gamma     \beta)}$$ を $${A}$$ に作用させる。
　$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に
　$${\alpha \rightarrow \gamma \rightarrow \beta \rightarrow \alpha}$$
と巡回的に置き換えると

$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow\\
&\gamma+\omega\alpha+\omega^2\beta\\
=\,&\underset{1}{\underline{\omega^3}}\,\gamma+\omega\alpha+\omega^2\beta\\
=\,&\omega(\omega^2\gamma+\alpha+\omega\beta)\\
=\,&\omega(\alpha+\omega\beta+\omega^2\gamma)\\
=\,&\omega A
\end{align*}
$$

より

$$
\begin{align*}
(\alpha     \gamma     \beta)A=\omega A　\cdots ⑬
\end{align*}
$$

となり、$${A}$$ は $${\omega A}$$ に変化します。
　所々で $${\omega^3=1}$$ をうまく使います。$${\gamma}$$ に $${\omega^3}$$ をかけるのがポイントです。$${\omega^3}$$ は $${1}$$ なので掛けても式の値は変わりません。また最後に $${\omega}$$ でくくって $${\omega A}$$ を導いています。$${\omega}$$ でくくったときに、$${\alpha}$$ の係数が $${1}$$ になるようにするのもポイントです。
　また、$${(\alpha     \gamma     \beta)}$$ の $${A^3}$$ への作用は、$${A}$$ のみに作用して３乗は変えないので

$$
\begin{align*}
(\alpha     \gamma     \beta)A^3&=(\alpha     \gamma     \beta)A\cdot(\alpha     \gamma     \beta)A\cdot(\alpha     \gamma     \beta)A\\
&=\{(\alpha     \gamma     \beta)A\}^3\\
&=(\omega A)^3　（⑬ を代入）\\
&=\omega^3A^3
\end{align*}
$$

$${\omega^3=1}$$ より

$$
\begin{align*}
(\alpha     \gamma     \beta)A^3&=A^3\\
\end{align*}
$$

となり、$${A^3}$$ は変化しません。

(case2)　$${(\alpha     \beta     \gamma)}$$ を $${A}$$ 作用させる。
　$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に
　$${\alpha \rightarrow \beta \rightarrow \gamma \rightarrow \alpha}$$
と巡回的に置き換えると

$$
\begin{align*}
A=\,&\alpha+\omega\beta+\omega^2\gamma\\
&\hspace{-2pt}\downarrow\hspace{20pt}\downarrow\hspace{24pt}\downarrow\\
&\beta+\omega\gamma+\omega^2\alpha\\
=\,&\underset{1}{\underline{\omega^3}}\,\beta+\underset{1}{\underline{\omega^3}}\cdot\omega\gamma+\omega^2\alpha\\
=\,&\omega^3\beta+\omega^4\gamma+\omega^2\alpha\\
=\,&\omega^2(\omega\beta+\omega^2\gamma+\alpha)\\
=\,&\omega^2(\alpha+\omega\beta+\omega^2\gamma)=\omega^2A\\
\end{align*}
$$

より

$$
\begin{align*}
(\alpha     \beta     \gamma)A=\omega^2A　\cdots ⑭
\end{align*}
$$

となり、$${A}$$ は $${\omega^2A}$$ に変化します。
　ここでも所々で $${\omega^3=1}$$ を使います。$${\omega^3}$$ は $${1}$$ なので掛けても式の値は変わりません。また最後に $${\omega^2}$$ でくくって $${\omega^2A}$$ を導きます。ここでも $${\omega^2}$$ でくくったときに、$${\alpha}$$ の係数が $${1}$$ になるようにするのがポイントです。
　また、$${(\alpha     \gamma     \beta)}$$ の $${A^3}$$ への作用は、$${A}$$ のみに作用して３乗は変えないので

$$
\begin{align*}
(\alpha     \beta     \gamma)A^3&=(\alpha     \beta     \gamma)A\cdot(\alpha     \beta     \gamma)A\cdot(\alpha     \beta     \gamma)A\\
&=\{(\alpha     \beta     \gamma)A\}^3\\
&=\{\omega^2A\}^3　（⑭ を代入）\\
&=(\omega^2)^3A^3\\
&=\omega^6A^3
\end{align*}
$$

$${\omega^6=(\underset{1}{\underline{\omega^3}})^2=1^2=1}$$ より

$$
\begin{align*}
(\alpha     \gamma     \beta)A^3&=A^3\\
\end{align*}
$$

となり、$${A^3}$$ は変化しません。
　以上により、(step2) の $${Y}$$ として、ラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
を取ればよいことが分かりました。

（注３）『背理法』について（復習）

　『背理法』とは、「ある命題の結論が正しいことを証明するために、その結論の否定を仮定して、すでに真であるとわかっている事実や元の命題の仮設などに矛盾することから、その命題の結論が正しいことを証明する方法」
　例えば次の命題を背理法で証明しましょう。
命題『ある整数 $${n}$$ について $${n^2}$$ が偶数であるとする。このとき $${n}$$ は偶数である。』
（証明）
　この命題の結論は「$${n}$$ は偶数である」。この結論の否定、つまり「$${n}$$ は奇数である」と仮定する（背理法の仮定）。$${n}$$ は奇数なので、$${k}$$ を $${0}$$ 以上の整数 ($${0, 1, 2, 3, \cdots}$$) として $${n=2k+1}$$ とおける *。
　ここで展開公式
　$${(a+b)^2=a^2+2ab+b^2}$$
を用いると

$$
\begin{align*}
n^2&=(2k+1)^2\\
&=(2k)^2+2\cdot2k\cdot1+1^2\\
&=4k^2+4k+1\\
&=2(2k^2+2k)+1\\
&=2l+1 （ただし  l=2k^2+2k  とおいた）
\end{align*}
$$

すると、$${k}$$ は $${0}$$ 以上の整数であることから、$${l(=2k^2+2k)}$$ も $${0}$$ 以上の整数となるので、 $${2l+1}$$ は奇数である*。これは $${n^2}$$ が偶数であるという条件（元の命題の仮設）に矛盾しているので、これによって背理法の仮定「$${n}$$ は奇数である」が正しくないこと、つまり「$${n}$$ は偶数である」ことが証明された。（証明終）

＊奇数 $${1,  3,  5,  7, \cdots}$$ は
　$${1=2\times0+1}$$
　$${3=2\times1+1}$$
　$${5=2\times2+1}$$
　$${7=2\times3+1}$$
$${\hspace{23pt}\vdots}$$
より、$${n=2k+1}$$（$${k}$$ は $${0}$$ 以上の整数）の形で書ける。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について