ガロアは『群』という数学的概念を用いて、５次以上の方程式に解の公式が存在しないことを証明しました。ここでは、その『群』について簡単に解説します。
（追記）あまり推敲せず、厳密でないところがあるので修正しました。分かりやすさと厳密性の狭間でもがいております。現状アバウトに読んでください。

集合について

　数学的な意味での集合とは「範囲のはっきりしたものの集まり」です。そして集合を作っている個々のものを、その集合の要素といいます。要素のことを元という場合もあります。
　例えば、自然数の集合や、$${24}$$ の正の約数の集合などは、数学的な意味での集合となります。
　要素を並べて書くと、自然数の集合は
　$${\{1,  2,  3,  4,  5,  \cdots\}}$$
　$${24}$$ の正の約数の集合は
　$${\{1,  2,  3,  4,  6,  8,  12,  24\}}$$
となります。
　要素が無限個の集合を『無限集合』、要素が有限個の集合を『有限集合』といいます。自然数の集合は『無限集合』、$${24}$$ の正の約数の集合は『有限集合』です。無限集合は要素をすべて並べることはできないので、「$${\cdots}$$」という記号を用いて表します。

　さてここで、整数全体の集合 $${\mathbb{Z}}$$ を考えます。この記号 $${\mathbb{Z}}$$ はドイツ語で数を表す「Zahlen」、あるいは整数を表す「Ganze Zahl」が由来とされています。その整数全体の集合 $${\mathbb{Z}}$$ を要素を並べて書くと、次のようになります。

$$
\begin{align*}
\mathbb{Z}=\{\cdots,  -3.  -2.  -1,   0,   1,   2,   3,  \cdots\}
\end{align*}
$$

　ここで、新しい記号を導入します。$${a}$$ が集合 $${S}$$ の要素であることを

$$
\begin{align*}
a \in S
\end{align*}
$$

$${a}$$ が集合 $${S}$$ の要素でないことを

$$
\begin{align*}
a \notin S
\end{align*}
$$

と表します。$${1}$$ は整数の集合 $${\mathbb{Z}}$$ の要素であるので

$$
\begin{align*}
1 \in \mathbb{Z}
\end{align*}
$$

$${-2}$$ も $${0}$$ も整数の集合 $${\mathbb{Z}}$$ の要素なので

$$
\begin{align*}
-2 &\in \mathbb{Z}\\
0 &\in \mathbb{Z}
\end{align*}
$$

となります。一方、分数 $${\dfrac{3}{2}}$$ や、無理数 $${\sqrt{2}}$$ は整数ではないので

$$
\begin{align*}
\dfrac{3}{2} &\notin \mathbb{Z}\\[6pt]
\sqrt{2} &\notin \mathbb{Z}
\end{align*}
$$

となります。
　集合の概念を扱うことで、中身（要素）が無限にある集合でも、数学的対象として扱いやすくなります。
　無限にある集合を、輪郭のある”袋”（整数 $${\mathbb{Z}}$$ という袋）のようなイメージでとらえることができるので、その袋に入っている、入ってい

ないで、厳密な数学的議論が可能になります。

群について

　ここで、整数の集合 $${\mathbb{Z}}$$ は次のような性質 (1)～(4) をもちます。

(1)　$${\mathbb{Z}}$$ から任意の（自由に）２つの要素を選んで足したとき、それは $${\mathbb{Z}}$$ に含まれる。平たくいえば、整数同士を足しても整数である。
　例えば、$${1}$$ と $${2}$$ を足すと整数、$${4}$$ と $${-6}$$ を足しても整数です。
　$${1+2=3（整数）}$$
　$${4+(-6)=-2（整数）}$$
整数同士をたして、例えば分数 $${\dfrac{3}{2}}$$ や、無理数 $${\sqrt{2}}$$ になることはありません。このことを、整数全体の集合はたし算について閉じているといいます。

(2)　結合法則がなりたつ。
　結合法則とは、任意の整数 $${a,  b,  c}$$ について
　$${(a+b)+c=a+(b+c)}$$
が成り立つことです。例えば
　$${(1+2)+3=1+(2+3)}$$
が成り立ちます。これは $${1+2+3}$$ について、$${{1+2}}$$ を先に計算してから $${3}$$ を足しても、$${2+3}$$ を先に計算してから $${1}$$ を足しても、その結果は同じになるという法則です。実際
　（左辺）=$${(1+2)+3=3+3=6}$$
　（右辺）=$${1+(2+3)=1+5=6}$$
より、どちらも $${6}$$ になります。
　これによって、たし算に関してどこから計算しても同じ値となることが保証されます。
　$${1+2+3}$$
とあった場合、どこから足してもよいということです。
　この法則を認めると、例えば４つの任意の整数 $${a,  b,  c}$$ について

$$
\begin{align*}
\{(a+b)+c\}+d=a+\{b+(c+d)\}
\end{align*}
$$

のような結合法則も、以下のように証明できます。

（証明）

$$
\begin{alignat*}{2}
（左辺）&=\{(a+b)+c\}+d & &\\
&=(X+c)+d & &（a+b=X  とおく）\\
&=X+(c+d) & &（分配法則より）\\
&=(a+b)+(c+d) & &（X  を戻す）\\
&=(a+b)+Y & &（c+d=X  とおく）\\
&=a+(b+Y) & &（分配法則より）\\
&=a+\{b+(c+d)\} & &（Y  を戻す）\\
&=（右辺）
\end{alignat*}
$$

　一般に複数の数のたし算があった場合、交換法則を反復して適用することによって、カッコがどのように挿入されているかを気にすることなく、どこから計算しても同じ値となることが保証されます。

(3)　左右両側から足しても変化させない要素が $${\mathbb{Z}}$$ に存在する。
　これは $${0}$$ です。任意の整数に、両側から $${0}$$ を足しても変化しません。例えば
　$${1+0=0+1=1}$$（変化しない）
　$${-4+0=0+(-4)=-4}$$（変化しない）
右から、左から、どちらから $${0}$$ をたしても $${1}$$ は $${1}$$ のまま、$${-4}$$ は $${-4}$$ のままで変化しません。この $${0}$$ を『単位元』といいます。

(4)　任意の整数に両側から足すと『単位元』$${0}$$ となるような要素が $${\mathbb{Z}}$$ に存在する。
　例えば、整数 $${2}$$ に対しては
　$${2+\underline{(-2)}=\underline{(-2)}+2=0}$$（単位元）
より、左右両側から $${\underline{-2}}$$ を足すと単位元 $${0}$$ となるので、その要素は $${-2}$$ です。
　整数 $${-5}$$ に対しては
　$${(-5)+\underline{5}=\underline{5}+(-5)=0}$$（単位元）
より、その要素は $${\underline{5}}$$ です。この要素を『逆元』といいます。逆元は、その要素によって変わります。
例　$${2}$$ の逆元は $${-2}$$
　　$${-5}$$ の逆元は $${5}$$
　　$${0}$$ の逆元は $${0}$$

　この (1)～(4) をすべて満たす集合を『群』といいます。これを大学の教科書に書かれている形で表現すると、次のようになります。先ほどの整数の性質を抽出して、それを群の定義として、記号を使って書き並べたものです。いきなり抽象的になりますが、具体的に解説します。

群の定義

　空でない集合 $${G}$$ の任意の要素 $${a,  b,  c}$$ の間に１つの演算 $${*}$$ が規定されているとする。
　この集合 $${G}$$ の任意の要素 $${a,  b,  c}$$ が、その演算 $${*}$$ に関して次の条件を満たすとき、$${G}$$ は演算 $${*}$$ に関して群であるという。
(1)　$${a*b}$$ は $${G}$$ の要素である。
(2)　交換法則 $${(a*b)*c=a*(b*c)}$$ が成り立つ。
(3)　$${a*e=e*a=a}$$ となる単位元 $${e}$$ が $${G}$$ に存在する。
(4)　$${a*x=x*a=e}$$ となる逆元 $${x}$$ が $${G}$$ に存在する。

＊＊＊

(1) を満たすことを、集合 $${\bm G}$$ は演算 $${\bm *}$$ について閉じているといいます。演算の結果、集合 $${G}$$ からはみ出さないことを意味します。
(2) は、カッコを気にしないで、どこから演算を施してもよいことを保証します。
(3) は、左右どちらから演算を施しても変化しない要素の存在です。この要素を単位元といいます。
(4) は、左右両方から演算を施すと単位元になるような要素の存在です。この要素を逆元といいます。
　単なる集合（要素の集まり）ではなく、集合の要素に、上記の演算規則 (1)～(4) が規定された集合が群です。

　要するに群とは、イメージとして
(1)　全部そろっている
(2)　つなげることができる
(3)　変えないことができる
(4)　元に戻すことができる
の４つの条件が成り立つもの（要素）の集まり（集合）です。

　この定義にそって先ほどの整数の集合を考えると、$${G}$$ が整数の集合 $${\mathbb{Z}}$$ に相当し、演算 $${*}$$ がたし算 $${+}$$ に相当します。
　すると、集合 $${\mathbb{Z}}$$ の任意の要素 $${a,  b,  c}$$ が、たし算に関して先ほどの群の条件

(1)　$${a+b}$$ は $${\mathbb{Z}}$$ の要素である。
(2)　交換法則 $${(a+b)+c=a+(b+c)}$$ が成り立つ。
(3)　$${a+0=0+a=a}$$ となる単位元 $${0}$$ が存在する。
(4)　$${a+x=x+a=e}$$ となる逆元 $${x}$$ が存在する。

をすべて満たすので、$${\mathbb{Z}}$$ がたし算に関して群になることが分かります。
　群の定義は抽象的ですが、その抽象性によって、さまざまな演算を統一的に扱えるというメリットがあります。本記事のテーマですが、３次置換の集合も群になるということです。後にこのことを証明します。

群にはならない例

　先ほどみたように、$${\mathbb{Z}}$$ はたし算に関して群になることが分かりました。
　それでは演算をたし算からかけ算にかえて、$${\mathbb{Z}}$$ はかけ算 $${\times}$$ に関して 群になるでしょうか？
　集合 $${\mathbb{Z}}$$ の任意の要素 $${a,  b,  c}$$ が、かけ算に関して群の定義 (1)～(4) をすべて満たすかどうか、順にチェックしていきます。「かけ算に関して」なので、行う演算は当然かけ算です。

(1)　$${a\times b}$$ は $${G}$$ に属する。
　整数に整数を掛けても整数なので成り立ちます。
例　$${2\times3=5（整数）}$$
　　$${-5\times4=-20（整数）}$$

(2)　交換法則 $${(a\times b)\times c=a\times(b\times c)}$$ が成り立つ。
　かけ算に関して、交換法則は成り立ちます。
例　$${(2\times3)\times5=2\times(3\times5)}$$
　　$${\{3\times(-4)\}\times(-2)=3\times\{(-4)\times(-2)\}}$$

(3)　左右両側から掛けても変化しない要素（単位元）が存在する。
　$${1}$$ は両側から掛けても変化しないので、$${1}$$ が単位元となります。
例　$${2\times1=1\times2=2}$$（変化しない）
　より $${1}$$ が単位元

(4)　左右両側から掛けると単位元となる要素（逆元）が存在する。
　しかし、逆元は存在しません。例えば整数 $${2}$$ について考えると
　$${2\times x=x\times2=1}$$（単位元）
となる $${x}$$ は、整数の範囲では存在しません。計算上は $${x}$$ として $${\dfrac{1}{2}}$$ を取ればよいように思えますが、$${\dfrac{1}{2}}$$ は整数ではないので、逆元は存在しないことになります。

　以上により、条件 (4) を満たしていないので、$${\mathbb{Z}}$$ はかけ算に関して群にならないことが分かりました。
　同じ集合 $${\mathbb{Z}}$$ でも、演算としてたし算を考えた場合は群になりますが、かけ算を考えた場合は群になりません。同じ集合でも、どのような演算を考えるかによって群になったり、群にならなかったりします。その集合が群であるかどうかは、どのような演算を考えているかによるのです。

３次置換について（復習）

　実は、３次置換の集合は、置換の作用という演算に関して群になります。ガロアの発見した群の概念です。後に詳しく解説するために、３次置換について復習します。
　３次置換には以下の６種類があり、遇置換は３次巡回置換、奇置換は互換で表すことができます（本シリーズ (14)）。なお、互換は２つの文字の巡回置換（２次巡回置換）とみなすことができます。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

　ここでは、便宜的にギリシャ文字 $${\rho}$$（ロウ）、$${\tau}$$（タウ）を用いて、次のように置き換えます。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I=id(=\rho_1)\\
\\
➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha     \gamma     \beta)
=\rho_2\\
\\
➂\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha     \beta     \gamma)
=\rho_3
\end{rcases}遇置換\\
\\
&\begin{rcases}
➃\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}=\tau_1\\
\\
➄\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}=\tau_2\\
\\
➅\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}=\tau_3
\end{rcases}奇置換
\end{align*}
$$

➀  は同じもの同士を入れ替える置換（変化しない）
➁  は
　$${\alpha \rightarrow \gamma \rightarrow \beta \rightarrow \alpha}$$
とサイクリックに入れ替える３次巡回置換
➂  は
　$${\alpha \rightarrow \beta \rightarrow \gamma \rightarrow \alpha}$$
とサイクリックに入れ替える３次巡回置換
➃  は
　$${\beta \rightarrow \gamma \rightarrow \beta}$$
とサイクリックに入れ替える２次巡回置換（$${\alpha}$$ は変化しない）
➄  は
　$${\gamma \rightarrow \alpha \rightarrow \gamma}$$
とサイクリックに入れ替える２次巡回置換（$${\beta}$$ は変化しない）
➅ は
　$${\alpha \rightarrow \beta \rightarrow \alpha}$$
とサイクリックに入れ替える２次巡回置換（$${\gamma}$$ は変化しない）

　これらを文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
➀   id\hspace{5pt}&\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma
\end{align*}
\hspace{10pt}
\begin{align*}
➁   \rho_2\hspace{5pt}&\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta
\end{align*}
\hspace{10pt}
\begin{align*}
➂   \rho_2\hspace{5pt}&\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha
\end{align*}
$$

$$
\begin{align*}
➃   \tau_1\hspace{5pt}&\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\underset{不変}{\alpha}\hspace{-4pt}     &\gamma     \beta
\end{align*}
\hspace{10pt}
\begin{align*}
➄   \tau_2\hspace{5pt}&\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma\hspace{-1pt}     &\hspace{-2pt}\underset{不変}{\beta}      \hspace{-4pt}\alpha
\end{align*}
\hspace{10pt}
\begin{align*}
➅   \tau_3\hspace{5pt}&\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \hspace{-3pt}\underset{不変}{\gamma}
\end{align*}
$$

　なお、$${id}$$ は単位元（identity element）を省略した記号です。後で述べますが、恒等置換 $${I}$$ は作用させても変化しない置換なので、群として単位元となります。
　また、通し番号として $${id}$$ は $${\rho_1}$$ とおくことも可能ですが、作用させても変化しない特別な置換なので、他とは違う記号 $${id}$$ を用います。

置換の合成（積）

　$${\rho_2\circ\tau_3}$$ は、置換 $${\rho_2}$$ の後に置換 $${\tau_3}$$ を作用させることを意味します。これを置換の合成、または置換の積といいます。本シリーズでは置換の積の方を主に使います。
　なお、本シリーズでは、置換は前から作用すると定義します。大学の教科書では後ろから定義するのが一般的ですが、分かりやすさのため、ここでは前から（左から）作用させるとします。
　例えば $${\rho_2\circ\tau_3}$$ とあれば、それは先に $${\rho_2}$$ を作用させ、後に $${\tau_3}$$ を作用させます。

$$
\begin{align*}
\underset{先}{\rho_2}\circ\underset{後}{\tau_3}
\end{align*}
$$

　具体的に、この $${\rho_2\circ\tau_3}$$ は

$$
\begin{align*}
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　{\small \rho_2=(\alpha     \gamma     \beta)  を作用}\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　{\small \tau_3=(\alpha     \beta)  を作用}\\
\gamma     &\beta     \alpha
\end{align*}
$$

より、初めと最後をつなげて

$$
\begin{align*}
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow\\
\gamma     &\beta     \hspace{-1pt}\alpha 
\end{align*}
$$

となります。これは３次置換のうち、⑤ の置換である
　$${(\alpha     \gamma)=\tau_2}$$
と等しくなります。

$$
\begin{align*}
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　{\small \tau_2=(\alpha     \gamma)  を作用}\\
\gamma     &\beta     \hspace{-1pt}\alpha 
\end{align*}
$$

　なお、今後は $${\rho_2\circ\tau_3}$$ の「$${\circ}$$」は書かないで、単に $${\rho_2\tau_3}$$ と書いていきます。先ほどの例だと
　$${\rho_2\tau_3=\tau_2}$$
となります。

３次置換を回転と反転でとらえる

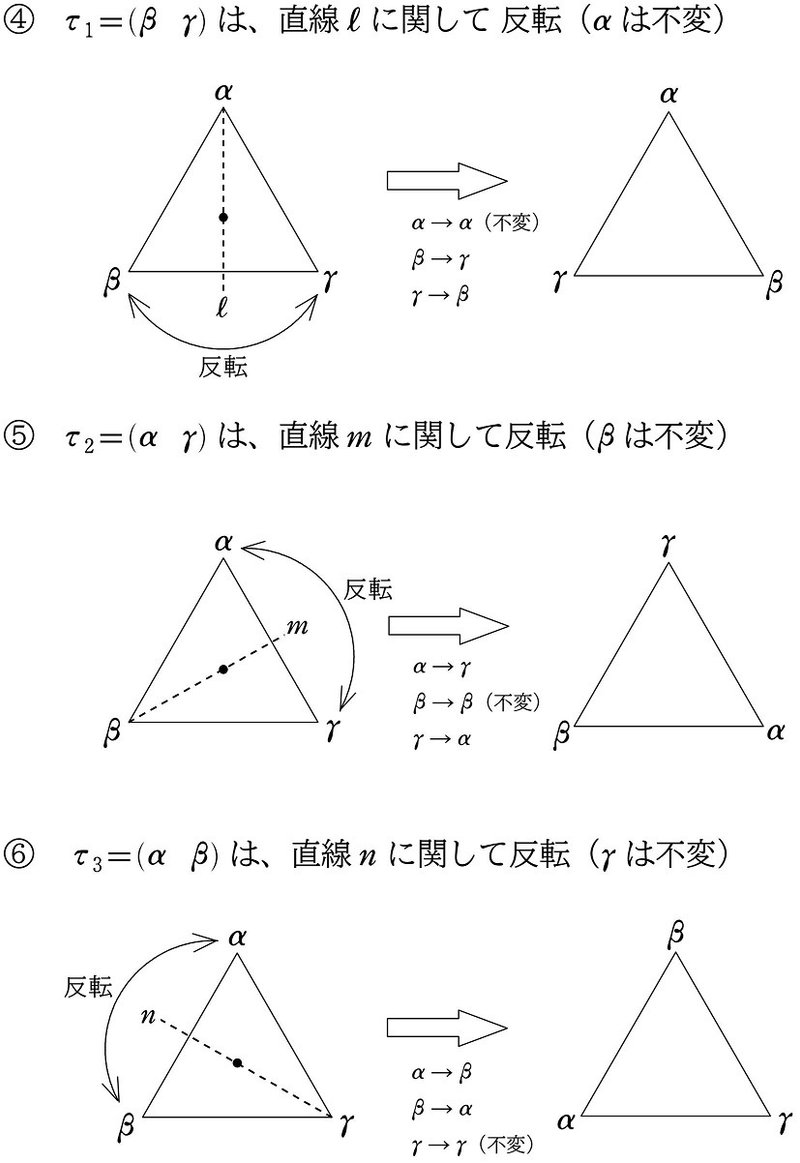
　また、これらの置換は、下図のように三角形の「回転」と「反転」でとらえるとイメージしやすくなります。 $${\alpha,  \beta,  \gamma}$$ を頂点にもつ三角形について
➀  は $${0^\circ}$$ 回転（変化しない）
➁  は反時計回りに $${120^\circ}$$ 回転
➂  は反時計回りに $${240^\circ}$$ 回転
➃  は $${\beta}$$ と $${\gamma}$$ の反転（$${\alpha}$$ を固定）
➄ は $${\alpha}$$ と $${\gamma}$$ の反転（$${\beta}$$ を固定）
➅  は $${\alpha}$$ と $${\beta}$$ の反転（$${\gamma}$$ を固定）
と捉えます。
　遇置換である①～③は（回転しないことも含めて）「回転」グループ、奇置換である ④～➅は「反転」グループと分けることが可能です。

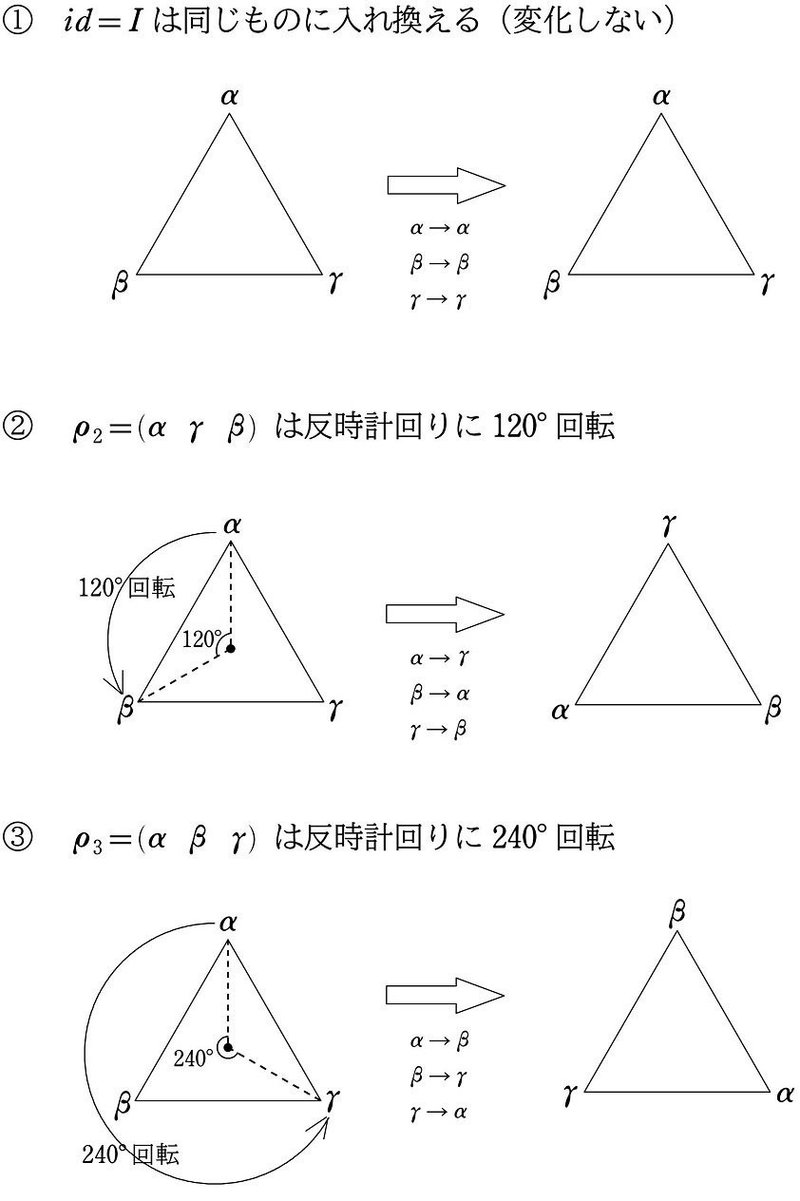
　例えば ② について、$${120^\circ}$$ 回転によって、$${\alpha}$$ の地点に $${\gamma}$$ が配置され、$${\gamma}$$ の地点に $${\beta}$$ が配置され、$${\beta}$$ の地点に $${\alpha}$$ が配置されることから、この回転を表す置換は
　$${\rho_2=(\alpha     \gamma     \beta)}$$
となります。
　すると、例えば $${\rho_2\tau_3}$$ は、$${120^\circ}$$ 回転 ($${\rho_2}$$) させてから、$${\alpha}$$ と $${\beta}$$ を反転 ($${\tau_3}$$) させることを意味します。この置換の積は、$${\alpha}$$ と $${\gamma}$$ の反転 $${\tau_2}$$ と同じ置換になります。

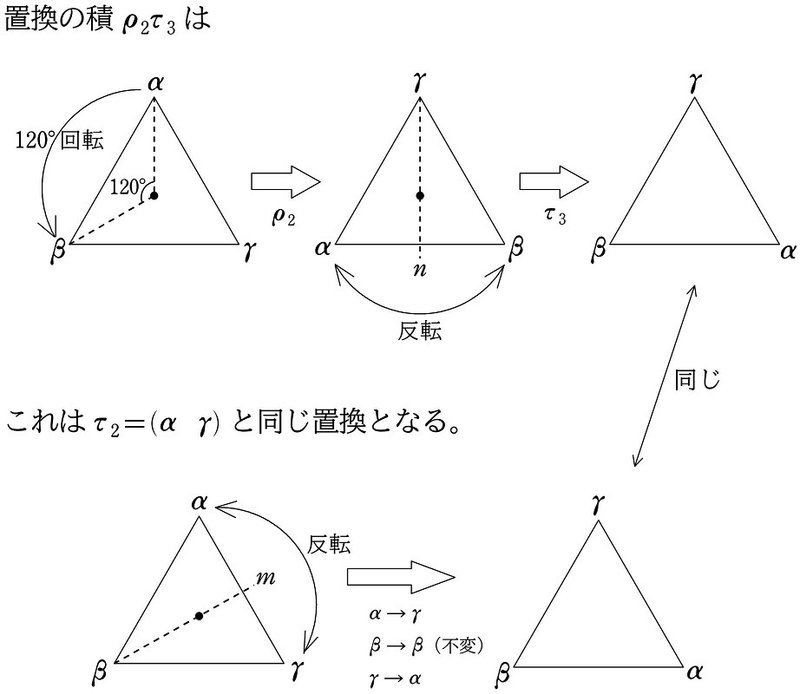
つまり

$$
\begin{align*}
\rho_2\tau_3=\tau_2
\end{align*}
$$

３次対称群について

　ここで、３次置換のすべての集合を $${S_3}$$ とします。つまり
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
です。この集合は、置換の積 $${\circ}$$ という演算に関して群になります。この群を『３次対称群』といいます。
　では、この３次対称群が、置換の積に関して群の定義 (1)～(4) を満たしていることを確認していきます。

３次置換の集合が群であることの証明

(1)　任意の２つの要素の積も、その集合の要素になる。

　$${S_3}$$ の任意の２つの要素の積は $${S_3}$$ の要素になります。
　$${S_3}$$ の要素は全部で $${6}$$ 通りあるので、その置換の積は全部で $${6\times6=36}$$ 通りあります。その $${36}$$ 通りのすべてが $${S_3}$$ の要素になること、つまり $${S_3}$$ からはみ出さないことを具体的に示していきます。

(a)　先に $${id}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。$${id}$$ は恒等置換なので、いずれも変化しません。

(a1)　$${idid=id}$$
(a2)　$${id\rho_2=\rho_2}$$
(a3)　$${id\rho_3=\rho_3}$$
(a4)　$${id\tau_1=\tau_1}$$
(a5)　$${id\tau_2=\tau_2}$$
(a6)　$${id\tau_3=\tau_3}$$

　(a1)～(a6) は、すべて $${S_3}$$ の要素になります。実際に文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
\text{(a1)}    id &id=id\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(a2)}    id &\rho_2=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(a3)}    id &\rho_3=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha
\end{align*}
$$

$$
\begin{align*}
\text{(a4)}    id &\tau_1=\tau_1\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(a5)}    id &\tau_2=\tau_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(a6)}    id &\tau_3=\tau_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma
\end{align*}
$$

　結果は、初めと最後をつなげます。例えば (a2) は

$$
\begin{align*}
\text{(a2)}    id &\rho_2=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta
\end{align*}
$$

より、$${id\rho_2=\rho_2}$$ となります。
　この結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{2pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
    & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\
\end{array}
\begin{array}{c}
\\
← \text{(a)}
\end{array}
$$

(b)　先に $${\rho_2}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。

(b1)　$${\rho_2id=\rho_2}$$
(b2)　$${\rho_2\rho_2=\rho_3}$$
(b3)　$${\rho_2\rho_3=id}$$
(b4)　$${\rho_2\tau_1=\tau_3}$$
(b5)　$${\rho_2\tau_2=\tau_1}$$
(b6)　$${\rho_2\tau_3=\tau_2}$$

　(b1)～(b6) は、すべて $${S_3}$$ の要素になります。実際に文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
\text{(b1)}    \rho_2 &id=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　id  を作用\\
\gamma     &\alpha     \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(b2)}    \rho_2 &\rho_2=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\beta     &\gamma     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(b3)}    \rho_2 &\rho_3=id\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\alpha     &\beta     \gamma
\end{align*}
$$

$$
\begin{align*}
\text{(b4)}    \rho_2 &\tau_1=\tau_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\beta     &\alpha     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(b5)}    \rho_2 &\tau_2=\tau_1\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\alpha     &\gamma     \beta 
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(b6)}    \rho_2 &\tau_3=\tau_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\alpha     \beta\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\gamma     &\beta     \alpha
\end{align*}
$$

　結果は、初めと最後をつなげます。例えば (b2) は

$$
\begin{align*}
\text{(b2)}    \rho_2 &\rho_2=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha
\end{align*}
$$

より、$${\rho_2\rho_2=\rho_3}$$ となります。以下同様です。
　これまでの結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{3pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
    & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2
\end{array}
\begin{array}{c}
\\
← \text{(a)}\\
← \text{(b)}
\end{array}
$$

(c)　先に $${\rho_3}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。

(c1)　$${\rho_3id=\rho_3}$$
(c2)　$${\rho_3\rho_2=id}$$
(c3)　$${\rho_3\rho_3=\rho_2}$$
(c4)　$${\rho_3\tau_1=\tau_2}$$
(c5)　$${\rho_3\tau_2=\tau_3}$$
(c6)　$${\rho_3\tau_3=\tau_1}$$

　(c1)～(c6) は、すべて $${S_3}$$ の要素になります。実際に文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
\text{(c1)}    \rho_3 &id=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha\\
&\hspace{-2pt}\downarrow　id  を作用\\
\beta     &\gamma     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(c2)}    \rho_3 &\rho_2=id\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\alpha     &\beta     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(c3)}    \rho_3 &\rho_3=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\gamma     &\alpha     \beta
\end{align*}
$$

$$
\begin{align*}
\text{(c4)}    \rho_3 &\tau_1=\tau_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\gamma     &\beta     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(c5)}    \rho_3 &\tau_2=\tau_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\beta     &\alpha     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(c6)}    \rho_3 &\tau_3=\tau_1\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\gamma     \alpha\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\alpha     &\gamma     \beta
\end{align*}
$$

　これまでの結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{3pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
    & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1
\end{array}
\begin{array}{c}
\\
\leftarrow (a)\\
\leftarrow (b)\\
\leftarrow (c)
\end{array}
$$

(d)　先に $${\tau_1}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。

(d1)　$${\tau_1id=\tau_1}$$
(d2)　$${\tau_1\rho_2=\tau_2}$$
(d3)　$${\tau_1\rho_3=\tau_3}$$
(d4)　$${\tau_1\tau_1=id}$$
(d5)　$${\tau_1\tau_2=\rho_2}$$
(d6)　$${\tau_1\tau_3=\rho_3}$$

　(d1)～(d6) は、すべて $${S_3}$$ の要素になります。実際に文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
\text{(d1)}    \tau_1 &id=\tau_1\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta\\
&\hspace{-2pt}\downarrow　id  を作用\\
\alpha     &\gamma     \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(d2)}    \tau_1 &\rho_2=\tau_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\gamma     &\beta     \alpha 
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(d3)}    \tau_1 &\rho_3=\tau_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\beta     &\alpha     \gamma
\end{align*}
$$

$$
\begin{align*}
\text{(d4)}    \tau_1 &\tau_1=id\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\beta     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(d5)}    \tau_1 &\tau_2=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\alpha     \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(d6)}    \tau_1 &\tau_3=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\alpha     &\gamma     \beta\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\gamma     \alpha
\end{align*}
$$

　これまでの結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{1pt}後\\
\raisebox{-10pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
    & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3
\end{array}
\begin{array}{c}
\\
\leftarrow (a)\\
\leftarrow (b)\\
\leftarrow (c)\\
\leftarrow (d)
\end{array}
$$

(e)　先に $${\tau_2}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。

(e1)　$${\tau_2id=\tau_2}$$
(e2)　$${\tau_2\rho_2=\tau_3}$$
(e3)　$${\tau_2\rho_3=\tau_1}$$
(e4)　$${\tau_2\tau_1=\rho_3}$$
(e5)　$${\tau_2\tau_2=id}$$
(e6)　$${\tau_2\tau_3=\rho_2}$$

　(e1)～(e6) は、すべて $${S_3}$$ の要素になります。実際に文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
\text{(e1)}    \tau_2 &id=\tau_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha\\
&\hspace{-2pt}\downarrow　id  を作用\\
\gamma     &\beta     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(e2)}    \tau_2 &\rho_2=\tau_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\beta     &\alpha      \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(e3)}    \tau_2 &\rho_3=\tau_1\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\alpha     &\gamma     \beta
\end{align*}
$$

$$
\begin{align*}
\text{(e4)}    \tau_2 &\rho_2=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\beta     &\gamma     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(e5)}    \tau_2 &\tau_2=id\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\alpha     &\beta     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(e6)}    \tau_2 &\tau_3=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\gamma     &\beta     \alpha\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\gamma     &\alpha     \beta
\end{align*}
$$

　これまでの結果を表にまとめると、次のようになります。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{1pt}後\\
\raisebox{-11pt}{先}
\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
    & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3 \\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2 & \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2
\end{array}
\begin{array}{c}
\\
\leftarrow (a)\\
\leftarrow (b)\\
\leftarrow (c)\\
\leftarrow (d)\\
\leftarrow (e)
\end{array}
$$

(f)　先に $${\tau_3}$$ を作用し、次に３次対称群のすべての要素を作用させると、結果は次のようになります。

(f1)　$${\tau_3id=\tau_3}$$
(f2)　$${\tau_3\rho_2=\tau_1}$$
(f3)　$${\tau_3\rho_3=\tau_2}$$
(f4)　$${\tau_3\tau_1=\rho_2}$$
(f5)　$${\tau_3\tau_2=\rho_3}$$
(f6)　$${\tau_3\tau_3=id}$$

　(f1)～(f6) は、すべて $${S_3}$$ の要素になります。実際に文字列 $${\alpha     \beta     \gamma}$$ に作用させると

$$
\begin{align*}
\text{(f1)}    \tau_3 &id=\tau_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma\\
&\hspace{-2pt}\downarrow　id  を作用\\
\beta     &\alpha     \gamma
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(f2)}    \tau_3 &\rho_2=\tau_1\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma\\
&\hspace{-2pt}\downarrow　\rho_2  を作用\\
\alpha     &\gamma      \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(f3)}    \tau_3 &\rho_3=\tau_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma\\
&\hspace{-2pt}\downarrow　\rho_3  を作用\\
\gamma     &\beta     \alpha
\end{align*}
$$

$$
\begin{align*}
\text{(f4)}    \tau_3 &\rho_2=\rho_2\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma\\
&\hspace{-2pt}\downarrow　\tau_1  を作用\\
\gamma     &\alpha     \beta
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(f5)}    \tau_3 &\tau_2=\rho_3\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma\\
&\hspace{-2pt}\downarrow　\tau_2  を作用\\
\beta      &\gamma     \alpha
\end{align*}
\hspace{5pt}
\begin{align*}
\text{(f6)}    \tau_3 &\tau_3=id\\
\alpha     &\beta     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\beta     &\alpha     \gamma\\
&\hspace{-2pt}\downarrow　\tau_3  を作用\\
\alpha     &\beta     \gamma
\end{align*}
$$

　この結果を表にまとめると、次のようになります。先ほどの (a)～(e) の結果に (f) の結果を加えていきます。先に作用させる置換を縦に、後に作用させる置換を横に並べています。

$$
\def\arraystretch{1.5}
\hspace{1pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c|c|c|c|c}
    & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline\hline
id & id & \rho_2 & \rho_3 & \tau_1 & \tau_2 & \tau_3\\ \hline
\rho_2 & \rho_2 & \rho_3 & id & \tau_3 & \tau_1 & \tau_2\\ \hline
\rho_3 & \rho_3 & id & \rho_2& \tau_2 & \tau_3 & \tau_1\\ \hline
\tau_1 & \tau_1 & \tau_2 & \tau_3 & id & \rho_2 & \rho_3\\ \hline
\tau_2 & \tau_2 & \tau_3 & \tau_1 & \rho_3 & id & \rho_2\\ \hline
\tau_3 & \tau_3 & \tau_1 & \tau_2 & \rho_2 & \rho_3 & id
\end{array}
\begin{array}{c}
\\
\leftarrow (a)\\
\leftarrow (b)\\
\leftarrow (c)\\
\leftarrow (d)\\
\leftarrow (e)\\
\leftarrow (f)
\end{array}
$$

　これで表が完成しました。表内の $${6\times6=36}$$ 通りのすべての要素は $${S_3}$$ に含まれるので、これで群の条件①を満たすことが示されます。
　３次置換 $${S_3}$$ は「回転」と「反転」とみなせるので、この操作の積で得られる結果も、「回転」と「反転」のどれかになることはイメージできると思います。
　続いて、群の条件②～④を満たすことを確認していきます。

(2)　結合法則は成り立つ。

　一般に結合法則は成り立ちます。
例　$${(\rho_2\tau_1)\tau_3=\rho_2(\tau_1\tau_3)}$$
　任意の要素に対して成り立つので、同じ置換を用いても構いません。
　　$${(\rho_2\tau_1)\rho_2=\rho_2(\tau_1\rho_2)}$$
どこから置換を作用させても、同じ結果となります。

(3)　単位元は存在する。

　　置換の積で、変化しないのが単位元です。
例　$${\rho_2\underline{id}=\underline{id}\rho_2=\rho_2}$$（変化しない）
　　$${\tau_3\underline{id}=\underline{id}\tau_3=\tau_3}$$（変化しない）
　下線部の $${id}$$ が単位元です。
　このように、単位元は $${S_3}$$ に存在します。

(4)　逆元は存在する。

　置換の積で、単位元 $${id}$$ になるのが逆元です。
例　$${\rho_2}$$ については
　$${\rho_2\underline{\rho_3}=\underline{\rho_3}\rho_2=id}$$（単位元）
より、下線部 $${\rho_3}$$ が逆元となります。
　置換を回転とみなすと、$${\rho_2}$$ は $${120^\circ}$$ 回転、$${\rho_3^\circ}$$ は $${240^\circ}$$ 回転なので、それらを連続して回転させると $${360^\circ}$$ になり、元に戻る（$${id}$$ になる）というイメージです。
例　$${\tau_1}$$ については
　$${\tau\underline{\tau_1}=\underline{\tau_1}\tau_1=id}$$（単位元）
より、下線部 $${\tau_1}$$ が逆元です。
　このように、すべての要素に対して逆元が存在します。
　$${\tau_1}$$ は反転とみなすことができ、反転させたあと、再び同じ反転をすると元に戻る（$${id}$$ になる）というイメージです。
　まとめると
　$${id}$$ の逆元は $${id}$$
　$${\rho_2}$$ の逆元は $${\rho_3}$$
　$${\rho_3}$$ の逆元は $${\rho_2}$$
　$${\tau_1}$$ の逆元は $${\tau_1}$$
　$${\tau_2}$$ の逆元は $${\tau_2}$$
　$${\tau_3}$$ の逆元は $${\tau_3}$$
となり、逆元は $${S_3}$$ に存在します。

　以上によって、$${S_3}$$ は置換の積という演算に関して群となります。ガロアはこの解の置換の集合 $${S_3}$$ には上記の (1)～(4) の構造があることを見出しました。ガロアによる群論の始まりです。そしてそれは「５字以上の方程式に解の公式が存在しない」ことの証明の、核となるアイデアとなります。

　次は『部分集合』、『部分群』、『剰余類』、『正規部分群』と重要な概念を解説し、ガロアの証明のアイデアを紹介して、このシリーズを終える予定です。厳密な証明ではなく、ガロアが何を考えたのかの素朴なアイデアを紹介します。

　最後に、置換の積を計算する上でのコツを述べていきます。結論だけでよければ上記までの内容で完結していますが、実際に計算するときには便利な考え方です。先ほどやった、３次置換を三角形の「回転」と「反転」に見立てる考え方が役立ちます。

置換の積の計算のコツ

(1)　恒等置換の作用があると変化しない。

　恒等置換は、先に作用させても、後に作用させても、相手の置換を変化させません。
例　$${idid=id}$$
　　$${\rho_2id=id\rho_2=\rho_2}$$
　　$${\tau_1id=id\tau_1=\tau_1}$$

(2)　回転同士の積は回転になる。

　回転を表す置換 $${\rho_2,  \rho_3}$$ について
　$${\rho_2}$$ は $${120^\circ}$$ 回転
　$${\rho_3}$$ は $${240^\circ}$$ 回転
を表すので、$${120^\circ}$$ 回転と $${240^\circ}$$ 回転で $${360^\circ}$$ 回転（変化しない）となることから
　$${\rho_2\rho_3=id}$$
　$${\rho_3\rho_2=id}$$
　$${120^\circ}$$ 回転と $${120^\circ}$$ 回転で $${240^\circ}$$ 回転となることから
　$${\rho_2\rho_2=\rho_3}$$
　$${240^\circ}$$ 回転と $${240^\circ}$$ 回転で $${120^\circ}$$ 回転となることから
　$${\rho_3\rho_3=\rho_1}$$
となります。

(3)　反転同士の積は回転になる。

　反転は固定する文字、つまり変化しない文字で覚えて
　$${\alpha}$$ 固定は　$${\tau_1=(\beta     \gamma)}$$
　$${\beta}$$ 固定は　$${\tau_2=(\alpha     \gamma)}$$
　$${\gamma}$$ 固定は　$${\tau_3=(\alpha     \beta)}$$
と覚えます。固定するアルファベット順と、番号の小さい順が対応しています。固定する文字が分かれば、それ以外の文字を入れ替えればよいので簡単です。
　その上で、本シリーズ (16) でやった次の公式を用います。

$$
\begin{align*}
(〇     ♠)(〇     ♣)=(〇     ♠     ♣)
\end{align*}
$$

　つまり$${〇}$$を先頭にして、赤矢印の順に文字を並べていきます。

　この公式から、互換同士の積は３次巡回置換で表されます。つまり反転同士の積は回転になります。

$$
\begin{align*}
\underset{反転}{(〇     ♠)}\underset{反転}{(〇     ♣)}=\underset{回転}{(〇     ♠     ♣)}
\end{align*}
$$

　この公式を使うと互換の積は、次のように３次巡回置換に変換できます。

$$
\begin{alignat*}{2}
\tau_1\tau_2&=(\beta     \gamma)(\alpha     \gamma) & &\\
&=(\underline{\gamma}     \beta)(\underline{\gamma}     \alpha)　& &{\small（共通に含む文字を先頭にする）}\\
&=(\underline{\gamma}     \beta     \alpha) & &{\small（下線部を先頭に公式を使う）}\\
&=(\alpha     \gamma     \beta) & &{\small（\alpha  を先頭に変える）}\\
&=\rho_2
\end{alignat*}
$$

　なお巡回置換は、適切に文字の順を変えて表記すれば、同じ置換となります。
$${\beta \rightarrow \underline{\gamma \rightarrow \beta}}$$ より
　$${(\beta     \gamma)=(\underline{\gamma     \beta})}$$
$${\alpha \rightarrow \underline{\gamma \rightarrow \alpha}}$$ より
　$${(\alpha     \gamma)=(\underline{\gamma     \alpha})}$$
$${\gamma \rightarrow \beta \rightarrow \underline{\alpha \rightarrow \gamma \rightarrow \beta}}$$ より
　$${(\gamma     \beta     \alpha)=(\underline{\alpha     \gamma     \beta})}$$
　どんな場合でも、適切に文字の順を変えることによって、先ほどの公式が使えるようになります。
　もう一つ例を示します。他の場合も同様です。

$$
\begin{alignat*}{2}
\tau_1\tau_3&=(\beta     \gamma)(\alpha     \beta)\\
&=(\underline{\beta}     \gamma)(\underline{\beta}     \alpha)　& &{\small（共通に含む文字を先頭にする）}\\
&=(\underline{\beta}     \gamma     \alpha) & &{\small（下線部を先頭に公式を使う）}\\
&=(\alpha     \beta     \gamma) & &{\small（\alpha  を先頭に変える）}\\
&=\rho_3
\end{alignat*}
$$

$$
\begin{alignat*}{2}
\tau_3\tau_1&=(\alpha     \beta)(\beta     \gamma)\\
&=(\underline{\beta}     \alpha)(\underline{\beta}     \gamma)　& &{\small（共通に含む文字を先頭にする）}\\
&=(\underline{\beta}     \alpha     \gamma) & &{\small（下線部を先頭に公式を使う）}\\
&=(\alpha     \gamma     \beta) & &{\small（\alpha  を先頭に変える）}\\
&=\rho_2
\end{alignat*}
$$

　この例より $${\tau_1\tau_3\ne\tau_3\tau_1}$$ となります。
　$${\rho_2\rho_3=\rho_3\rho_2 (=id)}$$
と等しくなる場合もありますが、置換の順を変えると一般には等しくなりません。
　なお、同じ互換同士の積は、一度反転し、再び同じ反転で元に戻る（変化しない）ので、$${0^\circ}$$ 回転とみなし、恒等置換 $${id}$$ となります。
　$${\tau_1\tau_1=id}$$
　$${\tau_2\tau_2=id}$$
　$${\tau_3\tau_3=id}$$

(4)　回転と反転の積は反転になる。

　このケースは、変化しない文字を見極めます。互換と３次巡回置換の積は互換になる、つまり「回転と反転の積は反転」になるという事実を知った上で、どの文字が変化しないかが分かれば互換で表すことができます。例えば

$$
\rho_2\tau_1=(\alpha     \underline{\gamma     \beta})(\underline{\beta     \gamma})
$$

は、下線部より
　$${\gamma \rightarrow \beta}$$　から　$${\beta \rightarrow \gamma}$$
の入れ替えが入るので、$${\gamma}$$ は
　$${\gamma \rightarrow \beta \rightarrow \gamma}$$
と（一度 $${\beta}$$ を経由してから）元に戻ることが分かり、 $${\gamma}$$ の変化しない反転であることが分かります。よって

$$
\begin{alignat*}{3}
\rho_2\tau_1&=(\alpha     \underline{\gamma     \beta})(\underline{\beta     \gamma})　& &\\
&=(\alpha     \beta) & & {\small (\gamma  が不変の反転)}\\
&=\tau_3
\end{alignat*}
$$

となります。また

$$
\begin{align*}
\rho_2\tau_2=(\alpha     \gamma     \beta)(\alpha     \gamma)
\end{align*}
$$

は

$$
\begin{align*}
\rho_2\tau_2&=(\alpha     \gamma     \beta)(\alpha     \gamma)\\
&=(\underline{\alpha     \gamma}     \beta)\hspace{-4pt}\underset{順を変える}{(\underline{\gamma     \alpha})}
\end{align*}
$$

と、後の互換の文字の順を変えると、下線部より
　$${\alpha \rightarrow \gamma}$$　から　$${\gamma \rightarrow \alpha}$$
の入れ替えが入ると分かるので、$${\alpha}$$ は
　$${\alpha \rightarrow \gamma \rightarrow \alpha}$$
と（一度 $${\gamma}$$ を経由してから）元に戻ることが分かり、$${\alpha}$$ の変化しない反転であることが分かります。よって

$$
\begin{alignat*}{2}
\rho_2\tau_2&=(\alpha     \gamma     \beta)(\alpha     \gamma) & &\\
&=(\underline{\alpha     \gamma}     \beta)(\underline{\gamma     \alpha})　& &{\small (文字の順を変える)}\\
&=(\beta     \gamma) & &{\small (\alpha  が不変の反転)}\\
&=\tau_1 & &
\end{alignat*}
$$

　このように、文字の順を適切に変えることによって、変化しない文字が判断できるようになります。
　$${〇 \rightarrow \triangle}$$　から　$${\triangle \rightarrow 〇}$$
と文字が入れ替わると、それは $${〇}$$ が不変の反転です。
　もう１つ例を与えます。

$$
\begin{alignat*}{3}
\rho_2\tau_3&=(\alpha     \gamma     \beta)(\alpha     \beta) & &\\
&=(\underline{\beta     \alpha}     \gamma)(\underline{\alpha     \beta})　& &{\small (文字の順を変える)}\\
&=(\alpha     \gamma) & &{\small (\beta  が不変の反転)}\\
&=\tau_2 & &
\end{alignat*}
$$

　この場合、初めの３次巡回置換の文字を入れ替えると分かりやすくなります。互換の方の順を変えるか、３次巡回置換の方の順を変えるかは、臨機応変に対応します。
　では、上の３つに続いて、先に $${\rho_1,  \rho_2}$$、後に $${\tau_1,  \tau_2.  \tau_3}$$ のすべての組み合わせを計算していきます。

$$
\begin{alignat*}{3}
\rho_3\tau_1&=(\alpha     \beta     \gamma)(\beta     \gamma) & &\\
&=(\alpha     \underline{\beta     \gamma})(\underline{\gamma     \beta})　& &{\small (文字の順を変える)}\\
&=(\alpha     \gamma) & &{\small (\beta  が不変の反転)}\\
&=\tau_2 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\rho_3\tau_2&=(\alpha     \beta     \gamma)(\alpha     \gamma) & &\\
&=(\underline{\gamma     \alpha}     \beta)(\underline{\alpha     \gamma})　& &{\small (文字の順を変える)}\\
&=(\alpha     \gamma)　& &{\small (\gamma  が不変の反転)}\\
&=\tau_3 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\rho_3\tau_3&=(\alpha     \beta     \gamma)(\alpha     \beta) & &\\
&=(\gamma     \underline{\alpha     \beta})(\underline{\beta     \alpha})　& &{\small (文字の順を変える)}\\
&=(\beta     \gamma)　& &{\small (\alpha  が不変の反転)}\\
&=\tau_1 & &
\end{alignat*}
$$

　先に互換、後に３次巡回置換のときも、同様に互換となります。
先に $${\tau_1,  \tau_2.  \tau_3}$$、後に $${\rho_1,  \rho_2}$$ のすべての組み合わせを計算していきます。

$$
\begin{alignat*}{3}
\tau_1\rho_2&=(\underline{\beta     \gamma})(\alpha     \underline{\gamma     \beta}) & &\\
&=(\alpha     \gamma)　&　&{\small (\beta  が不変の反転)}\\
&=\tau_2 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\tau_1\rho_3&=(\beta     \gamma)(\alpha     \beta     \gamma) & &\\
&=(\underline{\gamma     \beta})(\alpha     \underline{\beta     \gamma}) &　&{\small (文字の順を変える)}\\
&=(\alpha     \beta)　&　&{\small (\gamma  が不変の反転)}\\
&=\tau_3 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\tau_2\rho_2&=(\alpha     \gamma)(\alpha     \gamma     \beta) & &\\
&=(\underline{\gamma     \alpha})(\underline{\alpha     \gamma}     \beta) &　&{\small (文字の順を変える)}\\
&=(\alpha     \beta)　&　&{\small (\gamma  が不変の反転)}\\
&=\tau_3 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\tau_2\rho_3&=(\alpha     \gamma)(\alpha     \beta     \gamma) & &\\
&=(\underline{\alpha     \gamma})(\underline{\gamma     \alpha}     \beta) &　&{\small (文字の順を変える)}\\
&=(\beta     \gamma)　&　&{\small (\alpha  が不変の反転)}\\
&=\tau_1 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\tau_3\rho_2&=(\alpha     \beta)(\alpha     \gamma     \beta) & &\\
&=(\underline{\alpha     \beta})(\underline{\beta     \alpha}     \gamma) &　&{\small (文字の順を変える)}\\
&=(\beta     \gamma)　&　&{\small (\alpha  が不変の反転)}\\
&=\tau_1 & &
\end{alignat*}
$$

$$
\begin{alignat*}{3}
\tau_3\rho_3&=(\alpha     \beta)(\alpha     \beta     \gamma) & &\\
&=(\underline{\beta     \alpha})(\underline{\alpha     \beta}     \gamma) &　&{\small (文字の順を変える)}\\
&=(\alpha     \gamma)　&　&{\small (\beta  が不変の反転)}\\
&=\tau_2 & &
\end{alignat*}
$$

　以上、(1)～(4) を押さえておけば、どのような置換の積でも簡単に計算できます。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く