
勉強コラム 統計学編 3. 2変量のデータ
※このノートは私が分かりやすい表現で記載してます。厳密な定義は教科書を参照してください。今回は特に私の独特なイメージによる表現が強いです。
前回までは1変量のデータの解析に関して、偏差や分散、標準偏差について勉強しました。
今回は統計学の第3弾として2変量のデータについて勉強します。2つの変量に対して相関係数や回帰直線の求め方について取り扱います。今回は2変量のデータなので前回までの例題データに新しい変量yのデータを足して、勉強していきます。
まず、例題としてあるクラスの英語および数学のテストの点が以下のような結果であったとする。このようなデータでは、数学の点数と英語の点数という2つのデータの種類が存在している。数学の点数のデータを変量x、英語の点数のデータを変量yとする。

1.散布図
散布図とは、2つの変量xおよびyを平面座標系にプロットしたグラフのことである。今回の場合、横軸を数学の点数、縦軸を英語の点数としてこれらのデータをプロットする。Excelでは挿入タブのグラフの中に散布図というツールがあり、以下のようなグラフを描画できる。
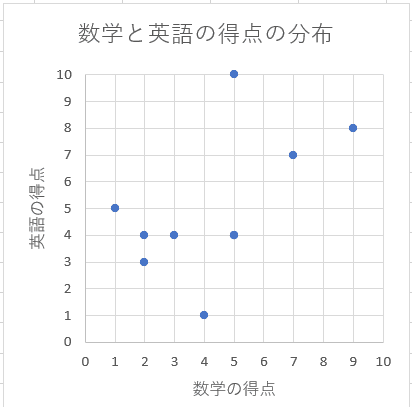
(変量の単位系が同一の場合、縦軸と横軸のスケール(描画範囲)をそろえるほうが見やすい。)
散布図を作成することにより、2つの変量の関係性が一目で理解することができる。なお、2変量の場合でもデータの大きさに関しては各変量のデータの大きさ(基本的にはそろっている前提)と同じである。今回の例題では、データの大きさは英語の点数というデータが増えても、各変量に10個のデータが存在するので、大きさは「10」となる。
また、表1のようなデータの場合、以下のような棒グラフでデータを表現することもできる。
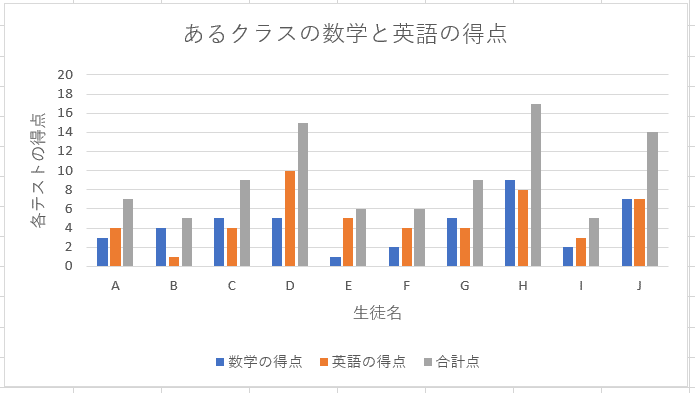
図1のような散布図は、横軸を数学、縦軸を英語の点数としているので、あるクラスに在籍する生徒の数学と英語の点数の関係性について表現することができる。一方、図2のような棒グラフは、横軸を生徒、縦軸をそれぞれのテストの点数としているので、生徒の順位やテスト成績、生徒間の習熟度の差を表現することができる。このように、グラフは表現したい内容によって、縦軸と横軸の取り方を変える必要があることに留意しなければならない。
2.2変量のデータの解析
1変量の場合、データの解析のパラメータとして、偏差や分散、標準偏差といったものがある。おさらいすると、
①平均値:データの数値の総和をデータの大きさで割った値
②中央値:データを小さいほうから並べたときに中央となる値
③最頻値:度数分布で最も度数が高い階級の階級値(最もデータが多く存在するデータ区間の中央値)
④偏差:平均値に対するデータの各数値の差分
⑤分散:偏差の2乗和の平均値。データの平均値に対する各データの差分の2乗和平均。データのばらつきの大きさを定性的に表せる。(値が大きい→ばらつきが大きい、値が小さい→ばらつきが小さい。どのくらいのばらつきかはわからない。)
⑥標準偏差:分散の平方根。データの平均値に対するデータの差分の平均値。データのばらつきの大きさを定量的に表せる。(値が大きい→ばらつきが大きい、値が小さい→ばらつきが小さい。その数値からばらつきの平均値が大体把握できる。)
(一般化した数式は前回の記事を参照してください。)
2変量であっても、それぞれに上記の解析を行い、データをそれぞれのパラメータで表現することはもちろんできる。今回は、2変量のデータの解析ということで、2変量間の関係性を表現できるパラメータに関してまとめる。
まず、データの大きさがnである2変量のデータは、以下のように表される。
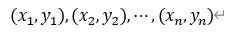
2.1.共分散
共分散とはxおよびyの変量の偏差(データから平均値を引いた値)の積の平均値のことである。数式で表現すると、
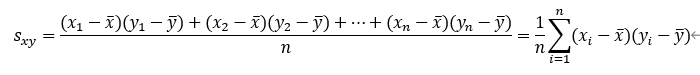
となる。共分散は数値ごとの場合分けから意味合いを紐解くと以下のような解釈ができる。
・共分散が大きい(0から離れている)→xの偏差とyの偏差が大きいことから、xが平均値から離れると、yも平均値から離れる。つまり、xが変化するとyも同様な変化をする。
・共分散が小さい(0に近い)→xまたはyのどちらかの偏差が大きくても、もう一方が小さいことから、xが平均値から離れても、yは平均値から離れない、またはその逆が起こる。つまり、xが変化しても、yはxと同様な変化はしない。
・共分散が正の値:xがプラス偏差の場合、yもプラス偏差である。つまり、xとyが正の比例関係のようにxが増加するとyも増加するような関係性にあるということ。
・共分散が負の値:xがプラス偏差の場合、yはマイナス偏差になる。つまりxとyが負の比例関係のようにxが増加するとyは減少するような関係性にあるということ。
文章にして書くと解釈が非常にややこしいので、絵にかいて表現してみる。

図3は偏差の正負の関係性を散布図上に図示したグラフである。偏差は各データの数値から平均値を引いた値であるため、XおよびYの平均値の線を中心軸として考えた場合の第1象限と第3象限に相当するエリアにプロットされたデータはXとYの偏差の積が正の値になる(プラス×プラスまたはマイナス×マイナス)。逆に第2象限および第4象限に相当するエリアにプロットされたデータはXとYの偏差の積が負の値になる(マイナス×プラスまたはプラス×マイナス)。したがって、
Case1「共分散が正の値である場合」:
プロット全体がXとYの平均線を中心軸としてみた場合の第1象限と第3象限のエリアに偏っていることが推測できる。
Case2「共分散が負の値である場合」:
プロット全体がXとYの平均線を中心軸としてみた場合の第2象限と第4象限のエリアに偏っていることが推測できる。
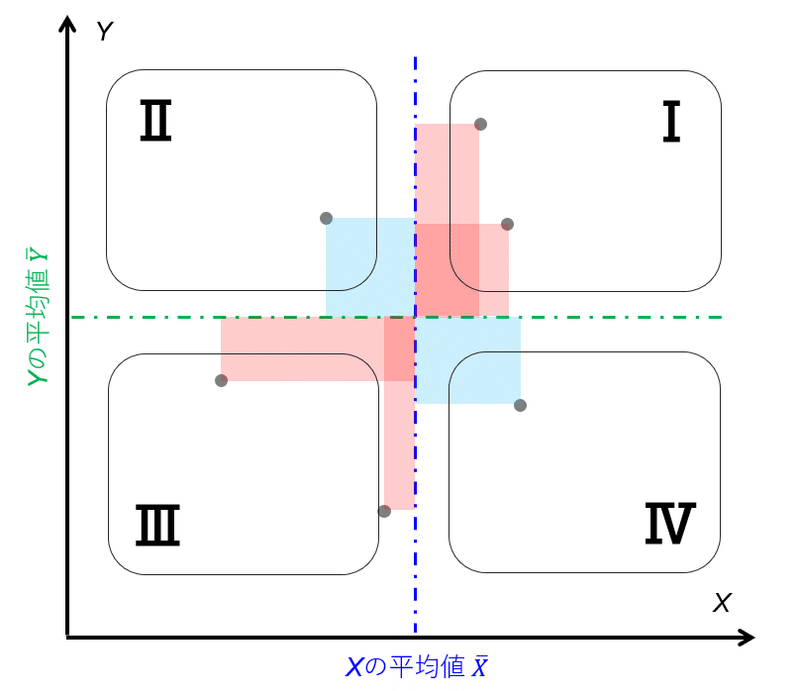
図4は偏差の大きさを散布図上に図示したグラフである。図4中のXおよびYの平均値とプロットによって囲まれた面積(図中の赤枠および青枠)が各プロットにおけるXとYの偏差の積に相当する。よって、共分散はその面積の平均値に相当するということになる。したがって、
Case3「共分散の絶対値が小さい場合」:
プロット全体がXとYの平均線を中心軸としてみた場合のその中心点付近にプロットが偏っている、あるいはその中心点から放射状に均一に分布していることが推測できる。
Case4「共分散の絶対値が大きい場合」:
プロット全体が、XとYの平均線を中心軸としてみた場合の中心点から遠い位置に分布している、かつ第1象限および第3象限または第2象限および第4象限のエリアどちらかに偏っていることが推測できる。
なお、共分散には1変量の分散と同じように各変量の平均値を用いて簡単に算出できる。
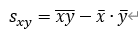
xをyと置き換えれば1変量の分散の関係式になる。証明は1変量と同様に求めることができる。
2.2.相関係数
相関係数とは、共分散を各変量X、Yの標準偏差SxおよびSyの積で割った値である。数式で表現すると以下のようになる。
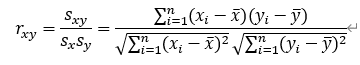
相関係数は、XおよびYの標準偏差の積に対する共分散の割合である。つまり、データの平均値に対する各平均値の差分の平均を基準として、XとYの分布を表現している。
このままでは相関係数がどのようなパラメータか理解しづらいので、図を使って説明する。(あくまで私の独特のイメージなので、人によってはわかりずらいと思います笑。)
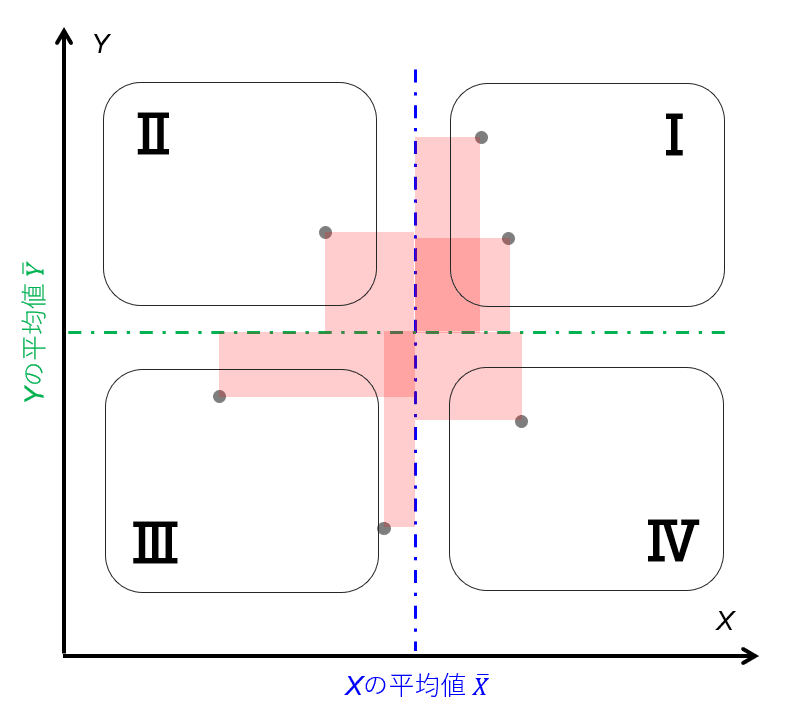
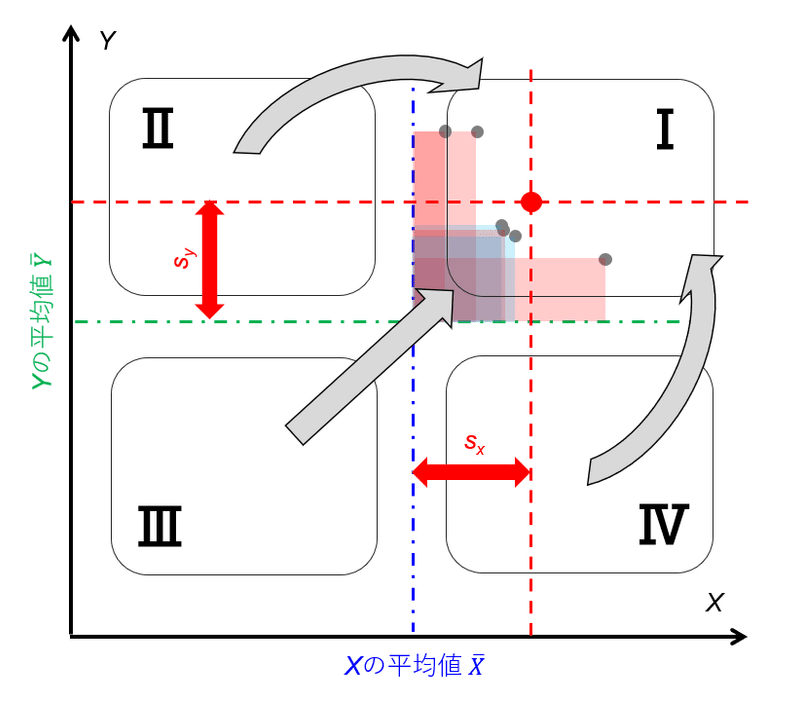
図4のように散布図の中心軸をXとYの平均値とする。変量Xおよび変量Yの標準偏差SxおよびSyは、もともとの意味合いを考えると、「X(Y)の平均値との差分の絶対値の平均値」である(厳密には違うがこのように考えると自分的にわかりやすい。)から、言い換えると「平均からどれぐらい離れているかの距離(方角は考えない)の平均値」ともいえる。そのような標準偏差の積であるため、図3の面積の考え方を元にすると、図4のような面積に関して正負を考えない場合の面積の平均値といえる(図5)。ある意味でいえば、次の図6のようにXとYの平均値を中心軸とした場合に、第2から第4象限のプロットを第1象限にミラーリング(軸対象移動または点対象移動)し、その時の面積の平均値というイメージをすることができる。
相関係数についてまとめると、
・相関係数は図4に示した面積の平均値と図5に示した面積の平均値の比である。工学的に言うなら、XとYの面積という同種の物理量の比であるから無次元数であるといえる。
・分子(共分散)と分母(標準偏差の積)の違いは、その面積の正負を考慮するかどうか。理由は共分散はXとYの偏差の積の平均値であるため偏差は正負どちらの数値にもなるが、標準偏差は偏差の2乗の平均の平方根、つまり偏差が負でも2乗して平方根をとるので必ず正の数値になる。したがって標準偏差の積も必ず正の値になる。
このことから、相関係数はその数値から図7から図9のような散布図を推定することができるパラメータであることがわかる。
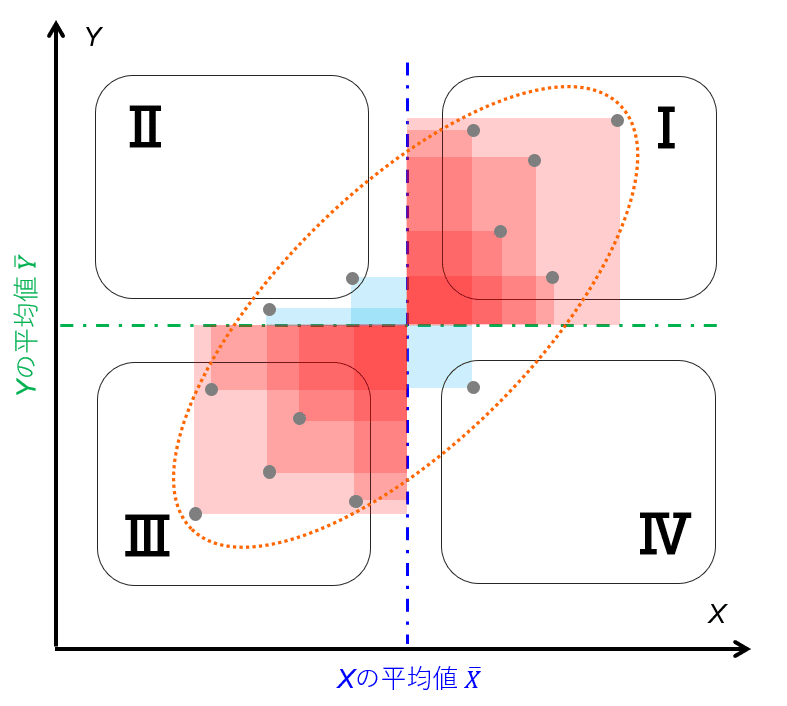
(1に近いと第1象限と第3象限にプロット全体が偏っていることが推定できる。)
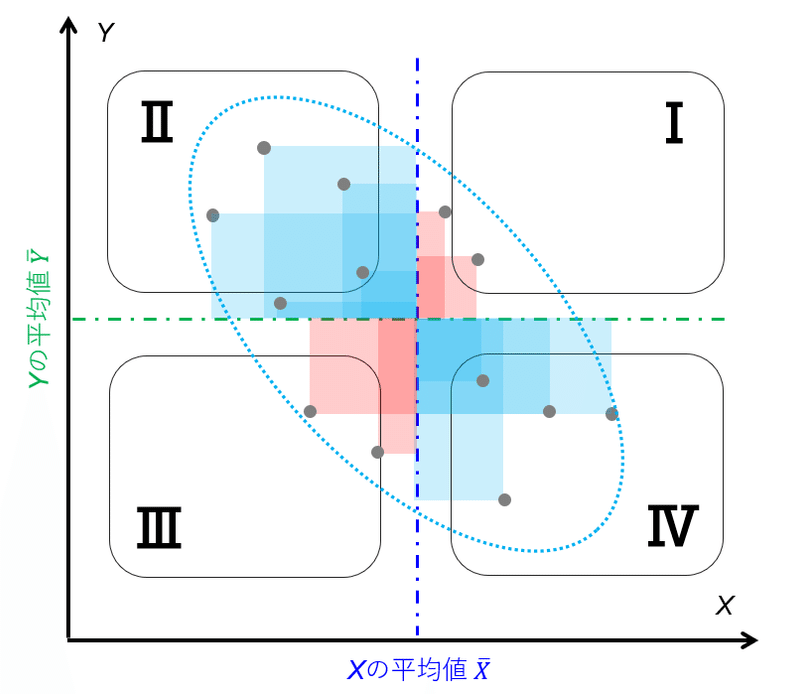
(‐1に近いと第2象限と第4象限にプロット全体が偏っていることが推定できる。)
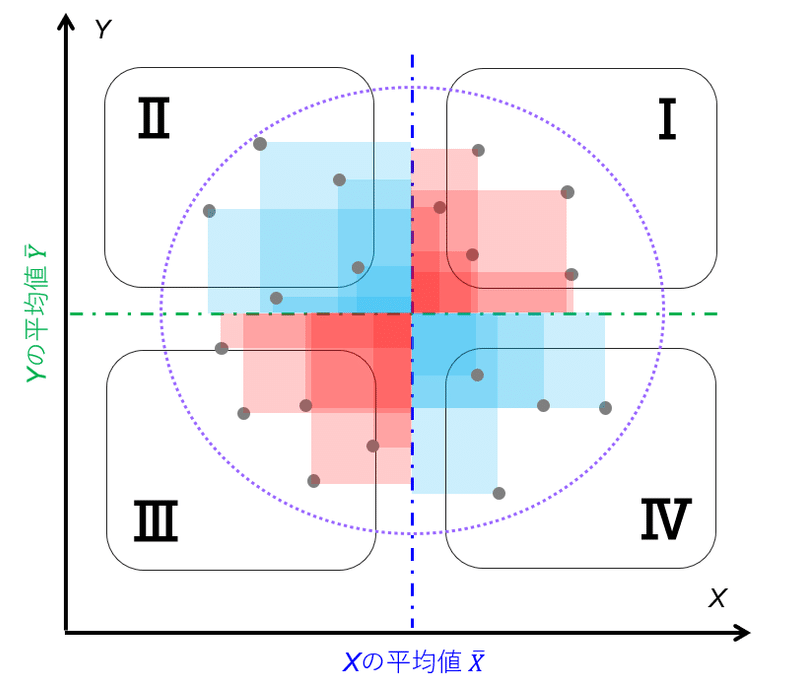
(0に近いと第1象限から第4象限にプロット全体満遍なく分布していることが推定できる。)
なお、変量X、Yに対して変量Z、Wが、

の関係が成り立つ場合、その変量Z、Wの相関係数rzwは、以下の関係が成り立つ。
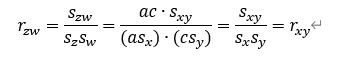
3.回帰直線
回帰直線とは、ある2変量X、Yの関係をある1本の直線で表そうとしたときのその直線のことである。回帰直線は現在あるデータの分布に基づいて、これから取得する変量Xのデータから変量Yを予測するためのものである。
回帰直線としているので直線の式を用いる。変量XおよびYについて以下の関係式が成り立つとする。
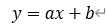
この時、変量Yは変量Xによって説明できる。この場合、Xを説明変数、Yを目的変数、または、Xを独立変数、Yを従属変数と呼ぶ場合がある。
傾きa、切片bの直線の関係が成り立つ場合、あるデータ(xi, yi)に対して
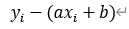
を誤差と呼ぶ。yiは実際のデータの数値であるのに対して、axi+bはxiというデータから回帰直線y=ax+bを用いて求めたyiの予測値であるため、その差分が実際のデータと予測値との誤差となる。
この誤差の平方和(2乗和)が最小となるようにaとbの数値を決定すれば、y=ax+bがそれらのプロット全体に対して真ん中を通る直線(平均的な直線)となる。(二乗和の最小をとるこの手法を最小二乗法という。2つの変数の関係性がもともとわかっている場合(線形なのか、指数関数なのか、、、)に使用することができる。)誤差を2乗にしているのは、偏差の時と同様で、正負の方向がある誤差を単純に足すとゼロになってしまうからである。2乗すれば、すべての誤差が正の実数となり、積算してもゼロにならない。
誤差 yi-(ai+b) の2乗和を変数aおよびbの2変数関数だと考えて、
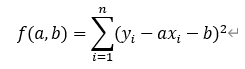
とすると、aおよびbの偏微分の導関数がそれぞれ0になるとき、a,bは極値となる。
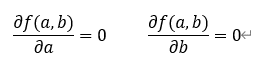
これを計算していくと、aおよびbは、
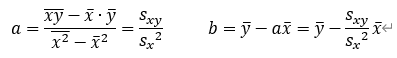
となり、回帰直線y=ax+bは以下の式になる。
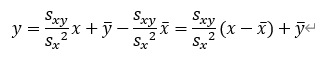
なお、2.2.の相関係数rxyを用いて表現しなおすと、aは
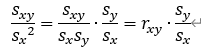
となるから、回帰直線は以下の式になる。(この式もまた回帰直線の本質を表しているように思います。また下の式は形として非常に覚えやすいです。)
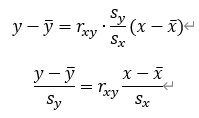
この式を言葉で解釈すると回帰直線は「XおよびYの平均値を中心軸とし(XおよびYの平均値を通り)、XおよびYの誤差の平均値の比に相関係数によるデータの散らばり具合の補正を考慮した勾配によって引くことのできる直線」となる。「相関係数による補正」と表現したのは、標準偏差が正負の情報を持っていないため、つまり方角の情報を持っていないためである。また下の式で表現すると、「XとYのデータを標準化し、傾きを相関係数とした直線」ともいえる。(データの標準化については前回のコラムで勉強しました。)
図で表現すると以下のようになる。
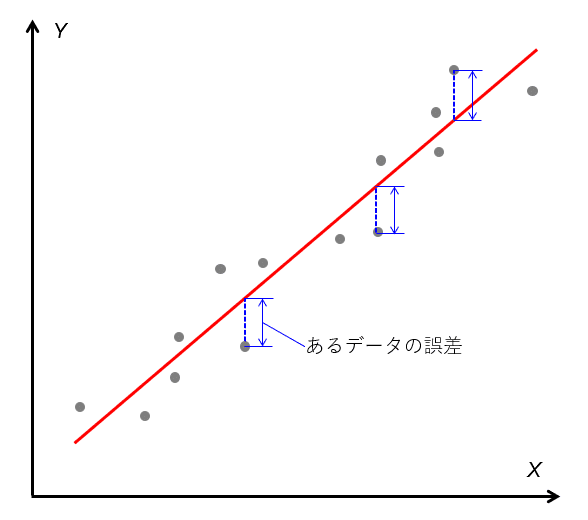
(データすべての誤差の二乗和が最小となるような勾配(Slope)、切片(Intercept)を持つ直線)
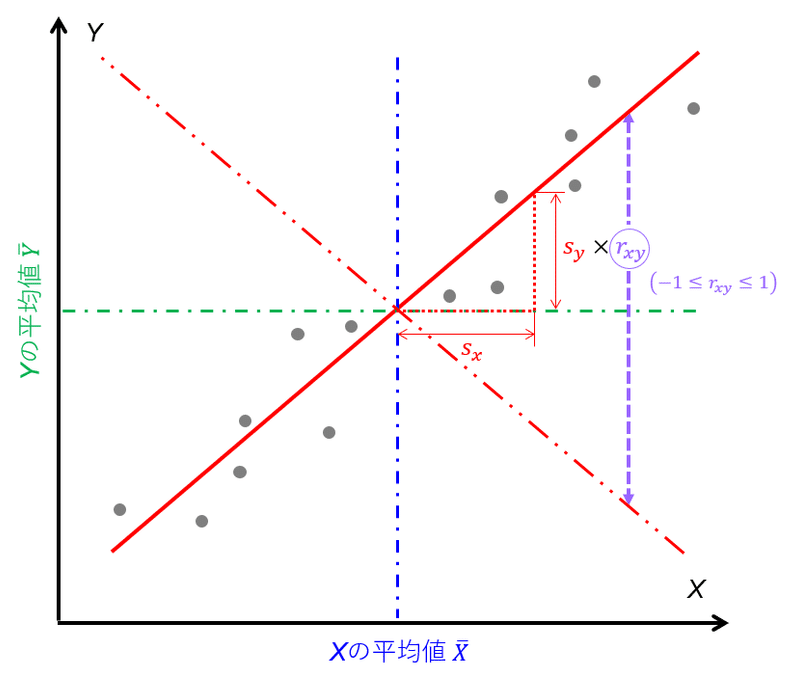
(XとYの平均値を中心として、XとYの標準偏差の勾配に相関係数による補正を考慮した直線)
4.まとめ
今回は2変量のデータの解析について勉強しました。まとめると、
①散布図:2つの変量を縦軸、横軸にしデータをプロットしたグラフのこと
②共分散:xおよびyの変量の偏差(データから平均値を引いた値)の積の平均値。図4に示す面積の平均値。符号と数値の大きさからどのような分布のデータかある程度推定できる。
③相関係数:XおよびYそれぞれの標準偏差に対する共分散の比。図5に示した面積の絶対値の平均値に対する図4に示した面積の平均値の比。回帰直線の式から考えると、プロット全体に対して、XとYを標準化した変量VおよびWの比(W/V)ともいえる。
④回帰直線:2変量X、Yのデータに対して直線関係がある多考えた場合のその直線式のこと。その式は、すべてのプロットとの誤差の二乗和が最小となるような勾配(Slope)と切片(Intercept)を持つ直線である。言い換えると、XとYの平均値を中心軸とし、YとXの標準偏差の比による勾配に相関係数による補正を考慮した直線のこと。
大変長くなりましたが、以上になります。ご精読ありがとうございました。相関係数や回帰直線をイメージとして理解するのに、長くなってしまいました笑。文章としても、時間的にも。
次回はいったんこれまでの内容の理解を促進するために、何かのデータに関して演習をやりたいと思います。
もしよろしければ、スキ、コメント、フォローよろしくお願いします。本記事が誰かの役立てれば光栄です。
この記事が気に入ったらサポートをしてみませんか?
