※このノートは私が分かりやすい表現で記載してます。厳密な定義は教科書を参照してください。

　今回は統計学の第2弾として1変量のデータ解析について勉強します。分散や偏差などデータを比較、検討するためのデータの処理についてです。ちなみに、高校数学の学習指導要領を確認してみたら、2012年あたりからデータの分析でこのあたりの内容を勉強するようになっていたんですね。。。
　今回は前回と同様の例題データを用いてそのデータの解析について勉強していきます。

1．代表値

　代表値とは、データの特徴を捉えることができる数値のことである。以下の3つが一般的によく知られている。

1．1．平均値

　（データの総和）÷（データの大きさ（データの総個数））で表される数値のことである。単に平均とも呼ばれる。表1のデータの平均は、(3+4+5+5+1+2+5+9+2+7) / 10 = 4.3となる。なお、ExcelではAVERAGE関数で算出できる。

1．2．中央値（メジアン）

　データを小さい順に並べたときに、真ん中に位置する数値のことである。データの大きさが奇数の場合は真ん中の数値は1つに決まるが、偶数の場合は中央の数値が2つになる。その場合はその2つの数値の平均値を中央値とする。表1のデータの中央値は、5番目の4点と6番目の5点の平均値をとって、4.5となる。なお、ExcelではMEDIAN関数で算出することができる。

1．3．最頻値（モード）

　度数分布表で度数が最大の階級の階級値のことである。統計学編1．の度数分布表から、度数が最大の階級は「4点以上、6点未満」の階級でその階級値は5であるから、最頻値は5になる。階級の区間を変更すれば当然階級値も異なってくる。なお、ExcelではMODE関数で算出することができる。

2．ばらつきの指標

　代表値では、そのデータのヒストグラムの形を推測することはできない。その場合はデータのばらつき具合を示す指標を用いることで推測することができる。

2．1．偏差

　データの各数値から平均値を引いた値のことである。偏差の総和は必ず0になる。

2．2．分散

　各データの偏差の平方和（偏差の2乗の総和）をデータの大きさで割った値のことである。つまり、偏差の2乗の平均値のことである。もっとざっくりいうと「平均値に対する差分の2乗の平均値」と表現できる。分散が大きいということはヒストグラムの形が幅の広い山形であることが推測できる。逆に分散が小さければ、平均値付近にデータが密集していることが推測できる。つまり、データの散らばり具合を定性的に表現できるパラメータということができる。（分散の数値から平均値を基準としてどの程度ばらついているかは数値として明確にならないが、ばらつきが大きいのか？小さいのか？ということはわかる。）

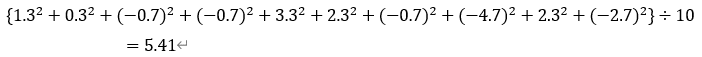
2．3．標準偏差

　分散の平方根をとった値のことである。Excelでは、STDEV関数で算出することができる（英語でstabdard deviationという。よく出てくる表現。）。式から意味合いを読み解くと、標準偏差は平均値に対する各データの差分の2乗和平均の平方根ということになる。もっとざっくり表現すると、「平均値に対する差分の平均値」といえる。つまり、データの散らばり具合を定量的に表現できるパラメータということができる。（標準の数値から平均値を基準としてばらつきの平均値がどの程度か明確になっている。）

3．各解析の数式による表現（一般化した表現）

　次に、2．、3．で述べた解析値について数式で一般化した表現にする。
　まず、n個からなるあるデータがx1, x2, x3, … , xnと表されるとすると、
・データの大きさ（データの総個数）：n
・データの各数値：x1, x2, x3, … , xn
・データの平均（エックスバー）：

・偏差（データの各数値から平均を引いたもの）：

　なお偏差の総和は、以下の式により0になることがわかる。

・分散（偏差の2乗和平均、Sx^2で表される）：

・標準偏差（偏差の2乗和平均の平方根、Sxで表現される）：

となります。なお、以上の式より平均値と2乗平均値、分散には以下の関係式が成り立ちます。

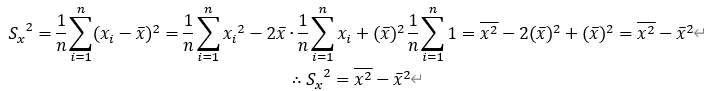
また、分散の基準値を平均ではなく別の値を用いる場合、上式の関係式から簡単に計算しなおすことができる。分散の基準値をある真値aにして計算する場合、xiをxi-aに置き換えることで求まる。（平均値を間違えた場合や後から平均値が変化した場合に役立つ。）

4．変量の変換

　世の中の計測機器は様々な単位系で計測値を表示するものがある。単位系の変換にはその単位系の変換式を使用して変換することができる。今回はy=ax+bという関係が成り立つ場合に変量xを変量yに変換したときのそれぞれの解析値について考える。y=ax+bの関係が成り立つ変量x, yは様々あり、例えば「勉強コラム　熱力学編 1.」で勉強した熱の仕事当量（kcalからkJへの変換）や、摂氏温度、華氏温度、および絶対温度もy=ax+bの関係性を持つ。

　ある変量xに対してy=ax+bという関係を持つ変量yについて、yの平均値、分散標準偏差は以下が成り立つ。

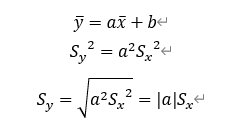
5．データ量の標準化

　あるデータをほかのデータと相対評価する場合、データ量を標準化することが重要になる。例えば、高校生がある模試を受けた場合に、前回から今回で得点自体はアップしたが、全国順位は下がったというケースがあったりする。このような場合は、単純に平均値が上がっている（みんなもいい点が取れた場合）場合や点差が人によって大きく開き、平均点はたいして変化しなくても上位陣が大きく点数を伸ばした（標準偏差が大きくなった）場合がある。このような時系列上での自分のデータの比較だけでなく、順位のような他のデータとの相対比較の場合は、単純にデータの偏差を見るだけでなく、標準化して見比べる必要がある。（順位を見る場合は偏差の基準値を平均値ではなく中央値にしたほうがわかりやすい。）
　データの標準化にはあるデータxの平均値と標準偏差を持ちいて新しい変量yを作成する。

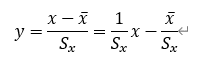
この関係式の意味を考えてみると、「標準偏差に対する偏差の割合」、言い換えると「平均値に対する差分の平均値に対してこのデータの平均値に対する差分の割合」ということになる。この値で見ると、データx自体が上昇した（テストの点数が上昇した）場合でも、平均値（受験生全体の平均得点）や標準偏差（受験生全体の得点の平均点に対する差分の平均点）によっては変量yは上がらない場合もある。
　このように、データを比較する場合は、標準化（規格化）しないと自分が欲する情報に対する正確な回答が読み取れない場合がある。

6．まとめ

　今回は変量の解析について勉強しました。まとめると、
①平均値：データの数値の総和をデータの大きさで割った値
②中央値：データを小さいほうから並べたときに中央となる値
③最頻値：度数分布で最も度数が高い階級の階級値（最もデータが多く存在するデータ区間の中央値）
④偏差：平均値に対するデータの各数値の差分
⑤分散：偏差の2乗和の平均値。データの平均値に対する各データの差分の2乗和平均。データのばらつきの大きさを定性的に表せる。（値が大きい→ばらつきが大きい、値が小さい→ばらつきが小さい。どのくらいのばらつきかはわからない。）
⑥標準偏差：分散の平方根。データの平均値に対するデータの差分の平均値。データのばらつきの大きさを定量的に表せる。（値が大きい→ばらつきが大きい、値が小さい→ばらつきが小さい。その数値からばらつきの平均値が大体把握できる。）
⑦各種解析では基準値をデータの平均としているが、基準値を平均して解析することも可能（中央値や、最頻値、50としたりして偏差、分散、標準偏差を計算しなおすことができる。）
⑧データを相対比較する場合は、そのデータの数値の差分や偏差だけでなく、標準化した値も見る必要がある。標準化は、標準偏差に対する偏差の割合。

　今回は以上になります。データ解析の基礎となるパラメータが多数登場しました。次回は、2変量のデータに関して勉強していこうと思います。
　ご精読ありがとうございました。もしよろしければ、スキ、コメント、フォローよろしくお願いします。