キーワード

• 高次元ホモトピー群

• ホモトピー

• 可換性

該当箇所

高次元ホモトピー群は常に可換である（中略）この主張を確かめるには図4.18を注意深く観察すると良い。明らかに、これらの変形は各ステップでホモトピックである。

解説

$${\alpha, \beta}$$の境界を基点$${x_0}$$へと潰すので、$${\alpha, \beta}$$を収縮させるなどせずともホモトピーを構成することができる。直観的には下の図のようにすれば良い。

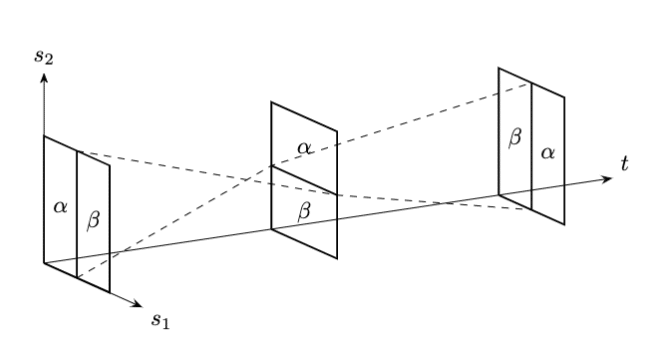
1次元ホモトピー群にはこれに該当する操作が存在しない。

実際にホモトピーを式で書き上げるとなればテキスト図4.18の方が簡単だろう。その際は図4.18の塗りつぶされた部分を全て基点$${x_0}$$に飛ばせば良い。すなわち

$$
F(s_1,s_2,t)=\begin{cases}\begin{cases}F(s_1,\frac{s_2}{1-2t},0)&(s_1≤1/2, s_2≤1-2t)\\F(s_1, \frac{s_2-2t}{1-2t}, 0)&(s_1≥1/2, s_2≥2t)\\x_0&(\mathrm{otherwise})\end{cases}&(t<1/3)\\\begin{cases}F(s_1-\frac{3}{2}(t-1/3), 3s_2, 0)&(s_2≤1/3, \frac{3t-1}{2}≤s_1≤\frac{3t}{2})\\F(s_1+\frac{3}{2}(t-1/3), 3s_2-2, 0)&(s_2≥2/3, 1-3t/2≤s_1≤\frac{3(1-t)}{2})\\x_0&(\mathrm{otherwise})\end{cases}&(1/3≤t≤2/3)\\\begin{cases}F(s_1-1/2, (7-6t)s_2, 0)&(s_1≥1/2, s_2≤2t-1)\\F(s_1+1/2, s_2-6(s_2-1)(t-1),0)&(s_1≤1/2, s_2≥2(1-t)\\x_0&(\mathrm{otherwise})\end{cases}&(t>2/3)\end{cases}
$$

とすれば$${t}$$に応じて図のように変化する。