pdf版はこちらから。誤植、質問等は遠慮なくコメントにお願いします。

前提知識

本記事では

• 等角写像を用いた 2 次元静電場決定問題の解法の原理

• 複素積分

• 軌跡

についての知識を前提とします。
等角写像法については、「等角写像の実部・虚部がコーシー・リーマンの関係式からラプラス方程式の解となることを利用して、電位のラプラス方程式の解を求める」という程度の理解があれば問題ありません。

等角写像を探す方針

2つの複素平面の役割

2 次元の静電場を求める際に等角写像を用いる方法があります。等角写像 (複素正則関数) $${f : z \mapsto w}$$ によって、「位置 $${z}$$ での電位は $${φ(z) = \mathrm{Re}\: w}$$ (または $${\mathrm{Im} \:w}$$) である」とできれば、あとは勾配を計算して電場を求めるだけですね。
しかし、境界における電位を的確に反映する等角写像 $${f}$$ を探すのは至難の業です。これを定式化できるのであれば、プロトコルとして定式化し、汎用性を高くしたいところ。その定式化の方針を立てていきましょう。

まず $${z}$$ 平面は物体の配置・形状を表すための平面です。$${z = x + iy}$$ を使って電位 $${φ(x, y)}$$ を求めることを考えれば、この意味を理解するのは難しくないでしょう。
したがって、$${z}$$ 平面ではじめに考える曲線は、境界条件を与える物体 (基本的に導体) の形状に沿うものになります。例えば半径 $${r}$$ の導体球が存在するなら、まず $${|z − c| = r}$$ の曲線上で等電位であることを議論します。

他方、$${w}$$ 平面は電位を表すための平面です。コーシー・リーマンの関係式の要求から、$${w}$$ は実部か虚部かが電位を表します。電場の決定問題で等角写像を使う理由がコーシー・リーマンの関係式にあるため、そりゃそうだろって感じですが。今回は図の描きやすさと参考文献 [1] での使い方から、虚部が電位を表すように、すなわち $${φ(z) = \mathrm{Im} w}$$ となるように統一します。

導体表面上における等角写像の挙動

さて、特に導体表面上では電位が一定なので、$${z}$$ が導体表面を動くとき $${w}$$ の虚部は変わりません。$${z}$$ の動きに対して $${w}$$ が連続に応答する (ジャンプしない) という妥当な要求をすれば、$${z}$$ が電位 $${\phi}$$ の導体表面を動く間、$${w}$$ は実軸に平行な直線 $${\mathrm{Im}\:w=\phi}$$ の上を左右にのみ動きます。

ではこの「$${z}$$ が電位 $${\phi}$$ の導体表面を動く」というのをどのように表現すればいいでしょうか？
高校数学で散々お世話になった軌跡とパラメーターで表すことができます。
結局のところ、導体系の静電場決定問題で使う等角写像は、パラメーターを使った軌跡の問題に帰着することができます。複素平面 $${z}$$ と複素平面 $${w}$$ を繋ぐために一見するとわかりにくいかもしれませんが、根本の考え方は高校数学と大差ありません。

パラメーター $${t\in\mathbb{R}}$$ を使うことで、導体表面は複素平面上の曲線 $${z(t)=x(t)+iy(t)}$$ で表され、その時の電位は $${\phi(t)=\mathrm{Im}\:w(t)}$$ となります。$${z}$$ と $${w}$$ が $${t}$$ の関数で表せたら、あとは「導体表面に対応する点では $${t\in\mathbb{R}}$$ が存在する」という条件からパラメーター $${t}$$ を消去し、導体表面での電位を虚部で与える軌跡 $${w=g(z)}$$ が求まりますね。電位 $${\phi(z)=\mathrm{Im}\:w=\mathrm{Im}\:g(z)}$$ は境界条件をみたし、軌跡 $${g}$$ が正則関数ならコーシー・リーマンの関係式から $${\triangle\mathrm{Im}\:g=0}$$ となります。この $${g}$$ こそ冒頭で求めていた等角写像に他なりません。

パラメーターに関する注意

ここで $${t}$$ というパラメーターはあくまで導体表面をなぞる曲線のためだけにおいたものでした。我々が求めたいのは導体表面に限らず平面内の点で電位を表せるような等角写像です。その性質として「$${z}$$ が2次元領域を動くと $${w}$$ は複素平面上を動く」ことが要求されます。
この理由により、パラメーターには複素数 $${\zeta}$$ を使いましょう。

これで一番大枠の方針は掴めましたが、この説明だけでは等角写像の問題をパラメーター付きの軌跡の問題として解くことは難しいはずです。
いざパラメーター $${\zeta}$$ を使ったところで、$${z(\zeta)}$$ や $${w(\zeta)}$$ の関数形は想像もつかないでしょう。また作り方によっては関数が開領域で正則になるか (等角写像になるか) も非自明です。
巨人の肩に乗りましょう。

シュワルツ・クリストッフェル変換

ここで登場するのが Schwarz-Christoffel 変換を用いた方法です。

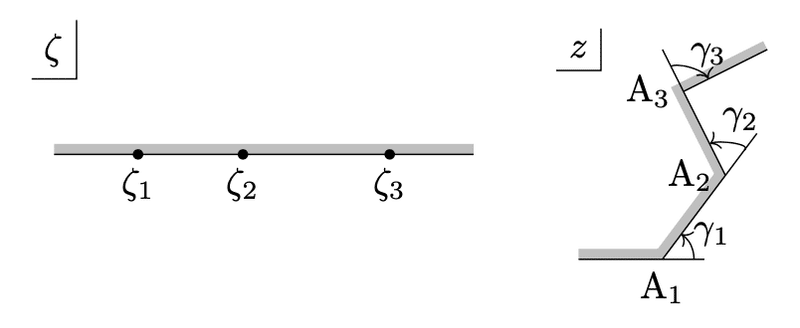
シュワルツ・クリストッフェル変換の境界線における挙動のイメージ

一般的な描像は図に示す通りです。ここでは証明に深入りせず、境界に関するイメージをつかむ程度にしましょう。

$${\zeta}$$ を $${-\infty}$$ から $${\zeta_1, \zeta_2, \dots, \zeta_n\in\mathbb{R}}$$ を通って $${\infty}$$ まで、実軸上を右に動かします。$${\zeta\in(\zeta_i-\epsilon, \zeta_i+\epsilon)}$$ での挙動に注目してみましょう。
$${\zeta}$$ が$${\zeta_i}$$ の左から右に移るとき、$${\zeta-\zeta_i}$$ の符号が変わって、それ以外の部分は滑らかに変化します。

$$
\begin{array}{l}\left(\frac{dz}{d\zeta}\right)_{\zeta=\zeta_i-\epsilon}=(-\epsilon)^{-\gamma_i/π}k(\zeta-\zeta_1)^{\gamma_1/π}\cdots\\\left(\frac{dz}{d\zeta}\right)_{\zeta=\zeta_i+\epsilon}=(+\epsilon)^{-\gamma_i/π}k(\zeta-\zeta_1)^{\gamma_1/π}\cdots\end{array}
$$

なので

$$
\left(\frac{dz}{d\zeta}\right)_{\zeta=\zeta_i+\epsilon}=\left(\frac{dz}{d\zeta}\right)_{\zeta=\zeta_i-\epsilon}(-1)^{\gamma_i/π}=\left(\frac{dz}{d\zeta}\right)_{\zeta=\zeta_i-\epsilon}e^{i\gamma_i}
$$

となります。
$${dz/d\zeta}$$ は $${z}$$ 平面上での方向ベクトルに相当しますので、$${\zeta}$$ が $${\zeta_i}$$ を跨ぐことで方向ベクトルの偏角が反時計回りに $${\gamma_i}$$ だけ回っていることになります。
これ故に条件文に「外角 $${\gamma_i}$$」であったり「$${\zeta}$$ 平面上の多角形」という言葉が登場します。多角形の外角の和は一般に $${2π}$$ ですから、前提条件として $${\gamma_i}$$ の和が $${2π}$$ になるよう要求されていますね。

静電場の境界値問題を解くプロトコル

静電場の境界値問題において等角写像で繋ぐべきは、導体系の形状を表す $${z}$$ 平面と、空間の電場を虚部で表す $${w}$$ 平面でした。できることなら一発で $${z \mapsto w}$$ の変換を持ってきたいところですが、そん な天才的発想が可能な頭脳を持ち合わせていない我々は、パラメーター $${ζ}$$ を一度媒介して $${z}$$ と $${w}$$ を繋ぐとい う手法をとりましょう。

ということで、$${ζ}$$ 平面から $${z}$$ 平面へのシュワルツ・クリストッフェル変換と、$${ζ}$$ 平面から $${w}$$ 平面へのシュワルツ・クリストッフェル変換とで、2 回にわたって変換を行います。

1. $${ζ \mapsto z}$$ のシュワルツ・クリストッフェル変換を導出する

   1. 境界値を与える導体表面を表す直線などを $${z}$$ 平面に描く

   2. 直線の無限遠点での交点を頂点と見做して多角形 P を作る

   3. P の外角 $${γ_1,··· ,γ_n}$$ を数え上げる

   4. P の頂点 $${z_1,··· ,z_n}$$ に対応する $${ζ_1,··· ,ζ_n}$$ を順に $${ζ}$$ 平面実軸上にとる

   5. シュワルツ・クリストッフェル変換の微分方程式を積分して解く

   6. $${ζ_1,··· ,ζ_n}$$ 近傍での $${ζ}$$ の動きと $${z_1,··· ,z_n}$$ 近傍での $${z}$$ の挙動から係数 $${k}$$ と積分定数を決定する

2. $${ζ \mapsto w}$$ のシュワルツ・クリストッフェル変換を導出する

   1. 境界における電位を虚部にもつ実軸に平行な直線を $${w}$$ 平面に描く

   2. 直線の無限遠点での交点を頂点と見做して多角形 Q を作る

   3. Q の外角 $${δ_1,··· ,δ_n}$$ を数え上げる

   4. $${ζ_1,··· ,ζ_n}$$ を順に Q の頂点 $${w_1,··· ,w_n}$$ に対応させる

   5. シュワルツ・クリストッフェル変換の微分方程式を積分して解く

   6. 対応する $${ζ}$$ 平面と $${w}$$ 平面の点での値によって係数 $${k}$$ と積分定数を決定する

3. $${ζ}$$ を消去して変換 $${f : z \mapsto w}$$ を求める

4. $${\phi(x,y)=\mathrm{Im}\:f(x,y),\; \bm{E}=−\nabla\mathrm{Im}\:f}$$

例題

習うより慣れろということで、実際に例題を使って使い方を見ていきましょう。

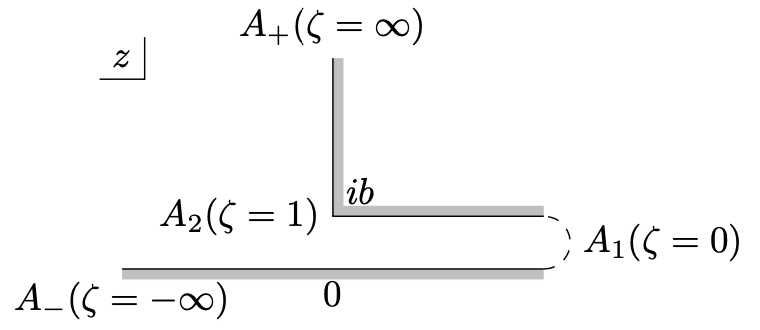
以下、解法は『詳解 電磁気学演習』に従います。等角写像法を知らずにこの手の問題が出てこようものなら、我々は手の打ちようがないですね。

手順1. ζ→zのシュワルツ・クリストッフェル変換

まずは導体系の形状を反映した$${z}$$平面への変換を探します。

はじめに$${z}$$平面における導体表面の配置を多角形で表します。平行な直線は無限遠点で交わると捉えます。

各頂点を順に$${A_1, A_2, \dots}$$ としましょう。上の図で頂点$${A_1}$$ は無限遠点です。下の直線の左側の極限の点$${A_-}$$と、上向きの直線の上側の極限の点$${A_+}$$も、無限遠点で同一点を表し、多角形の頂点をなしています。

続いて$${A_1, A_2}$$の外角を測ります。$${A_1}$$では方向ベクトルが$${\theta=0}$$の向きからから$${\theta=\pi}$$へと変わっているので、外角は$${\gamma_1=\pi}$$, $${A_2}$$では$${\gamma_2=-\pi/2}$$です。
シュワルツ・クリストッフェル変換の要件に外角の和が$${2\pi}$$になるというものがありますが、残りの外角$${3π/2}$$は無限遠点$${A_\pm}$$で適切に処理されているものとします。

次いで$${A_1, A_2}$$ に対応する点を$${\zeta}$$平面上に取ります。この点の位置は順番さえ守ればどこでも構わないので、下のように$${\zeta_1=0, \zeta_2=1}$$としましょう。

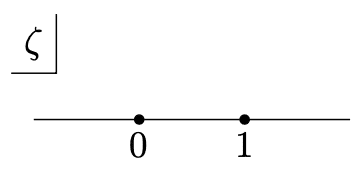
必要な道具はこれで全て揃いました。シュワルツ・クリストッフェル変換の式は

$$
\frac{dz}{d\zeta}=k_1\zeta^{-1}(\zeta-1)^{1/2}
$$

であり、積分して

$$
z=\int dz=\int d\zeta k_1\frac{(\zeta-1)^{1/2}}{\zeta}.
$$

ここで$${u=(1-\zeta)^{1/2}}$$と変数変換して

$$
\begin{array}{rcl}z&=&\displaystyle\int k_1\frac{ui}{1-u^2}2udu\\&=&\displaystyle ik_1\int\left(\frac{2}{(1-u)(1+u)}-2\right)du\\&=&\displaystyle-ik_1\left(\ln\frac{1-u}{1+u}-2u\right)+k_2\end{array}
$$

となります。

あとは定数$${k_1,k_2}$$を求めるのみです。$${A_1}$$に対応する$${\zeta_1=0}$$は変換式の特異点になっているので、図に示す経路をとって積分します。$${z}$$は$${+\infty}$$から$${+\infty+ib}$$に遷移するので、

$$
\begin{array}{rcl}\displaystyle\int_\infty^{\infty+ib}dz&=&\displaystyle\int_π^0k_1\frac{(\varepsilon e^{i\theta}-1)^{1/2}}{\varepsilon e^{i\theta}}\varepsilon e^{i\theta}id\theta\\\therefore\qquad k_1&=&ib/π.\end{array}
$$

一方$${A_2}$$は正則点なので特別の配慮は不要です、$${A_2}$$では$${u=0}$$なので、$${u}$$と$${z}$$の値を$${z}$$の表式に入れることで$${k_2=ib}$$がわかります。

以上によって$${ζ\mapsto z}$$のシュワルツ・クリストッフェル変換

$$
z=\frac{b}{π}\left(\ln\frac{1+u}{1-u}-2u\right)+ib
$$

が得られました。

手順2. ζ→wのシュワルツ・クリストッフェル変換

今度は$${ζ}$$平面から虚軸が電位を表す$${w}$$平面へのシュワルツ・クリストッフェル変換を導きます。平面の内部での多角形の取り方が異なる以外は手順1. と全く同じ方針です。

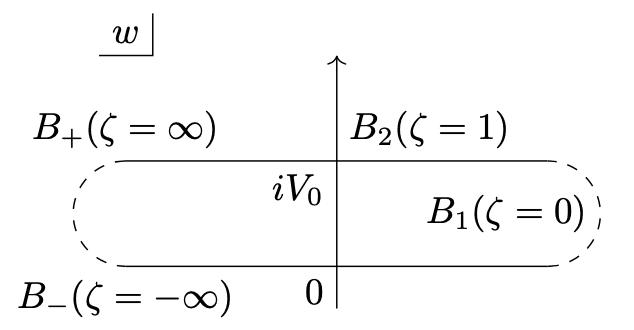
まずは図に示すように、境界部での電位を虚部に持ち、実軸に平行な直線を書いておきます。
$${A_1}$$では$${\phi=0\to V}$$と変化するので$${\zeta_1}$$に対応する$${w}$$平面での頂点$${B_1}$$は$${\infty}$$と$${\infty+iV_0}$$に対応する無限遠点です。
一方$${A_2}$$では電位の変化がないため、$${w}$$平面の上側の直線どこかしらに$${\zeta_2}$$と対応する点$${B_2}$$が置かれます。実部はなんでもいいので計算の便益を考えて$${w_2=iV_0}$$としておきましょう。

このとき多角形各頂点の外角は$${\delta_1=\pi, \delta_2=0}$$となるので、シュワルツ・クリストッフェル変換式によって

$$
\frac{dw}{d\zeta}=k_1\zeta^{-1}\qquad\therefore\quad w=k_1\ln\zeta+k_2
$$

が直ちに得られます。

ここで$${\zeta}$$の2点と$${w}$$の2点の対応から定数$${k_1, k_2}$$を決定しますが、今回は代表点にわざわざ特異点を選ぶ必要はありません。
特異点$${\zeta=\zeta_1=0}$$以前で$${z}$$は複素平面の実軸上どこかしらにあり、電位は$${0}$$です。現時点では$${w}$$の式を確定させていないので、$${w}$$平面の$${\zeta<0}$$に対応する部分と$${z}$$実軸は独立しています。
従って$${\zeta=-1}$$に対応する点が$${w}$$平面の原点にあるとして構いません。これにより特異点周りに経路をとって積分するような面倒を回避できます。

$${w}$$の表式に$${\zeta=-1, w=0}$$を代入して$${0=iπk_1+k_2}$$を得ます。一方で$${B_2}$$での挙動を$${w}$$の表式に代入すれば

$$
iV_0=i\frac{iV_0}{π}\ln|1|+k_2\qquad\therefore\quad k_2=iV_0
$$

となるので、$${k_1=-V_0/π}$$です。

以上より

$$
w=-\frac{V_0}{π}\ln\zeta+iV_0
$$

とわかりました。

手順3. パラメーターζを消去する

ここまでで$${\zeta\mapsto z}$$の変換と$${\zeta\mapsto w}$$の変換、さらに変数変換$${\zeta\mapsto u}$$の関係式が得られています。この３本と導体表面上で$${\exist\zeta\in\mathbb{R}}$$, それ以外で$${\exist\zeta\in\mathbb{C}}$$となる条件から$${\zeta}$$を消去していきます。
なお、導体表面上で実数になるように$${\zeta\mapsto z}$$の変換と$${\zeta\mapsto w}$$の変換を構成してきたので、考えなければならないのは$${\zeta\in\mathbb{C}}$$の存在条件だけです。つまり$${\zeta}$$を代入、消去すればいいですね。

まず$${\zeta\mapsto w}$$の変換から直ちに

$$
\zeta=\exp\left(iπ-\frac{wπ}{V_0}\right)=-e^{-(π/V_0)w}
$$

が成り立ちます。変数変換$${\zeta\mapsto u}$$の関係式に入れると

$$
u=\sqrt{1+e^{-(π/V_0)w}}.
$$

これを$${\zeta\mapsto z}$$の変換に入れて

$$
z=\frac{b}{π}\ln\left(\frac{1+\sqrt{1+e^{-(π/V_0)w}}}{1-\sqrt{1+e^{-(π/V_0)w}}}-2\sqrt{1+e^{-(π/V_0)w}}\right)+ib
$$

となります。

原理的にはこれを$${w=\cdots}$$の形式に直して虚部を取れば平面内の電位が得られ、さらに勾配をとって電場が決定します。

注意

以上の例題からも分かる通り、境界条件を与える導体が複数ある場合にシュワルツ・クリストッフェル変換を使うには、導体が全て無限遠まで続いていることが要求されます。でなければ$${z}$$平面において導体を多角形で繋ぐ操作が不可能です。この手の問題については他の方法を試す必要があります。